Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение рациональных функций
Определение. Рациональной функцией называется отношение двух многочленов
где Примеры: 1) Определение. Если степень числителя выше или совпадает со степенью знаменателя ( Примеры: 1-я и 2-я функции – неправильные дроби, 3-я функция – правильная дробь. Интегрирование дробно-рациональных функций в конечном итоге сводится к интегрированию правильных дробей, так как неправильную дробь выделением целой части можно представить в виде суммы многочлена и правильной дроби. Примеры: 1)
2) Выделяем целую часть делением в столбик, в результате чего получаем:
Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей. Определение. Правильные рациональные дроби вида I. II. III. IV. называются простейшими дробями I, II, III, IV типов. Никаких других простейших правильных дробей не существует.
Интегрирование простейших правильных дробей Рассмотрим методы интегрирования простейших дробей I, II, III типов. I. II. III.
(подставляем в числитель производную знаменателя Тогда
Пример:
В данном случае производная знаменателя равна
Интегрирование правильных дробей Рассмотрим правильную дробь
где
где показатели у знаменателей последовательно уменьшаются от
Методы нахождения неопределённых коэффициентов
1) Метод частных значений:
Тогда Придаём x переменной определённые значения (корни знаменателя) и находим коэффициенты A и B:
В качестве частных значений берём корни знаменателя, получаем:
2) Метод сравнения коэффициентов:
Получаем Даём x значение, равное действительному корню знаменателя:
Сравниваем коэффициенты при одинаковых степенях x: при при
Получаем
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.244.44 (0.009 с.) |
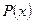 и
и 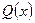 :
: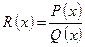 ,
,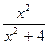 ; 2)
; 2) 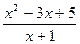 ; 3)
; 3)  .
.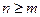 ), то дробь
), то дробь 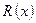 называется неправильной, в противном случае (
называется неправильной, в противном случае ( ) дробь
) дробь 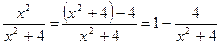
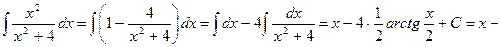
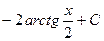

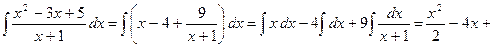

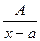

 (корни знаменателя комплексные, т.е.
(корни знаменателя комплексные, т.е.  )
) , (
, (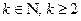 , корни знаменателя комплексные)
, корни знаменателя комплексные)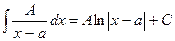
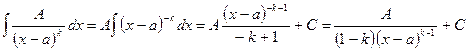
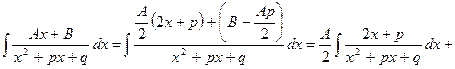

 и в знаменателе второй дроби выделяем полный квадрат
и в знаменателе второй дроби выделяем полный квадрат 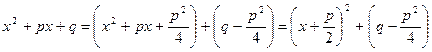 , где
, где 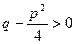 , так как
, так как 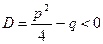 )
)
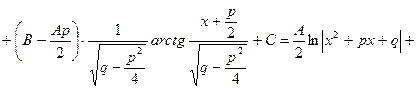
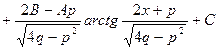
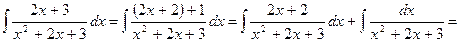
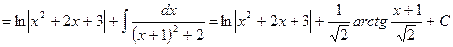
 .
.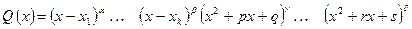 ,
,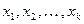 - действительные корни многочлена
- действительные корни многочлена 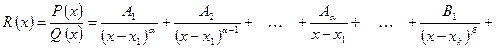

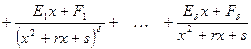 ,
,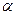 до 1,
до 1, 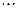 , от
, от 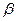 до 1, от
до 1, от  до 1,
до 1, 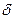 до 1, а
до 1, а  ,
,  - неопределённые коэффициенты.
- неопределённые коэффициенты.
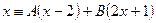 .
.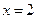 :
: 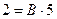 ,
, 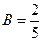
 :
: 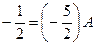 ,
, 
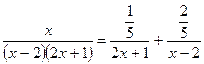


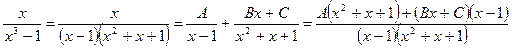
 .
.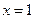 :
: 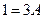 ,
, 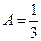
 :
:  .
.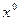 :
:  .
.