
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные различных порядков
Пусть на некотором множестве
Аналогично, если существует производная от второй производной, то она называется производной третьего порядка или третьей производной и обозначается через
Производной n-го порядка от функции
Производные четвёртого, пятого и высших порядков обозначаются Примеры: 1) Найдите Решение. 2) Найдите Решение. Докажем формулу для Для Предположим, что формула верна для Докажем, что формула верна для
Таким образом, формула верна для любого Для производных n-го порядка справедливы формулы:
а также формула Лейбница:
Тема 8. ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Теорема о корнях производной (теорема Ролля)
Теорема Ролля. Если функция 1) непрерывна на отрезке 2) дифференцируема на интервале 3) то существует, по крайней мере, одна точка
Геометрическая иллюстрация. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках
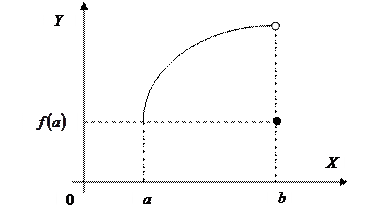
Замечание 1. Доказанная теорема остается справедливой и для такой дифференцируемой функции, которая на концах отрезка Замечание 2. Все три условия теоремы необходимы. 1) Нарушено первое условие, функция
2) Нарушено второе условие теоремы,
3) Нарушено третье условие теоремы,
Пример: Проверим, применима ли теорема Ролля к функции Функция 1) непрерывна на отрезке
2) дифференцируема на интервале 3) Тогда существует точка В качестве точки c можно выбрать также
Теорема о конечных приращениях (теорема Лагранжа)
Теорема Лагранжа. Если функция 1) непрерывна на отрезке 2) дифференцируема на интервале то существует, по крайней мере, одна точка
Геометрическая иллюстрация. Из
Пример: Проверьте, применима ли теорема Лагранжа к функции Решение. Функция 1) непрерывна на отрезке 2) дифференцируема на интервале Тогда существует точка Находим значения По формуле (1) получаем:
Находим корни квадратного уравнения
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.29.145 (0.013 с.) |
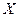 определена дифференцируемая функция
определена дифференцируемая функция 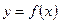 . Производная
. Производная 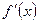 этой функции также является функцией от
этой функции также является функцией от 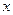 . Следовательно, можно говорить о производной этой функции, т.е. о производной от первой производной. Если она существует, то её называют производной второго порядка функции
. Следовательно, можно говорить о производной этой функции, т.е. о производной от первой производной. Если она существует, то её называют производной второго порядка функции 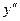 или
или 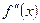 :
: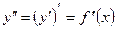 .
.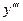 или
или 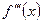 :
: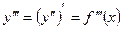 .
.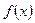 называется производная первого порядка от производной
называется производная первого порядка от производной 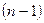 -го порядка и обозначается символом
-го порядка и обозначается символом 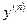 или
или 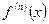 :
: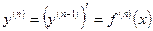 .
.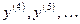 или
или 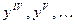 .
.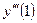 для функции
для функции 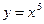 .
.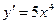 ,
, 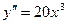 ,
, 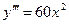 ,
, 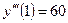 .
.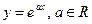 .
.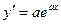 ,
, 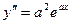 ,
, 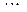 ,
, 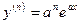 .
.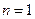 получаем
получаем 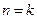 , т.е.
, т.е. 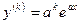 .
.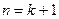 :
: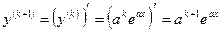 .
.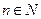 .
.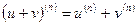 ,
,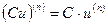 ,
,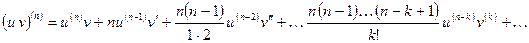
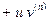 .
.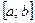 ;
;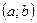 ;
;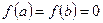 ;
;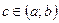 , для которой
, для которой 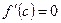 .
.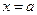 и
и 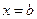 , то на этой кривой найдётся, по крайней мере, одна точка
, то на этой кривой найдётся, по крайней мере, одна точка 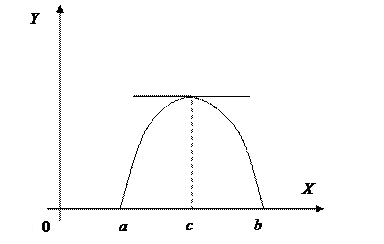
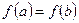 .
.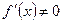 для всех
для всех  .
.
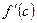 не существует,
не существует, 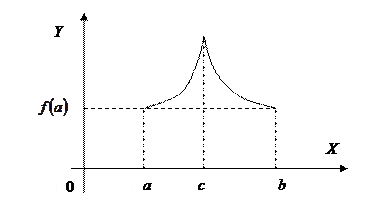
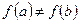 ,
, 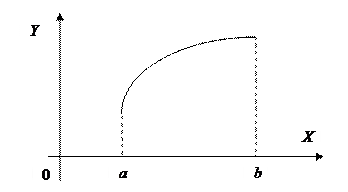
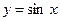 на отрезке
на отрезке 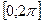 . Найдём точку c, в которой
. Найдём точку c, в которой 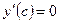 .
.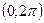 ,
, 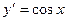 ;
;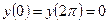 .
.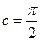 , такая, что
, такая, что 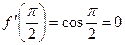 .
.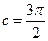 .
.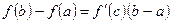 . (1)
. (1)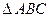 :
: 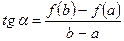 . Таким образом, если во всех точках дуги AB существует касательная, то на этой дуге найдётся точка C между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.
. Таким образом, если во всех точках дуги AB существует касательная, то на этой дуге найдётся точка C между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.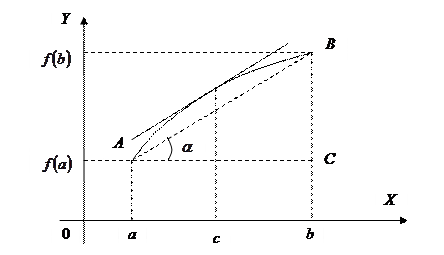
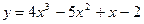 на отрезке
на отрезке 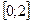 . Если окажется, что теорема применима, найдите точку c, в которой выполняется равенство (1).
. Если окажется, что теорема применима, найдите точку c, в которой выполняется равенство (1).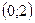 .
.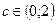 , такая, что выполняется равенство (1).
, такая, что выполняется равенство (1).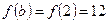 ,
, 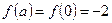 ,
, 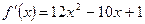 ,
, 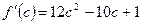 .
.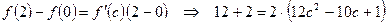
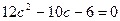 , т.е.
, т.е. 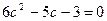 . Получаем
. Получаем 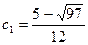 ,
, 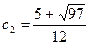 , где
, где 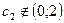 . Таким образом,
. Таким образом, 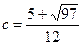 .
.


