
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение бесконечно малых функций
Определение 1. Пусть функции Если Если Если Если Примеры: 1) 2) 3) 4) Определение 2. Функцию функцию
функцию Определение 3. Если (обозначение Теорема. Пусть функции Доказательство:
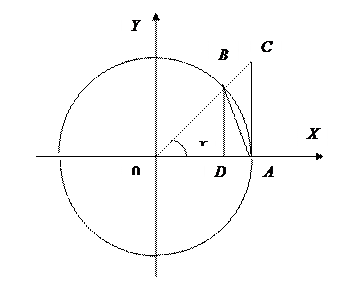
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Пределы Теорема 1. Предел
Доказательство: Рассмотрим единичную окружность, пусть
Получаем неравенство Поделим последнее неравенство на
Отсюда следует
Так как Так как Примеры: 1) 2)
3) замена: 4) замена:
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Теорема. Функция
Обозначим
Таким образом,
Некоторые примеры пределов функций. 1) Доказательство:
Следствие 1. Пусть 2) Доказательство:
Следствие 2. Пусть 3) Доказательство:
По следствию 1 Следствие 3.
Тема 5. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
ОДНОСТОРОННИЕ ПРЕДЕЛЫ
Если при нахождении предела рассматривать значения x только слева от точки a, то такой предел называется левым или левосторонним и обозначается
а если рассматривать значения x только справа от точки a, то такой предел называется правым или правосторонним и обозначается
Из этих определений следует, что если существует предел
то существуют и односторонние пределы, причём
Верно и обратное утверждение: если имеет место (2), то имеет место и (1). Пример: Найти односторонние пределы функции
НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.184 (0.019 с.) |
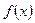 и
и 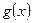 бесконечно малые при
бесконечно малые при  .
.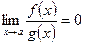 , то
, то 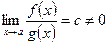 , то
, то 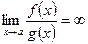 ,то
,то 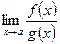 не существует, то
не существует, то 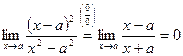
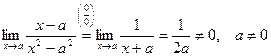
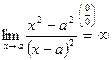 (вследствие примера 1)
(вследствие примера 1)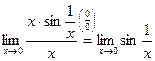 - не существует
- не существует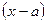 при
при 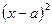 при
при 
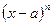 при
при 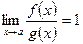 , где
, где 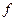 ~
~ 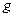 )
) ,
,  ,
, 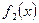 ,
, 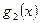 бесконечно малые при
бесконечно малые при 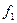 ~
~ 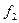 ,
, 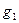 ~
~ 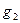 при
при 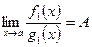 . Тогда
. Тогда 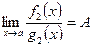 .
.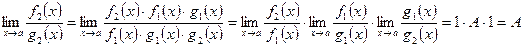
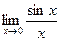 и
и 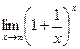 принято называть первым и вторым замечательными пределами ввиду их важности в дальнейших приложениях.
принято называть первым и вторым замечательными пределами ввиду их важности в дальнейших приложениях.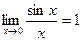
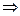
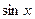 ~
~ 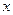 при
при 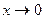
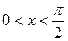 ).
).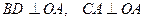 ,
,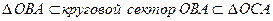 ,
,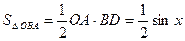 ,
,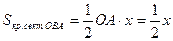 ,
,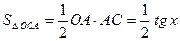 .
.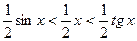 , т.е.
, т.е. 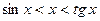 .
.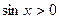
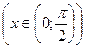 :
: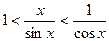 .
.
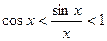 . (*)
. (*) и
и 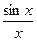 – чётные функции, то неравенство (*) выполняется для
– чётные функции, то неравенство (*) выполняется для 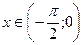 , т.е. (*) имеет место в проколотой окрестности
, т.е. (*) имеет место в проколотой окрестности 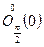 .
.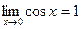 ,
, 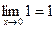 и выполняется (*), то
и выполняется (*), то 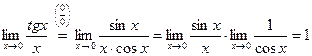
 ~
~ 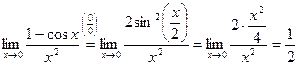
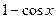 ~
~ 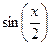 ~
~  при
при 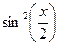 ~
~ 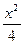 при
при 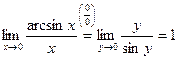
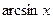 ~
~  ,
, 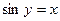 ,
, 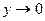
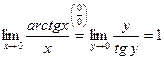
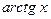 ~
~ 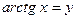 ,
, 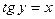 ,
, 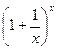 стремится при
стремится при 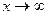 к пределу e:
к пределу e: (неопределённость
(неопределённость 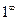 ).
).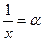 ,
, 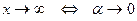 . Тогда
. Тогда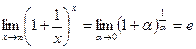 .
.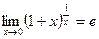 .
.
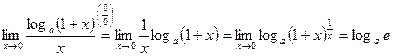
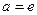 , тогда
, тогда 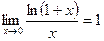 , т.е.
, т.е. 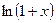 ~
~ 
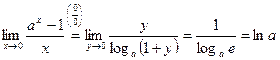
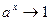 , замена:
, замена: 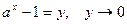 ,
, 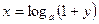
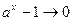
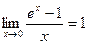 , т.е.
, т.е. 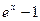 ~
~ 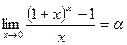
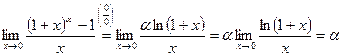
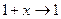 ,
,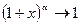 ,
,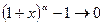
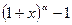 ~
~ 
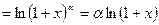 при
при 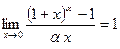 , т.е.
, т.е. 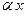 при
при 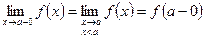 .
.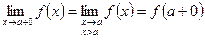 .
.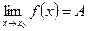 , (1)
, (1)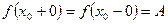 . (2)
. (2)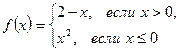 в точке
в точке 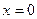 . Существует ли у этой функции предел при
. Существует ли у этой функции предел при 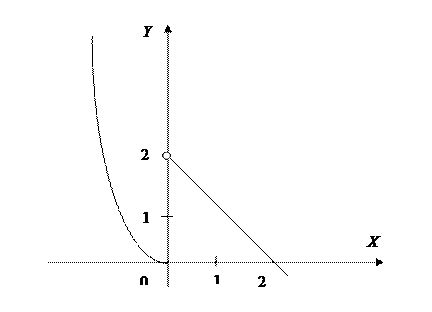
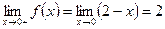 ;
;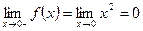 ;
;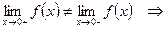
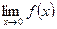 - не существует.
- не существует.


