
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Числовые последовательности. Предел последовательности
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение. Бесконечной числовой последовательностью называется числовая функция Число Способы задания числовой последовательности: 1. Задание функции
Формулу (1) называют формулой общего члена последовательности. По этой формуле можно вычислить любой член последовательности. Примеры: 1) Тогда Последовательность имеет вид: 2) Тогда Последовательность имеет вид: 0; 1; 0; 1; 0; 1; Последовательность, у которой все члены принимают равные между собой значения, называется постоянной последовательностью. 2. Рекуррентный способ задания последовательности, который состоит в том, что указывается правило, позволяющее вычислить общий член последовательности через предыдущие члены, а также задаются несколько начальных членов последовательности. Формула, позволяющая вычислить общий член последовательности через предыдущие члены, называется рекуррентным соотношением. Пример: Тогда Последовательность имеет вид: 1; 0; -1; -2; -3; -4;…. 3. Последовательность задаётся словесно, то есть описанием её членов.
ОГРАНИЧЕННЫЕ И МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение 1. Последовательность Примеры: 1) Последовательность имеет вид: Так как 2) Последовательность имеет вид: -1; 1; -1; 1; -1; 1; …; Так как Определение 2. Последовательность Определение 3. Последовательность
Все эти последовательности называются монотонными последовательностями. Пример: Последовательность задана формулой
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ Пример: Рассмотрим последовательность Зафиксируем число
Для произвольного числа
равносильно неравенству Определение 1. Пусть задана числовая последовательность В этом случае пишут Иначе,
Определение 2. Последовательность, имеющая предел, называется сходящейся, а не имеющая предела – расходящейся. Теорема 1. Если последовательность имеет предел, то она ограничена. Доказательство: Пусть
Таким образом, Теорема 2. Всякая сходящаяся последовательность имеет только один предел. Доказательство: Используем метод от противного. Пусть последовательность Возьмём
Отсюда С другой стороны,
Отсюда Получаем
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.8.82 (0.01 с.) |
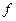 , определённая на множестве всех натуральных чисел
, определённая на множестве всех натуральных чисел 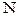 . Её обозначают
. Её обозначают 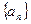 или
или 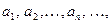 где
где 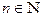 .
.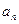 называется n – м (общим) членом последовательности, а число n – номером члена
называется n – м (общим) членом последовательности, а число n – номером члена  (1)
(1)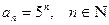 .
.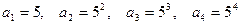 и т.д.
и т.д.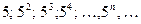 .
.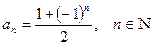 .
.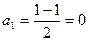 ,
, 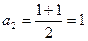 ,
,  ,
, 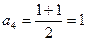 и т.д.
и т.д.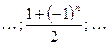 .
.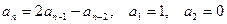 .
.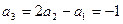 ;
;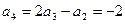 ;
;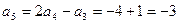 ;
;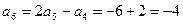 ;
;
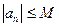 (то есть
(то есть  ). В противном случае последовательность называется неограниченной.
). В противном случае последовательность называется неограниченной.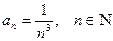 .
.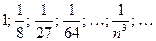 .
.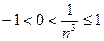 , то
, то 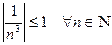 . Тогда по определению 1 последовательность
. Тогда по определению 1 последовательность 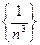 ограничена.
ограничена. .
. ; ….
; ….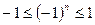 , то
, то 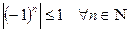 . Тогда по определению 1 последовательность
. Тогда по определению 1 последовательность 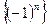 ограничена.
ограничена.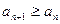 . Если же
. Если же 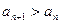 , то последовательность
, то последовательность 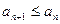 . Если же
. Если же 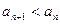 , то последовательность
, то последовательность 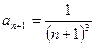 . Так как
. Так как 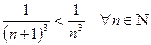 , т.е.
, т.е. 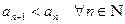 , то последовательность
, то последовательность 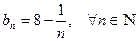 . Последовательность имеет вид:
. Последовательность имеет вид: 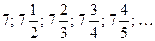 . Таким образом,
. Таким образом, 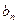 с возрастанием номера n приближается к 8. Придадим этому утверждению точную математическую формулировку.
с возрастанием номера n приближается к 8. Придадим этому утверждению точную математическую формулировку.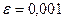 и поставим вопрос, каким должно быть n, чтобы модуль
и поставим вопрос, каким должно быть n, чтобы модуль 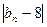 был меньше 0,001?
был меньше 0,001?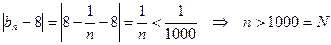
 неравенство
неравенство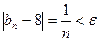 (1)
(1)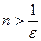 . Так как
. Так как  , где
, где 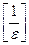 – целая часть числа
– целая часть числа 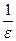 . В этом случае говорят, что предел последовательности
. В этом случае говорят, что предел последовательности 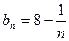 равен 8 и пишут
равен 8 и пишут 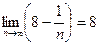 .
.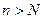 выполняется неравенство
выполняется неравенство 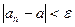 .
.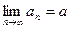 .
.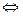
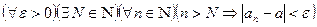 .
.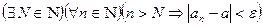 .
.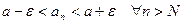 . Вне интервала
. Вне интервала 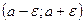 могут оказаться лишь N первых членов последовательности:
могут оказаться лишь N первых членов последовательности: 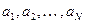 . Среди чисел
. Среди чисел 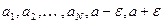 найдём наименьшее и наибольшее и обозначим их соответственно m и M. Тогда
найдём наименьшее и наибольшее и обозначим их соответственно m и M. Тогда  . Отсюда последовательность
. Отсюда последовательность 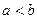 ).
).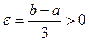 , отсюда
, отсюда 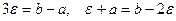 . Тогда справедливо неравенство:
. Тогда справедливо неравенство: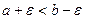 . (2)
. (2)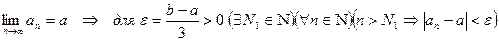
 , в частности,
, в частности,  .
.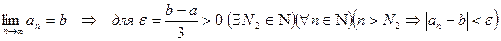 .
.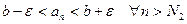 , в частности,
, в частности, 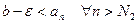 .
.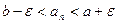 для
для 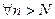 , где
, где 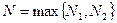 , что противоречит неравенству (2). Теорема доказана.
, что противоречит неравенству (2). Теорема доказана.


