
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о пределах последовательностей, связанные с арифметическими действиями
Теорема 1 (о пределе суммы). Если последовательности
Доказательство: Пусть
где
где
Теорема 2 (о пределе произведения). Если последовательности
Доказательство: Пусть
где
где
Следствие 1. Постоянный множитель можно выносить за знак предела:
Доказательство: Пусть
Следствие 2. Если последовательности
Доказательство: самостоятельно. Теорема 3 (о пределе частного). Если последовательности
Доказательство: Пусть
где
Примеры: 1) 2) БЕСКОНЕЧНО БОЛЬШИЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение. Последовательность
Теорема. Если последовательность Доказательство: 1)
Зафиксируем
Следовательно, 2)
Положим
Таким образом, Пример:
Последовательность
Тема 3. ПРЕДЕЛ ФУНКЦИИ
Определение 1. Пусть функция Определение 2. Назовём окрестностью точки c любой интервал
Определение 3. Число A называется пределом функции Обозначение:
Графическая иллюстрация.
Так как из неравенства Примеры: 1) Доказать, что Фиксируем 2) Доказать, что Фиксируем
тогда Найдём Определение 4. Число A называется пределом функции
Предел функции Справедлива следующая теорема: Теорема. Функция не может иметь двух разных пределов в точке.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.175.164 (0.015 с.) |
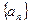 и
и 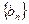 сходятся, то их сумма
сходятся, то их сумма 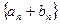 тоже сходится и предел суммы равен сумме пределов:
тоже сходится и предел суммы равен сумме пределов: .
.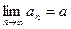 ,
,  . Тогда по рассмотренной в предыдущем пункте теореме 3 имеем
. Тогда по рассмотренной в предыдущем пункте теореме 3 имеем ,
, 
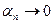 и
и  при
при 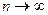 . Следовательно,
. Следовательно,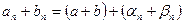 ,
, при
при 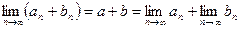 .
.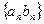 сходится и предел произведения равен произведению пределов:
сходится и предел произведения равен произведению пределов: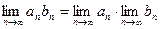 .
. ,
, при
при  .
.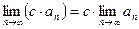 .
. - постоянная, следовательно,
- постоянная, следовательно,  . Тогда по теореме о пределе произведения получаем:
. Тогда по теореме о пределе произведения получаем: .
.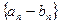 тоже сходится и предел разности равен разности пределов:
тоже сходится и предел разности равен разности пределов: .
. и
и  , то их частное
, то их частное 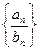 тоже сходится и предел частного равен частному пределов:
тоже сходится и предел частного равен частному пределов: .
. . Тогда
. Тогда 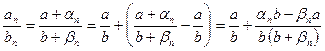 ,
, при
при  .
.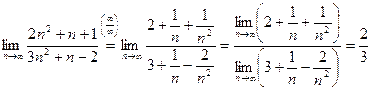

 найдётся такой номер
найдётся такой номер 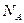 , что для всех
, что для всех  верно неравенство
верно неравенство 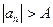 . В этом случае пишут
. В этом случае пишут 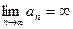 .
.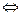
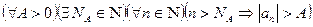
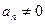 , бесконечно большая, то последовательность
, бесконечно большая, то последовательность  бесконечно малая. Верно обратное утверждение: если последовательность
бесконечно малая. Верно обратное утверждение: если последовательность 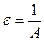 :
: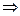
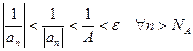 ,
,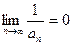 , т.е. последовательность
, т.е. последовательность 
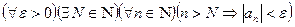
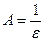 :
:
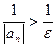 .
. для любого
для любого 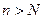 . Отсюда
. Отсюда 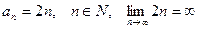
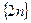 – бесконечно большая, тогда последовательность
– бесконечно большая, тогда последовательность  – бесконечно малая и
– бесконечно малая и  .
.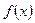 определена в некоторой окрестности точки a, кроме, может быть, самой точки a. Число A называется пределом функции
определена в некоторой окрестности точки a, кроме, может быть, самой точки a. Число A называется пределом функции 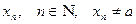 , сходящейся к a (т.е.
, сходящейся к a (т.е. 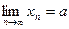 ), последовательность соответствующих значений функции
), последовательность соответствующих значений функции 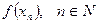 сходится к числу A. В этом случае пишут
сходится к числу A. В этом случае пишут 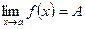 или
или 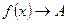 при
при  .
.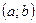 , содержащий c, а
, содержащий c, а 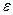 – окрестностью точки c интервал
– окрестностью точки c интервал 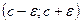 , где
, где  .
.
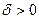 , что для всех
, что для всех 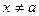 , удовлетворяющих условию
, удовлетворяющих условию 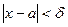 , имеет место неравенство
, имеет место неравенство 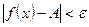 .
.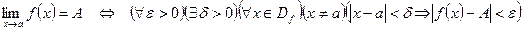
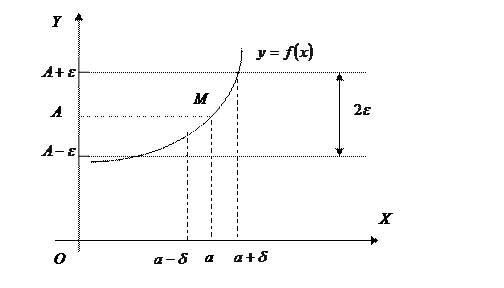
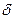 , точки графика функции
, точки графика функции 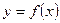 лежат внутри полосы шириной
лежат внутри полосы шириной 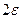 , ограниченной прямыми
, ограниченной прямыми 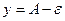 и
и 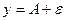 .
.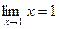 .
.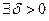 , такое, что для
, такое, что для 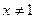 из условия
из условия 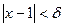 следует
следует 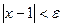 .Очевидно,
.Очевидно, 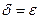 .
.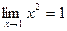 .
.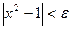 .
.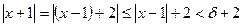 ,
,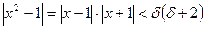 , отсюда
, отсюда 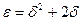 .
.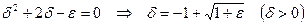 .
.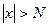 имеет место неравенство
имеет место неравенство 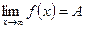 .
.
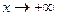 (
(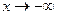 ) определяется аналогично пределу функции
) определяется аналогично пределу функции 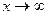 , только в самой формулировке определения предела функции
, только в самой формулировке определения предела функции 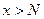 (
(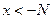 ).
).


