Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ РОДИОНОВА Ольга Владимировна ⇐ ПредыдущаяСтр 2 из 17Следующая ⇒ СИТНИКОВА Людмила Дмитриевна СОРОКИНА Наталия Владимировна Печатается с авторского оригинал-макета. Подписано в печать 24.11.2019. Формат 60´90/16. Бумага офсетная. Печать трафаретная. Усл. печ. л. 5. Уч.-изд. л. 5,95. Тираж 100 экз. ООО «Тульское производственное полиграфическое объединение». 300600, Тула, ул. Каминского, 33.   © Сост.: Н.М. Исаева, Н.В.Мыслик, Е.М. Рарова, О. В. Родионова, Л.Д. Ситникова, Н.В. Сорокина, 2019   СОДЕРЖАНИЕ   РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ 44 тема 1. ФУНКЦИЯ 44 тема 2. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 57 тема 3. ПРЕДЕЛ ФУНКЦИИ 65 тема 4. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ 68 тема 5. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ 72       РАЗДЕЛ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 2 тема 6. ПРОИЗВОДНАЯ ФУНКЦИИ. ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 2 тема 7. ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ПРОИЗВОДНЫЕ РАЗЛИЧНЫХ ПОРЯДКОВ 7 тема 8. ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 11 тема 9. ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ 15       РАЗДЕЛ 3. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 23 тема 10. ОПРЕДЕЛЕНИЕ И СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 23 тема 11. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 27 тема 12. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ И ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 31       РАЗДЕЛ 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 34 тема 13. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 34 тема 14. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 39 тема 15. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 43       РАЗДЕЛ 5. варианты контрольных работ 49       СПИСОК ЛИТЕРАТУРЫ

51

 

РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ

 

Тема 1. ФУНКЦИЯ

 

Определение 1. Функцией (или отображением) из множества X в множество Y будем называть правило f, по которому каждому элементу из множества X соответствует единственный элемент из множества Y.

Элемент 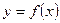 называется образом элемента x при отображении f.

Определение 2. Если 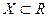, , 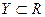то функцию f называют действительной функцией действительной переменной.

Множество 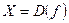 называют областью определения функции f, множество  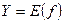называют множеством значений функции f,  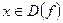называют аргументом функции f, а  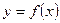– значением функции f в точке x ().

 

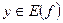СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ

1) аналитический;

2) графический;

3) табличный;

4) описательный.

1) аналитический способ: наиболее часто функцию задают с помощью формулы (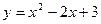, 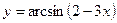). Под областью определения в этом случае естественно понимать множество всех значений x, для которых определено значение выражения .

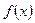Пример:

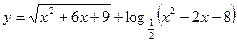
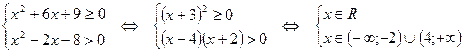
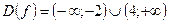
2) графический способ:

Определение. Графиком функции 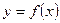 называется множество  точек координатной плоскости.

Замечание. Некоторое множество координатной плоскости является графиком некоторой функции, если это множество имеет не более одной общей точки с любой прямой, параллельной оси OY.

Наиболее важными при рассмотрении графика функции являются две задачи:

1) функция f задана аналитически. Требуется исследовать свойства этой функции и построить её график (часто это эскиз графика).

Пример:

1) 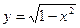 – можно построить график точно;

2) 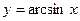 – можно построить эскиз графика.

2) функция f задана графически. Требуется определить основные свойства функции, т.е. «прочитать» график.

3) табличный способ:

 

x	1	2	3	4
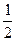
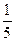
y			1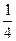

 

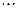
4) описательный способ:

В случаях, когда формулу, по которой каждому 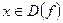 ставится в соответствие 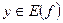, записать трудно (или невозможно), пользуются словесным описанием способа, задающего функцию.

Пример:

Каждому действительному числу x ставится в соответствие наибольшее целое число, не превосходящее x. Эта функция называется целой частью x и обозначается .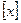

 

НЕКОТОРЫЕ КЛАССЫ ФУНКЦИЙ

 

1) монотонные функции;

2) ограниченные и неограниченные функции;

3) чётные и нечётные функции;

4) периодические функции.

1) монотонные функции:

Определение 1. Функция 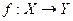 называется возрастающей на множестве 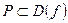, если для любых  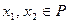из условия  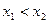следует .

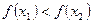Определение 2. Функция 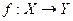 называется убывающей на множестве 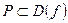, если для любых  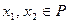из условия  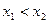следует .

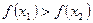Возрастающие и убывающие функции называются строго монотонными.

Определение 3. Функция 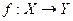 называется неубывающей на множестве 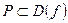, если для любых  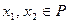из условия  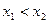следует .

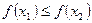Определение 4. Функция 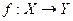 называется невозрастающей на множестве 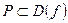, если для любых  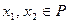из условия  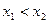следует .

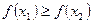Функции всех четырёх классов называются монотонными.

Определение 5. Функция 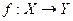 называется кусочно-монотонной, если её область определения  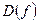можно разбить на конечное множество промежутков, на каждом из которых функция монотонна.

Примеры: ,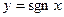

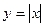
2) ограниченные и неограниченные функции:

Определение 1. Функция 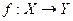 называется ограниченной сверху на множестве 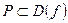, если множество  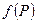является ограниченным сверху, то есть .

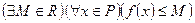Определение 2. Функция 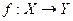 называется ограниченной снизу на множестве 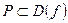, если множество  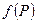является ограниченным снизу, то есть .

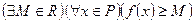Определение 3. Функция 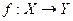 называется ограниченной на множестве 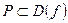, если множество  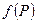ограничено, то есть .

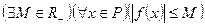В противном случае функция называется неограниченной.

3) чётные и нечётные функции:

Определение 1. Функция 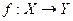 называется чётной, если:

1) 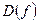 симметрична относительно начала координат, то есть если 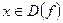, то ;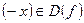

2) .

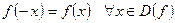Определение 2. Функция 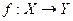 называется нечётной, если:

1) 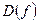 симметрична относительно начала координат, то есть если 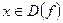, то ;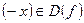

2) .

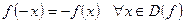4) периодические функции:

Определение. Функция 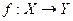 называется периодической с периодом 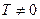, если:

1) ;

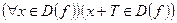2) .

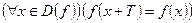Если 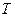 – период функции 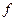, то для любого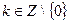 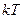 - тоже период. Наибольшего периода не существует. Но не всякая функция имеет наименьший положительный период.

Пример:

Функция Дирихле не имеет наименьшего положительного периода, так как 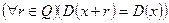, отсюда любое  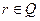есть период функции 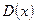, но наименьшего положительного рационального числа не существует.