Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функций, непрерывных в точке
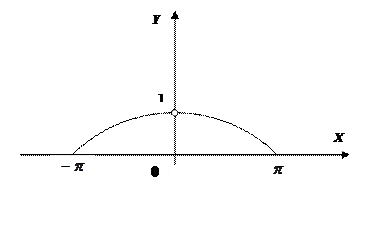
Определение 1. Функция Пример: Функция Согласно данному определению, непрерывность функции 1) функция 2) существуют 3) 4) Если хотя бы одно из условий 1) - 4) не выполняется, то функция Классификация точек разрыва 1. точки устранимого разрыва; 2. точки разрыва первого рода (скачки); 3. точки разрыва второго рода. 1. Примеры: 1)
Продолжим функцию до непрерывности:
2)
Переопределим значение функции в точке Определение 2. Точка 2. Определение 3. Точка Пример:
следовательно, 3. Определение 4. Точка Примеры: 1)
Рассмотрим точку
следовательно, 2)
3)
Свойства функций, непрерывных в точке. Теорема 1. Сумма (разность) конечного числа функций, непрерывных в точке Теорема 2. Произведение конечного числа функций, непрерывных в точке Теорема 3. Частное двух функций, непрерывных в точке
Пример: Функция
РАЗДЕЛ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Тема 6. ПРОИЗВОДНАЯ ФУНКЦИИ. ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Определение производной
Определение производной. Пусть задана функция
называется производной функции
Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке. Функция Обозначение производной функции Если ввести приращение аргумента
Так как
Примеры: 1) Дана функция Решение. а)
б) в) Таким образом, 2) Найдите производную функции Решение. а)
б) в)
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.203 (0.014 с.) |
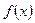 называется непрерывной в точке
называется непрерывной в точке 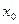 , если она задана в этой точке и в некоторой её окрестности и если
, если она задана в этой точке и в некоторой её окрестности и если 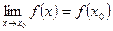 .
.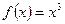 непрерывна в любой точке
непрерывна в любой точке 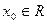 и поэтому
и поэтому  , например,
, например, 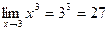 .
.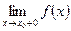 и
и 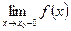 ;
; ;
;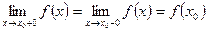 .
.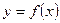 будет разрывной в точке
будет разрывной в точке 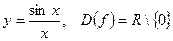
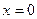 - точка разрыва,
- точка разрыва,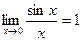 , функция не определена в точке
, функция не определена в точке 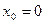 .
.
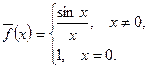
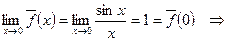 функция
функция 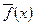 непрерывна в точке
непрерывна в точке 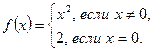
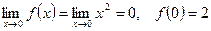 , тогда точка
, тогда точка 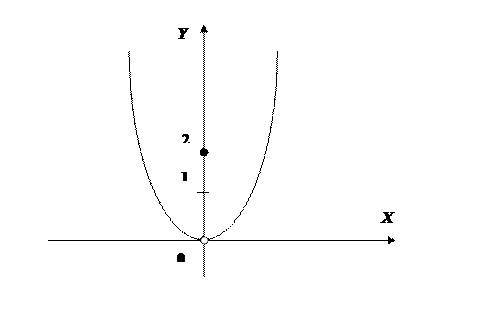
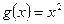 .
. , но
, но 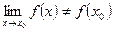 или значение функции
или значение функции 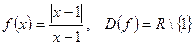
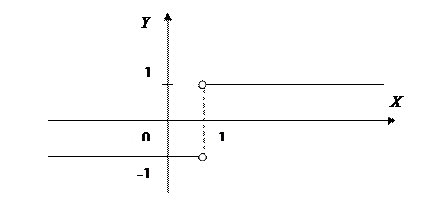
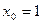 - точка разрыва,
- точка разрыва,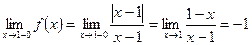 ,
,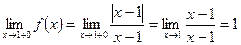 ,
,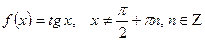
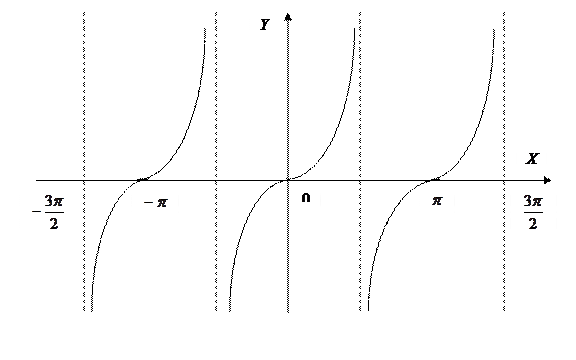
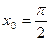 .
. ,
, 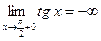 ,
,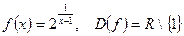
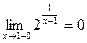 ,
, 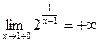
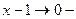 ,
, 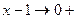 ,
,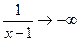 ,
, 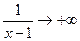 ,
,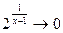 ,
, 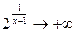
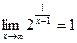 , следовательно, прямая
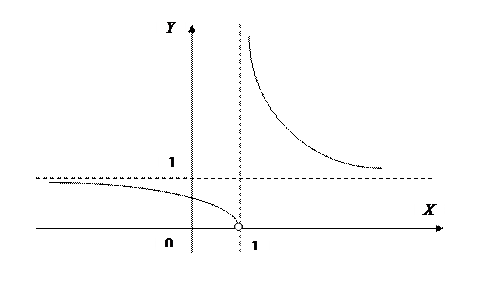
, следовательно, прямая 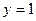 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  .
.
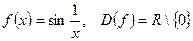
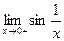 - не существует;
- не существует;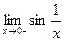 - не существует.
- не существует. непрерывна в любой точке
непрерывна в любой точке 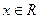 как произведение двух непрерывных функций.
как произведение двух непрерывных функций.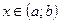 и пусть
и пусть 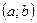 . Предел
. Предел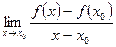
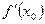 (если последний предел существует). Таким образом, по определению,
(если последний предел существует). Таким образом, по определению,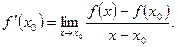
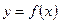 :
: 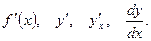
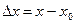 и приращение функции
и приращение функции 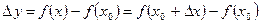 , определение производной запишется в виде
, определение производной запишется в виде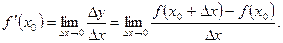

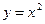 , найдите её производную.
, найдите её производную.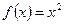 ,
, 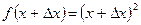 ,
,
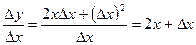

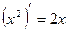 .
.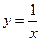 .
.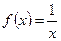 ,
,  ,
,