Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность дифференцируемой функции
Докажем необходимое условие существования производной. Теорема. Если функция Доказательство: По определению производной Тогда по свойству предела функции получаем
Находим предел функции
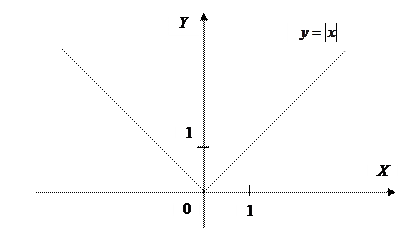
Отсюда по определению функция Замечания: 1) В точках разрыва функция не имеет производной. 2) Непрерывность функции в точке не является достаточным условием существования производной этой функции в рассматриваемой точке, т.е. из непрерывности функции в точке не следует её дифференцируемость в этой точке. Пример: Пусть
Функция Найдём Рассмотрим односторонние пределы:
Отсюда
Производная суммы, разности, произведения и частного функций
Теорема 1. Если функции
т.е. производная суммы (разности) функций равна сумме (разности) производных этих функций. Теорема 2. Если функции
Следствие. Постоянный множитель можно выносить за знак производной, т.е. Теорема 3. Если функции
Производные некоторых элементарных функций 1. 2. 3. 4. 5. 6. 7. 8. Пример: Найдите производную функции Решение. По теореме 1 и следствию из теоремы 2 получаем:
Пример: Найдите производную функции Решение. По теореме 3 получаем:
Производная сложной функции
Пусть задана сложная функция
или Теорема. Если функция
где вместо u должно быть подставлено выражение Коротко,
т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x. Пример: Дана функция Решение. Введем промежуточный аргумент u:
Тогда
Следствие. Если функция
Пример: Дана функция Решение. Пусть
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.69.143 (0.007 с.) |
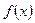 имеет производную в точке
имеет производную в точке 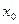 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.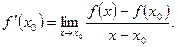
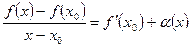 , где
, где 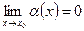 . Отсюда
. Отсюда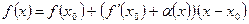 .
.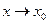 :
: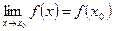 .
.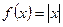 ,
, 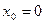 .
.
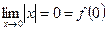 .
.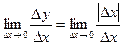 .
.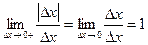 ;
; 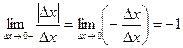 .
.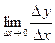 не существует, т.е. функция
не существует, т.е. функция  и
и 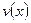 дифференцируемы на некотором интервале, то на этом интервале
дифференцируемы на некотором интервале, то на этом интервале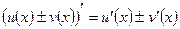
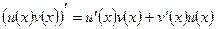 .
.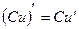 , где
, где 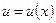 - дифференцируемая функция.
- дифференцируемая функция.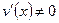 для любого x из этого интервала, то
для любого x из этого интервала, то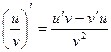 .
.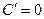 9.
9. 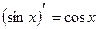
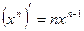 10.
10. 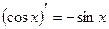
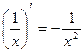 11.
11. 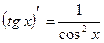
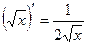 12.
12. 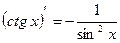
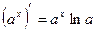 13.
13. 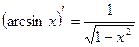
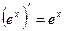 14.
14. 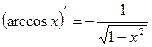
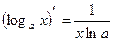 15.
15. 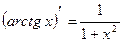
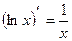 16.
16. 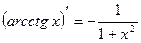
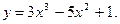
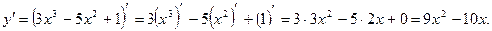
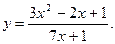
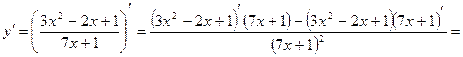
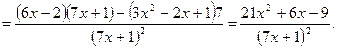
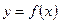 , т.е. такая, что её можно представить в виде:
, т.е. такая, что её можно представить в виде: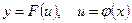
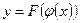 . В выражении
. В выражении 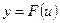 переменная u называется промежуточным аргументом.
переменная u называется промежуточным аргументом.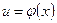 имеет в некоторой точке x производную
имеет в некоторой точке x производную 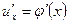 , а функция
, а функция 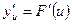 , то сложная функция
, то сложная функция 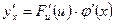 ,
,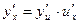 ,
,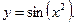 . Найдите
. Найдите 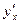 .
.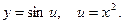
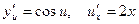 . По правилу дифференцирования сложной функции получаем:
. По правилу дифференцирования сложной функции получаем: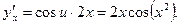
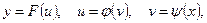 то
то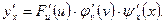
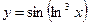 . Найдите
. Найдите 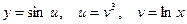 . Тогда
. Тогда 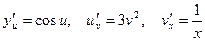 . По рассмотренному выше следствию получаем:
. По рассмотренному выше следствию получаем: