
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Это условие перпендикулярности двух прямых в пространстве.
Пример. Найти угол между прямыми:
Решение: а) Запишем направляющий вектор первой прямой l 1: ` s 1 =(2; –1; 3). Найдем направляющий вектор` s 2 второй прямой. Для этого находим нормальные векторы `N 1 и `N 2 плоскостей, входящих в систему `N 1 = (2; 1; –1) и `N 2 = (2; –1; 3). Затем найдем их векторное произведение:
cosj = = 0. Следовательно, j = 90º (l 1 ^ l 2). б) Запишем направляющие векторы данных прямых:` s 1=(1; 2; –3) и ` s 2 = (–1; –2; 1). Векторы ` s 1 и` s 2 коллинеарны, так как их соответствующие координаты пропорциональны: 1 = 2
= - 1.
Значит прямые l 1 и l 2 параллельны (l 1 || l 2), то есть j = 0º.
Ответ: а) j = 90º, б) j = 0º.
Пример. Доказать перпендикулярность прямых: Решение: Направляющий вектор первой прямой` s 1 =(3; –1; –1). Найдем направляющий вектор ` s 2 второй прямой. Для этого возьмем нормальные векторы `N 1 и `N 2 плоскостей, входящих в систему: `N 1 = (1; –1; 1) и
`N 2 = (1; 1; –1), и вычислим их векторное произведение: Зная` s 1 =(3; 1; –1) и ` s 2 =(0; 2; 2), проверим условие перпендикулярности прямых (1.7.6): 3·0 + 1·2 + (–1)·2 = 0.
Условие выполнено, следовательно, прямые перпендикулярны.
1.7.3. Пусть дана плоскость α: Ax + By + Cz + D = 0 и прямая
Рис.1.7.23 Требуется найти точку пересечения прямой с m n p плоскостью (см. рис. 1.7.23). Перепишем уравнения прямой в параметрическом виде: ì x = x 0 + mt
0
Подставим полученные выражения в уравнение плоскости: A (x 0 + mt) + B (y 0 + nt) + C (z 0 + pt) + D = 0. Возможны три случая: а) Если это уравнение имеет единственное решение t = t 0, то прямая
пересекает плоскость в точке M с координатами: ï y = y + nt 0.
б) Если это уравнение не имеет решений, то прямая параллельна плоскости.
в) Если уравнение имеет бесчисленное множество решений, т.е. имеет вид 0· t = 0, то прямая лежит в плоскости.
Пример. Найти точку пересечения прямой с плоскостью, если: а) l : x - 2 = y = z +1, α1: 2 x – y – 2 z – 8 = 0
1 -1 4 - 3
x - 2 =
y = z +1, α2: x + y + z – 1 = 0
ì x + y - z + 2 = 0, α3: x + 2 y + z – 3 = 0
Решение: а) Запишем уравнения прямой l 1 в параметрическом виде: ì x = 2 - t
Подставим эти уравнения в уравнение плоскости: 2(2 – t) – 4 t – 2(–1 –3 t) – 8 = 0 Þ 4 – 2 t – 4 t +2 + 6 t – 8 = 0 Þ 0· t = 2. Полученное уравнение не имеет решений. Следовательно, прямая l 1 параллельна плоскости α1. б) Рассуждая аналогично, получим:
l 2: í y = -4 t
; (2 + t) + (–4 t) + (–1 + 3 t) – 1 = 0 Þ 0· t = 0 Þ t – любое. Уравнение имеет бесчисленное множество решений. Следовательно, прямая l 2 лежит в плоскости α2. в) l 3: ì x + y - z + 2 = 0.
Запишем уравнение l 3 в параметрическом виде. Для этого найдем точку, лежащую на прямой. Положим z = 0. Тогда l 3: ì x + y + 2 = 0
Þ x = -2; y = 0. Итак M 0(–2; 0; 0). Найдем направляющий вектор ` s. Для этого выпишем нормальные векторы плоскостей: `N 1 = (1; 1; –1) и `N 2 = (1; –1; 0), и вычислим их векторное произведение: ` s = `N 1 ´ `N 2 = (–1; –1; –2). Воспользуемся формулами (1.7.2):
Подставим l 3 в уравнение плоскости α3: x + 2 y + z – 3 = 0. Получим (–2 – t) + 2·(– t) + (–2 t) – 3 = 0 Þ –2 – t – 2 t + –2 t – 3 = 0 Þ –5 t = 5 Þ t = –1. Подставив найденное значение t = –1 в параметрические уравнения прямой l 3, получим точку пересечения прямой l 3 с плоскостью α3.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.109 (0.012 с.) |


 Если прямые l 1 и l 2 параллельны (l 1 || l 2), то их направляющие векторы коллинеарны (` s 1 ||` s 2), то есть
Если прямые l 1 и l 2 параллельны (l 1 || l 2), то их направляющие векторы коллинеарны (` s 1 ||` s 2), то есть
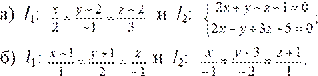
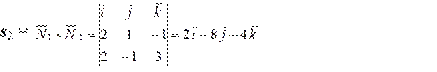
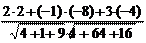 Зная ` s 1 = (2; –1; 3) и ` s 2 = (2; –8; –4), по формуле (1.7.5) получим:
Зная ` s 1 = (2; –1; 3) и ` s 2 = (2; –8; –4), по формуле (1.7.5) получим:
 - 1 - 2
- 1 - 2 1
1
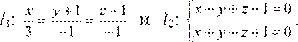
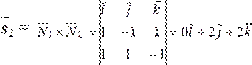

 Взаимное расположение прямой и плоскости. Пересечение прямой с плоскостью
Взаимное расположение прямой и плоскости. Пересечение прямой с плоскостью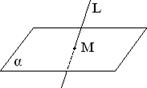


 l: x - x 0 = y - y 0 = z - z 0.
l: x - x 0 = y - y 0 = z - z 0.


 1
1
 - 4 3
- 4 3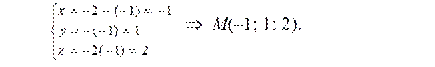
 Ответ: а) l 1 || α1. б) Прямая l 2 лежит в плоскости α2. в) Прямая l 3 пересекает плоскость α3 в точке M (–1; 1; 2).
Ответ: а) l 1 || α1. б) Прямая l 2 лежит в плоскости α2. в) Прямая l 3 пересекает плоскость α3 в точке M (–1; 1; 2).


