
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параллельность прямой и плоскости
Рис.1.7.24 Условие параллельности прямой и плоскости можно получить, используя векторную алгебру. Пусть прямая l параллельна плоскости α (l || α1) (см. рис. 1.7.24). Тогда направляющий вектор ` s прямой l перпендикулярен нормальному вектору ` N плоскости α. Следовательно, скалярное произведение этих векторов равно нулю. Если ` s = (m, n, p), ` N = (A, B, C), то ` s · ` N = 0 или
Пример. Доказать, прямая l: x + 2 = y -1 = z
параллельна плоскости α: 3 x – y + z – 2 = 0. 1 2 -1 Решение: Выпишем направляющий вектор прямой l: ` s = (1; 2; –1) и нормальный вектор плоскости α: ` N = (3; –1; 1). Найдем скалярное произведение этих векторов: ` s · ` N = 1·3 + 2·(–1) + (–1)·1 = 0. Следовательно, прямая l параллельна плоскости α.
Рис.1.7.25 Условие перпендикулярности прямой и плоскости также можно получить, используя векторную алгебру. Пусть прямая l перпендикулярна плоскости α (l ^ α) (см. рис. 1.7.25). Тогда направляющий вектор ` s прямой l будет коллинеарен нормальному вектору ` N плоскости α. Следовательно, соответствующие координаты этих векторов пропорциональны. Пусть ` s = (m, n, p), `N = (A, B, C). Тогда
Пример. Составить уравнение плоскости, проходящей через точку M (1; 2; 3) перпендикулярно прямой x +1 = y -1 = z.
2 -1 3 Решение: Выпишем направляющий вектор прямой: ` s = (2; –1; 3). Вектор ` s можно взять за нормальный вектор ` N искомой плоскости: ` N = ` s. Применяем формулу (1.7.1) 2(x – 1) – 1(y – 2) + 3(z – 3) = 0 Þ 2 x – y + 3 z – 9 = 0
Ответ: 2 x – y + 3 z – 9 = 0.
Пример. Составить уравнение прямой; проходящей через точку M (2; –1; 0) перпендикулярно плоскости x + 2 y – 3 z + 1 = 0. Решение: Выпишем нормальный вектор плоскости: ` N =(1; 2;–3). Вектор ` N можно взять за направляющий вектор искомой прямой: ` s = ` N = (1; 2; – 3). По формулам (1.7.1) запишем канонические уравнения прямой, проходящей через точку M (2; –1; 0): x - 2 = y +1 = z.
1 2 - 3 Ответ: x - 2 = y + 1 = z.
РАЗДЕЛ 2. ВВЕДЕНИЕ В АНАЛИЗ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ И
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ЛЕКЦИЯ 5 Тема 2.1. Функция одной переменной. Предел функции. Бесконечно малые и бесконечно большие функции. Понятие о сходимости числовой последовательности. Функция одной переменной 2.1.1.1. Функция одной переменной. Способы задания функции. 2.1.1.2. Элементы поведения функции. Ограниченные переменные величины и функции. Возрастание и убывание функции на интервале. Чѐтные и нечѐтные функции. Периодические функции. Сложная функция. 2.1.1.3. Основные элементарные функции. Элементарные функции Предел функции. Понятие о сходимости числовой последовательности. 2.1.2.1. Предел переменной величины. 2. 1.2.2. Предел функции при x ® ¥ . 2.1.2.3. Предел функции при точке). x ® x 0 (предел функции в 2.1.2.4. Односторонние пределы функции при x ® x 0.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.74.55 (0.009 с.) |
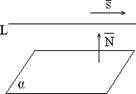
 Полученное условие является условием параллельности прямой и плоскости.
Полученное условие является условием параллельности прямой и плоскости.











 1 2 - 3
1 2 - 3



