
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возрастание и убывание функции на интервале
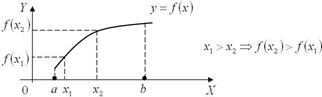
Определение. Функция f (x) называется возрастающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, бóльшему значению аргумента соответствует бóльшее значение функции (рис. 2).
Определение. Функция
f (x) Рис. 2 называется убывающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, бóльшему значению аргумента соответствует меньшее значение функции (рис. 3).
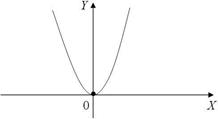
Рис. 3 Интервал, на котором функция возрастает или убывает, называется интервалом монотонности этой функции, а про функцию говорят, что она монотонна на этом интервале. Например y = x 2 (рис. 4). Интервалы монотонности: (- ¥; 0) - функция убывает; (0; + ¥) - функция возрастает (рис.4).
Рис. 4 Чѐтные и нечѐтные функции Определение. Функция y = f (x) называется четной, если ее область определения D симметрична относительно начала координат, и для любого x Î D выполняется условие f (- x) = f (x). Определение. Функция y = f (x) называется нечетной, если ее область определения D симметрична относительно начала координат, и для любого x Î D выполняется условие f (- x) = - f (x). Примеры. 1). f (x) = x 2 D = (- ¥;+ ¥) f (- x) = (- x)2 = x 2 = f (x) Область определения симметрична относительно начала координат и выполняется условие f (- x) = f (x), значит это четная функция. 2). y = 1 x D: x Î(- ¥; 0)U (0; + ¥);
- x = - 1 = - y (x). x
выполняется условие y (- x) = - y (x), значит это нечетная функция. График четной функции симметричен относительно оси ординат, так как наряду с точкой M (x; f (x)) он содержит и симметричную ей относительно оси ординат точку M 1(- x; f (x)) (рис. 5).
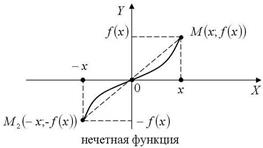
Рис. 5 График нечетной функции симметричен относительно начала координат,
так как наряду с точкой M (x; f (x)) он содержит точку M 2 (- x; - f (x)) (рис. 6). Рис. 6 Не следует думать, что функция, не являющаяся четной, будет нечетной. Чаще всего приходится иметь дело с функциями, которые не являются ни четными, ни нечетными, их обычно называют функциями общего вида. Графики функций общего вида не обладают симметрией ни относительно оси ординат, ни относительно начала координат.
Периодические функции Определение. Число l ¹ 0 называется периодом функции f (x) с областью D, если для любого x Î D f (x + l) = f (x). Это условие предполагает, что наряду с любым x, точка x +lÎ D. Функция f (x), имеющая период, называется периодической. Если l - период функции f (x), то и любое целое число, кратное l (то есть k l, где k = ±1,± 2,...), так же будет периодом f (x). Например,
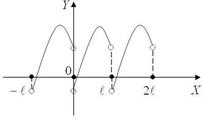
то есть 2l f (x + 2l) = f ((x + l)+ l) = f (x + l) = f (x), тоже является периодом; f (x - l) = f (x - l + l) = f (x), то есть и (- l) тоже является периодом. Наиболее важным является наименьший положительный период, так как все другие периоды будут ему кратны. Поэтому в дальнейшем название периода будем применять к наименьшему положительному периоду. Факт наличия у функции периода достаточно редок. В частности периодическими являются тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x. Для функций p . sin x и cos x - период 2 p, для функций tg x и ctg x - период График периодической функции с периодом l достаточно построить на каком-либо интервале с длиной, равной периоду, а затем построенную часть графика сдвигать вдоль оси Ox на l;- l;2l;- 2l и т.д. (рис. 7).
Рис. 7 Сложная функция Пусть дана функция y = f (u) от аргумента u, причем аргумент u, в свою очередь, является функцией от независимой переменной x: y = f (u), u = u (x). Возьмем какое-либо значение x, ему отвечает определенное значение u = u (x). Полученному значению u, в свою очередь, отвечает определенное значение y = f (u). В конечном итоге взятому значению x соответствует определенное значение y, то есть переменная y оказалась функцией независимой переменной x: y = F (x) или y = f (u (x)) = F (x) Функция F (x) называется сложной функцией от независимой переменной x или функцией от функции (функция f от функции u). Функция y = f (u) называется внешней функцией, а u = u (x) называется внутренней функцией или промежуточной переменной. Отметим, что для того, чтобы образовать функцию от функции нужно, чтобы область значений промежуточной переменной u = u (x) «укладывалась» в область
определения внешней функции y = f (u). Примеры. 1) f (u) = u 2 ; u = cos x, тогда F (x) = f (u (x)) = (cos x)2; 1) f (u) = sin u; u = 3 x -1, тогда F (x) = f (u (x)) = sin(3 x -1). Полезно уметь раскладывать сложную функцию на составляющие, то есть уметь находить внешнюю функцию и промежуточную переменную (или внутреннюю функцию). Примеры. 1) y = 2 x 2; составляющие: u = x 2, f (u) = 2 u; 2)
Функция одной переменной.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.102.112 (0.011 с.) |

 y (- x) = 1
y (- x) = 1 Область определения симметрична относительно начала координат и
Область определения симметрична относительно начала координат и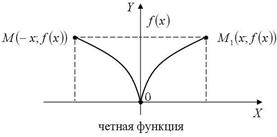
 y = log2 (1 - 5 x); составляющие: u = 1 - 5 x, f (u) = log2 u.
y = log2 (1 - 5 x); составляющие: u = 1 - 5 x, f (u) = log2 u.


