Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
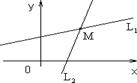
Уравнение прямой, проходящей через две заданные точки
Известно, что через две данные точки можно провести единственную прямую. Рис. 1.6.17 Пусть прямая проходит через точки M 1(x 1, y 1) и M 2(x 2, y 2). За
s = M 1 M 2 = (x 2 - x 1, y 2 - y 1). M 1 M 2.
Получили уравнение прямой по двум точкам. Если x 1 = x 2, то прямая параллельна оси Oy. Ее уравнение имеет вид: x = x 1.
Если y 1 = y 2, то прямая параллельна оси Ox. Ее уравнение: y = y 1.
Пример. Составить уравнение прямой АВ, если А (2, −1); В (1, 3).
Решение: Применяем формулу (1.3.7): Ответ: 4 x + y – 7 = 0.
Пример. Составить уравнение прямой, проходящей через точки М (4, – 2) и N (4, 5).
Решение: Так как x 1 = x 2, то по формуле x = x 1 (см. выше) уравнение прямой имеет вид: x = 4. Прямая параллельна оси Oy.
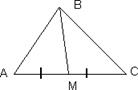
Пример. Дан треугольник АВС, у которого А (1, 2), В (4, 3), С (1, 3). Составить уравнения его сторон. Рис. 1.6.18 Решение. 1)
Найдем уравнение стороны АВ. По формуле(1.3.7)имеем: 2) Сторона ВС находится по формуле y = y 1, так как yB = yC, то y =3. 3) Уравнение стороны АС выпишем по формуле x = x 1, так как xA = xC, то x = 1.
Ответ: AB: x – 3 y + 5 = 0, BC: y = 3; AC: x = 1.
Пример. Даны вершины треугольника АВС А (–1, 3), В (3, –2), С (5, 3). Составить уравнение медианы, проведенной из вершины В. Решение: Пусть ВМ – медиана, тогда точка М является серединой отрезка
АС. По формулам (1.2.2) имеем: Уравнение медианы ВМ получим по формуле
x - 3 =
y - (-2) Þ x - 3 =
y + 2 Þ 4(x - 3) = -(y + 2) Þ 4x + y -14 = 0(1.6.7)
2 - 3 2 - (-2) -1 4
Ответ: BM: 5 x + y – 13 = 0. Уравнение прямой в отрезках
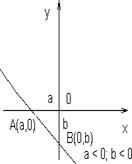
Такое уравнение называется уравнением прямой в отрезках. Рассмотрим это уравнение. Пусть x = 0, тогда y = 1,
y = b. Пусть y = 0, тогда
a x = a. Прямая проходит через точки А (а, 0) и B (0, b) (рис. 1.6.19 – рис.1.6.21).
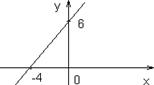
Пример. Записать уравнение прямой 3 x – 2 y + 12 = 0 в отрезках и построить эту прямую.
Решение: 3 x – 2 y = –12. Разделим обе части этого уравнения на –12.
Получим: Следовательно, a = –4, b = 6.
Построим эту прямую. Для этого отложим на оси Ox a = –4, на оси Oy b = 6 и соединим полученные точки. Рис. 1.6.22
Расстояние от точки до прямой Пусть прямая задана уравнением Ax + By + C = 0. Найдем расстояние от точки M 0(x 0, y 0) до этой прямой.
Рис. 1.6.23 Под расстоянием от точки до прямой понимают длину отрезка M 0 M,
Пример. Найти расстояние от точки M 0(2,–1) до прямой, заданной уравнением 3 x + 4 y –22 = 0. Решение: По формуле (1.6.9) получим:
5 5
Ответ: d = 4.
Рис. 1.6.24
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.252.8 (0.01 с.) |
 направляющий вектор ` s данной прямой можно взять вектор
направляющий вектор ` s данной прямой можно взять вектор



 Уравнение прямой по точке M 1(x 1, y 1) и направляющему вектору s имеет вид:
Уравнение прямой по точке M 1(x 1, y 1) и направляющему вектору s имеет вид:
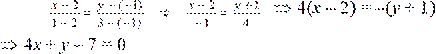


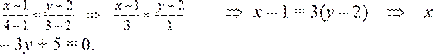
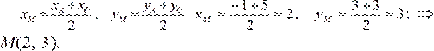



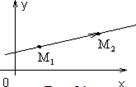
 Если прямая отсекает на осях отрезки а и b, не равные нулю, то ее уравнение имеет вид:
Если прямая отсекает на осях отрезки а и b, не равные нулю, то ее уравнение имеет вид: b
b x = 1,
x = 1,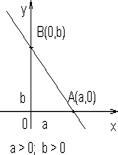


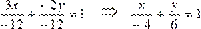
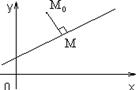
 где М – основание перпендикуляра, опущенного из точки M 0 на данную прямую. Расстояние d = | M 0 M | находим по формуле:
где М – основание перпендикуляра, опущенного из точки M 0 на данную прямую. Расстояние d = | M 0 M | находим по формуле: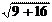

 d = |3 × 2 + 4 × (-1) - 22 | = |6 - 4 - 22 | = 20 = 4.
d = |3 × 2 + 4 × (-1) - 22 | = |6 - 4 - 22 | = 20 = 4. 1.5.2. Взаимное расположение двух прямых, угол между ними.
1.5.2. Взаимное расположение двух прямых, угол между ними.