
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторами, заданными в прямоугольной системе координат
Так как прямоугольные координаты вектора являются его проекциями на координатные оси, то из свойств проекций получаем следующие правила. 1. При сложении двух векторов ā = (x 1, y 1, z 1) и ` b = (x 2, y 2, z 2) их одноименные координаты складываются
2. При умножении вектора ā = (x, y, z) на число каждая координата вектора умножается на это число.
Необходимое и достаточное условие коллинеарности векторов, заданных в координатной форме
пропорциональны:
► Доказательство. Пусть a = (x 1, y 1, z 1), b = (x 2, y 2, z 2).
x = l x, y = l y, z = l z . Найдем l: l = x 1, l = y 1, l = z 1. Получается:
x 1 = y 1 = z 1
1 2 1 2 1 2
.◄. x 2 y 2 z 2 x 2 y 2 z 2 Замечание. Если одна из координат вектора равна нулю, то это означает, что соответствующая координата коллинеарного вектора также равна нулю. Координаты точки в прямоугольной системе координат. Определение координат вектора по известным координатам его начала
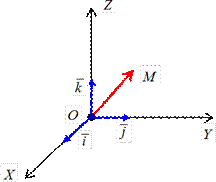
 Определение. Вектор OM, идущий из начала координат в точку M, называется радиусом-вектором точки M (рис.8). Определение. Вектор OM, идущий из начала координат в точку M, называется радиусом-вектором точки M (рис.8).
Рис. 1.5.8 Определение. Прямоугольными координатами точки называются прямоугольные координаты ее радиуса-вектора.
Рис. 1.5.9 Пусть известны координаты точек M 1 = (x 1, y 1, z 1) и M 2 = (x 2, y 2, z 2) (рис.7).
M 1 M 2 Проведем радиусы-векторы этих точек:
OM 1 и OM 2.
OM 1 = (x 1, y 1, z 1), OM 2 = (x 2, y 2, z 2).
OM 1 + M 1 M 2 = OM 2 или M 1 M 2 = OM 2 - OM 1. Окончательно
Правило. Для того, чтобы найти координаты вектора по известным координатам его начала и конца, нужно из координат конца вычесть координаты начала.
1.5.3. Определение скалярного произведения Определение. Углом между векторами называется меньший из углов, образованных этими векторами. На рис.12 угол между векторами обозначен j, причем 0 ≤ j ≤ p.
Рис. 1.5.10 Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.95.244 (0.009 с.) |
||||||||||||||||||||||||||||||||
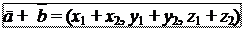




 Для того, чтобы векторы были коллинеарны, необходимо и достаточно, чтобы a = l b, где l – некоторое число (см. лекцию 1), что означает:
Для того, чтобы векторы были коллинеарны, необходимо и достаточно, чтобы a = l b, где l – некоторое число (см. лекцию 1), что означает:

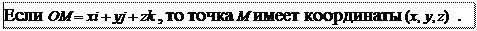



 Найдем координаты вектора
Найдем координаты вектора





 Скалярное произведение двух векторов, определение, свойства, физический смысл скалярного произведения. Вычисление скалярного произведения в прямоугольной системе координат. Направляющие косинусы вектора.
Скалярное произведение двух векторов, определение, свойства, физический смысл скалярного произведения. Вычисление скалярного произведения в прямоугольной системе координат. Направляющие косинусы вектора.


 Обозначается скалярное произведение векторов ā и ` b: (ā,` b) либо a × b.
Обозначается скалярное произведение векторов ā и ` b: (ā,` b) либо a × b.


