Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой по точке и нормальному вектору
Рис. 1.6.15 Пусть прямая проходит через точку M 0(x 0, y 0).
M 0 M = (x - x 0 , y - y 0 ). Вектор n `
скалярное произведение ортогональных векторов равно нулю. Следовательно, уравнение прямой по точке и нормальному вектору имеет вид:
Общее уравнение прямой имеет вид:
Рассмотрим общее уравнение прямой подробнее.
1) Если А = 0, то ` n = (0, B), уравнение примет вид By + C = 0; y = – C.
Прямая параллельна оси Ox. 2) Если В = 0, то
n = (A, 0) , уравнение примет вид: Ax + C = 0, x = – C.
Прямая параллельна оси Oy. 3) B
Прямая
B Из общего уравнения прямой, если В ≠ 0, можно найти угловой коэффициент k. Для этого выразим y из уравнения: Ax + By + C = 0: By = – Ax – C или
B – C.
Пример. Прямая задана уравнением 3 x – 4 y +5 = 0. Найти координаты нормального вектора. Решение: Координатами нормального вектора ` n являются коэффициенты при x и y данного уравнения прямой. Имеем А = 3; В = –4.
 Ответ: ` n = (3, -4). Ответ: ` n = (3, -4).
Решение: Применяем формулу (1.3.3). Имеем 0(x – 2) + 2(y + 1)= 0 Þ 2 y + 2 = 0 Þ y + 1 = 0.
Ответ: y + 1 = 0.
 Решение: Найдем координаты вектора Решение: Найдем координаты вектора 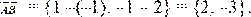 Вектор AB является нормальным вектором искомой прямой. По формуле (1.3.3) имеем Вектор AB является нормальным вектором искомой прямой. По формуле (1.3.3) имеем
Ответ: 2 x – 3 y + 3 = 0.
Уравнение прямой по точке и направляющему вектору:
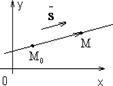
Рис. 1.6.16 Пусть прямая проходит через точку M 0(x 0, y 0).
y) Векторы` s и
M 0 M коллинеарны, следовательно, их соответствующие координаты пропорциональны.
  Полученное уравнение называется уравнением прямой по точке и направляющему вектору. Полученное уравнение называется уравнением прямой по точке и направляющему вектору.
Пример. Прямая задана уравнением x + 2 = y - 3.
Написать координаты -1 2 направляющего вектора; найти координаты точки, лежащей на прямой; составить общее уравнение прямой.
приравняв нулю числители данного уравнения: x + 2 = 0 Þ x = -2, y - 3 = 0,Þ y = 3. Итак, M 0(−2; 3). Общее уравнение прямой получим по свойству пропорций: (x + 2 ) 2 = (y - 3 )( -1 ) Þ 2 x + 4 = - y + 3 Þ 2 x + y +1 = 0
 Ответ: ` s = (-1, 2), M 0 (−2; 3), 2 x + y + 1 = 0. Ответ: ` s = (-1, 2), M 0 (−2; 3), 2 x + y + 1 = 0.
Пример. Составить уравнение прямой по точке М (2, −5) и направляющему
Решение: Применяем формулу (1.6.6). Имеем:
-2 4 Þ 4(x - 2) = -2(y + 5) Þ 4x + 2y + 2 = 0 Þ 2x + y +1 = 0
Ответ: 2 x + y + 1 = 0.
, где А (2, −1), В (3, 4).
Применяем формулу (1.6.6). Имеем:
Ответ: 5 x – y + 11 = 0.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.166.61 (0.013 с.) |
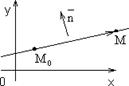
 Под нормальным вектором понимают ненулевой вектор, который перпендикулярен данной прямой. Обозначим его` n = (A, B).
Под нормальным вектором понимают ненулевой вектор, который перпендикулярен данной прямой. Обозначим его` n = (A, B).
 Возьмем на прямой произвольную точку M (x, y) и рассмотрим вектор
Возьмем на прямой произвольную точку M (x, y) и рассмотрим вектор M 0 M. Его координаты равны
M 0 M. Его координаты равны перпендикулярен вектору M 0 M. Из векторной алгебры известно, что
перпендикулярен вектору M 0 M. Из векторной алгебры известно, что Коэффициенты А и В в уравнении определяют координаты нормального вектора: ` n = (A, B).
Коэффициенты А и В в уравнении определяют координаты нормального вектора: ` n = (A, B). B
B A
A Если С = 0, то уравнение примет вид: Ax + By = 0, y = – A x.
Если С = 0, то уравнение примет вид: Ax + By = 0, y = – A x. проходит через начало координат и имеет угловой коэффициент k = – A.
проходит через начало координат и имеет угловой коэффициент k = – A. Угловой коэффициент прямой на плоскости:
Угловой коэффициент прямой на плоскости:
 Пример. Составить уравнение прямой, проходящей через точку М (0; 1) перпендикулярно вектору AB, где А (–1; 2), В (1; –1).
Пример. Составить уравнение прямой, проходящей через точку М (0; 1) перпендикулярно вектору AB, где А (–1; 2), В (1; –1).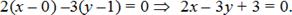

 Определение. Направляющим вектором ` s данной прямой называется ненулевой вектор, параллельный этой прямой.
Определение. Направляющим вектором ` s данной прямой называется ненулевой вектор, параллельный этой прямой. Пусть дан вектор s = (m, n). Возьмем на прямой произвольную точку M (x,
Пусть дан вектор s = (m, n). Возьмем на прямой произвольную точку M (x, и рассмотрим вектор
и рассмотрим вектор


 Решение: Направляющий вектор s = (-1, 2). Точку M 0 мы получим,
Решение: Направляющий вектор s = (-1, 2). Точку M 0 мы получим,
 вектору s = (-2, 4).
вектору s = (-2, 4).
 x - 2 = y - (-5)
x - 2 = y - (-5) Пример. Через точку С (−2, 1) провести прямую, параллельную вектору AB
Пример. Через точку С (−2, 1) провести прямую, параллельную вектору AB Решение: Вектор AB можно взять за направляющий вектор данной прямой.
Решение: Вектор AB можно взять за направляющий вектор данной прямой.