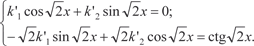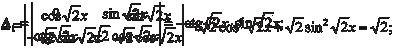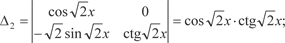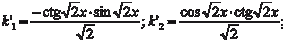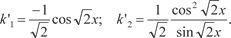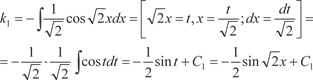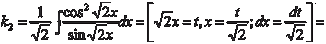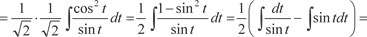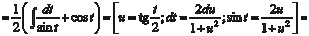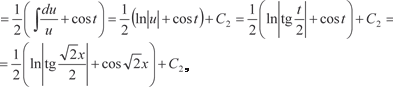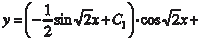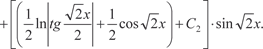Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий вид таких дифференциальных уравнений следу- ющий: y ″ + ay ′ + by = f (x). (6.44) Общее решение такого дифференциального уравнения по- лучается суммированием общего решения соответствующего однородного дифференциального уравнения с постоянными коэффициентами y ″ + ay ′ + by = 0 и какого-то частного решения дифференциального уравнения (6.44). Так как нахождение общего решения дифференциаль- ного уравнения вида (6.38) мы рассмотрели раньше, то ос- тается найти любое частное решение дифференциального уравнения (6.44). Рассмотрим некоторые частные случаи, в которых реше- ние можно найти методом неопределенных коэффициентов. 1. Предположим, что правая часть дифференциального уравнения (6.44) имеет вид
где P 1(x) — многочлен. Тогда дифференциальное уравнение (6.44) имеет частное решение вида у = хmP (x) enx, где P (x) — многочлен той же сте- 2 2 пени, что и P 1(x), причем если число n не является корнем ха- рактеристического уравнения k 2 + ak + b = 0, то m = 0, а если является, то m — кратность этого корня. Взяв решение в указанной форме, находим неизвестные коэффициенты многочлена P 2(x) по способу неопределенных коэффициентов. Правило сохраняется и в том случае, когда n = = 0, т. е. в правой части стоит только многочлен P 1(x) (в этом случае надо проверить, не является ли ноль корнем характе- ристического уравнения, в частном случае многочлен P 1(x) мо- жет быть нулевой степени, т. е. постоянной величиной). Рассмотрим конкретный пример. Пример 6.23. Найдем общее решение дифференциального уравнения: y ″ + 3 y ′ − 4 y = 4 + x. Сначала найдем общее решение соответствующего одно- родного уравнения y ″ + 3 y ′ − 4 y = 0. Его характеристическое уравнение имеет вид: k 2 + 3 k − 4 = 0 D = 9 − 4⋅1(−4) = 25
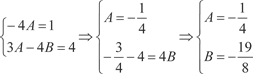
Значит общее решение однородного дифференциального уравнения будет равно y = C ex + C e −4 x. 1 1 2 Правая часть рассматриваемого дифференциального урав- нения имеет вид P (x) enx, причем n = 0, а P (x) = 4 + х. 1 1 Так как ноль не является корнем характеристического уравнения k 2 + 3 k − 4 = 0, то частное решение заданного диффе- ренциального уравнения ищем в виде y 2 = Ax + B, где А и В — постоянные, которые нужно найти. Находим y ′2 = A; y ″2 = 0 и подставляем в исходное дифференциальное уравнение. Тогда получаем:
Поэтому частным решением заданного дифференциально- го уравнения будет функция А его общим решением — функция
2.
f (x) = a cos nx + b sin nx. (6.46) Если числа ± in не являются корнями характеристического уравнения, то дифференциальное уравнение (6.44) имеет част- ное решение вида y = A cos nx + B sin nx. Если числа ± in есть корни характеристического уравне- ния, то частное решение (6.44) имеет вид y = х (A cos nx + B sin nx). В тех случаях, когда или а =0, или b =0 решение нужно ис- кать в указанном виде. Пример 6.24. В качестве примера найдем общее решение дифференциального уравнения y ″ + 4 y ′ + 13 y = 3cos 2 x. Сначала находим общее решение соответствующего одно- родного дифференциального уравнения y ″ + 4 y ′ + 13 y = 0. Его характеристическое уравнение имеет вид: (k 2 + 4 k + 13) = 0; D = −36; k 1 = −2 + 3 i; k 2 = −2 − 3 i. А его общее решение таково y 1 = e −2 x (C 1cos 3 x + C 2sin 3 x). Теперь находим частное решение исходного дифференци- ального уравнения. Его правая часть имеет вид (6.46), причем a = 3; b = 0; n = 2. Числа ±2 i не являются корнями характерис- тического уравнения, поэтому частное решение заданного не- однородного дифференциального уравнения ищем в виде y 2 = = A cos 2x + B sin 2x, где А и В — неизвестные коэффициенты, которые надо найти. Дважды дифференцируем у 2 и результаты подставляем в исходное дифференциальное уравнение. Тогда получаем: y ′2 = −2 A sin 2 x + 2 B cos 2 x; y ″2 = −4 A cos 2 x − 4 B sin 2 x; −4 A cos 2 x − 4 B sin 2 x + 4(−2 A sin 2 x + 2 B cos 2 x) + + 13 A cos 2 x + 13 B sin 2 x = 3cos 2 x; −4 A cos 2 x − 4 B sin 2 x − 8 A sin 2 x + 8 B cos 2 x + + 13 A cos 2 x + 13 B sin 2 x = 3cos 2 x.
Теперь приравниваем друг к другу одноименные коэффи- циенты при sin2 x и cos2 x и получаем:
И частное решение исходного дифференциального урав- нения будет следующим: Поэтому общее решение заданного дифференциального уравнения будет следующим:
3. Пусть правая часть дифференциального уравнения (6.44) имеет вид f (x) = emx [ P 1(x)cos nx + P2(x)sin nx ], (6.47) где P 1(x) и P 2(x) многочлены. Если числа m±in не являются корнями характеристическо- го уравнения, то частное решение уравнения (6.44) ищут в виде y = emx [ R 1(x)cos nx + R 2(x)sin nx ]. Если же числа m ± in являются корнями характеристическо- го уравнения, то частное решение уравнения (6.44) ищут в виде y = xemx [ R 1(x)cos nx + R 2(x)sin nx ], где R 1(x) и R 2(x) — многочлены степени, равной высшей из сте- пеней многочленов P 1(x) и P 2(x). Пример 6.25. Найти общее решение дифференциального уравнения y ″ + + y = 4 x sin x; m = 0; P 1(x) = 0; P 2(x) = 4 x; n = 1. Этот пример дается в качестве самостоятельного задания. Можно убедиться, что общее решение данного урав- нения имеет вид y = С1cos x + C2sin x + x (- x cos x + sin x) Теперь приведем метод Лагранжа (способ вариации про- извольных постоянных), который позволяет находить общее решение дифференциального уравнения y ″ + ay ′ + by = f (x), где f (x) — любая функция. Чтобы применить описываемый метод, надо знать общее решение соответствующего однородного дифференциального уравнения y ″ + ay ′ + by = 0, (6.48) где а и b могут быть как числами, так и некоторыми функциями от х. Будем считать, что а и b — числа. Предположим, что дифференциальное уравнение (6.48), соответствующее дифференциальному уравнению (6.44), име- ет общее решение: y = C 1 y 1 + C 2 y 2, где С 1 и С 2 — произвольные постоянные. Будем искать общее решение дифференциального уравне- ния (6.44) в виде y = k 1(x) y 1 + k 2(x) y 2. (6.49) Здесь k 1(x) и k 2(x) — неизвестные функции, которые надо определить, а у 1 и у 2 — известные частные решения дифферен- циального уравнения (6.48). Продифференцируем (6.49) и получим: y ′ = k ′1(x) y 1 + k 1(x) y ′1 + k ′2(x) y 2 + k 2(x) y ′2. Так как надо найти две функции k 1(x) и k 2(x), то одним из соотношений между ними можно распорядиться произвольно. Поэтому положим k ′1(x) y 1 + k ′2(x) y 2 = 0. (6.50) Тогда y ′ = k 1(x) y ′1 + k 2(x) y ′2. Последнее выражение продифференцируем второй раз и получим: y ″ = k ′1(x) y ′1 + k 1(x) y ″1 + k ′2(x) y ′2 + k 2(x) y ″2. Теперь подставим в левую часть дифференциального уравнения (6.44) y, y ′, y ″ и получим: k ′1(x) y ′1 + k 1(x) y ″1 + k ′2(x) y ′2 + k 2(x) y ″2 + ak 1(x) y ′1 + ak 2(x) y ′2 + + bk 1(x) y 1 + bk 2(x) y 2 = k ′1(x) y ′1 + k ′2(x) y ′2 + k 1(x)(y ″1 + + ay ′1 + by 1) + k 2(x)(y ″2 + ay ′2 + by 2) = f (x); y ″1 + ay ′1 + by 1 = 0; y ″2 + ay ′2 + by 2 = 0, так как у 1 и у 2 есть частные решения дифференциального урав- нения (6.48). Поэтому для того, чтобы функция (6.49) была общим реше- нием (6.44) необходимо выполнения двух условий.
Для того чтобы система (6.51) имела решения, необходимо, чтобы ее определитель не был равен нулю, т. е. Заметим, что этот определитель называется определите- лем Вронского. Из системы (6.51) сначала находим k ′1(x) и k ′2(x), а затем интегрированием определяем сами функции k 1(x) и k 2(x). Если при интегрировании k ′1(x) и k ′2(x) ввести произвольные посто- янные, то сразу получим общее решение дифференциального уравнения (6.44). Рассмотрим конкретный пример.
Исходному дифференциальному уравнению соответству- ет однородное дифференциальное уравнение y ″ + 2 y = 0, харак- теристическое уравнение которого имеет вид
Поэтому запишем общее решение исходного дифференци- ального уравнения в виде
А затем составим систему уравнений (6.51) для нахожде- ния k ′1 и k ′2
Решаем систему и получаем
Интегрируем k ′1, k ′2 и находим
где С 1 — произвольная постоянная.
где С 2 — произвольная постоянная.
Теперь общее решение исходного дифференциального уравнения мы запишем в виде:
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.173.112 (0.031 с.) |
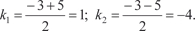
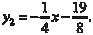
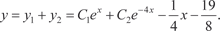
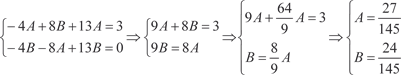
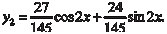
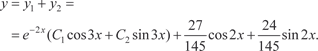
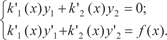 (6.51)
(6.51)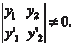
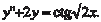
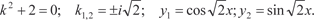
 , здесь k 1 и k 2 — функции от x.
, здесь k 1 и k 2 — функции от x.