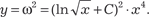Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
К линейным дифференциальным уравнениям относятся дифференциальные уравнения вида: y ′ + p (x) y = q (x), (6.11) т. е. линейное относительно неизвестной функции и ее произ- водной. В уравнении (6.11) p (x) и q (х) — известные функции ар- гумента х. Рассмотрим метод Бернулли. По этому методу дифферен- циальное уравнение (6.11) сводится к двум дифференциаль- ным уравнениям с разделяющимися переменными с помощью следующего приема. Представим функцию у в виде произведения двух функ- ций y = uv. Одной из этих функций можно распорядиться про- извольно, а вторая при этом должна быть определена в зави- симости от первой так, чтобы их произведение удовлетворяло исходному дифференциальному уравнению. Свободой выбора одной из функций u и v надо воспользоваться для упрощения дифференциального уравнения, получающегося после замены. Из равенства y = uv получим y ′ = u ′ v + v ′ u. Это выражение подставим в (6.11) и получим: u ′ v + v ′ u + p (x) uv = q (х); u ′ v + u (v ′ + p (x) v) = q (х). В качестве v выберем какое-нибудь частное решение диф- ференциального уравнения v ′ + p (x) v = 0. (6.12) Тогда для нахождения u получим дифференциальное уравнение u ′ v = q (х) . (6.13)
Из дифференциального уравнения (6.12) находим v.
Под неопределенным интегралом в выражении (6.14) по- нимается какая-то одна первообразная от функции p (x), т. е. v есть вполне определенная функция от х.
Теперь, используя найденное значение функции v из урав- нения (6.13), находим функцию u.
Интегрируем обе части последнего выражения и получаем
В формуле (6.15) для функции u берутся все первообразные. Зная функции u и v, находим искомую функцию у.
Выражение (6.16) является общим решением линейного дифференциального уравнения первого порядка. Пример 6.8. Найдем общее решение линейного дифферен- циального уравнения
Используем подстановку y = uv ⇒ y ′ = u ′ v + v ′ u и получим В качестве v выберем какое-то частное решение диффе- ренциального уравнения
Находим функцию v
Зная v, находим функцию u Зная функции u и v, находим исходную функцию у y = uv = x 3(x + C). (6.17) Выражение (6.17) есть общее решение исходного диффе- ренциального уравнения.
Линейные дифференциальные уравнения первого порядка с постоянными коэффициентами Общий вид таких дифференциальных уравнений следую- щий: y ′ + ay = b, (6.18) где a, b ∈ R [35], т. е. это частный случай уравнения (6.11).
Дифференциальное уравнение вида (6.18) решается раз- делением переменных, т. е. Интегрируем левую и правую части последнего выраже- ния и получаем:
Так как постоянная может быть любая, обозначим
Пример 6.9. Найдем общее решение дифференциального уравнения
y ′ + 2 y + 5 = 0.
Теперь рассмотрим метод Лагранжа решения уравне- ния (6.11). В соответствии с этим способом сначала рассмотрим дифференциальное уравнение (6.11), но без правой части, оно называется линейным однородным дифференциальным урав- нением. y ′ + p (x) · y = 0. (6.20)
Перепишем последнее дифференциальное уравнение сле- дующим образом: Получили дифференциальное уравнение с разделяющи- мися переменными. Разделяя эти переменные, получаем:
Интегрируя обе части последнего выражения, имеем:
Постоянная может быть любой, поэтому обозначим ± С 1 = С и тогда получим:
Метод Лагранжа состоит в том, что постоянную С в полу- ченном решении (6.21) заменяем функцией от х, т. е. полагаем, что С = С (х). А решение исходного дифференциального урав- нения (6.11) ищем в виде
Дифференцируем формулу (6.22) по х и получаем: Подставляем у и у ’ в исходное дифференциальное уравне- ние (6.11).
Последнее дифференциальное уравнение — уравнение с разделяющимися переменными. Разделяя эти переменные, на- ходим: Интегрируя обе части последнего выражения, определяем неизвестную функцию С (х).
где С0 — постоянная.
Подставляем найденное значение С (х) в формулу (6.22) и получаем общее решение дифференциального уравнения (6.11). Это решение, естественно, совпадает с тем, которое мы по- лучили по методу Бернулли. Пример 6.10.
Найти общее решение или общий интеграл следующего дифференциального уравнения: Используем метод Лагранжа и рассмотрим однородное ли- нейное дифференциальное уравнение.
Данное дифференциальное уравнение — уравнение с раз- деляющимися переменными. Разделяя переменные, получаем Интегрируя обе части последнего выражения, получаем: ln | y | = -ln | x | + ln | C 1|;
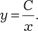
Будем искать решение исходного дифференциального уравнения в виде Дифференцируем это выражение и находим:
Подставляя у и у ’ в исходное дифференциальное уравне- ние, получаем:
Следовательно, общее решение исходного дифференци- ального уравнения будет иметь вид Естественно это решение можно получить и методом Бер- нулли.
Уравнение Бернулли Дифференциальное уравнение вида y ′ + p (x) y = q (x) yn, где n ∈ R, называется уравнением Бернулли. Заметим, что его оче- видное решение у = 0. При n = 0 данное уравнение будет ли- нейным, при n = 1 — с разделяющимися переменными, а при любых других n оно сводится к линейному с помощью подста- новки ω = у 1 – n.
.
. Тогда получаем:
Последнее дифференциальное уравнение является линей- ным; решение таких уравнений мы рассматривали. Находим общий интеграл полученного линейного уравнения и, подстав- ляя вместо ω выражение у 1 – n, находим общее решение уравне- ния Бернулли. Пример 6.11. Найдем общее решение дифференциального уравнения Данное уравнение является уравнением Бернулли с n = 1/2. Поэтому используем подстановку
Тогда получим . Теперь осуществляем под- становку
 , или , или
, т. е. получили линейное уравнение, из решения которого и найдем неизвестную функцию ω.
Применим подстановку ω = U · V, тогда ω' = U ’· V + U · V ’ и линейное уравнение примет вид
из дифференциального уравнения . Определяем функцию V:
Зная U и V, вычисляем ω:
Теперь находим искомую функцию:
Это и есть общее решение исходного уравнения Бернулли. Его решением является и ноль, т. е. у = 0. Заметим, что урав- нение Бернулли можно решить сразу, применив подстановку y = U · V.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.203 (0.031 с.) |
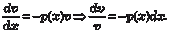



 .
. (6.15)
(6.15) (6.16)
(6.16) .
.
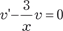 , тогда u можно найти из дифференциального уравнения u ′ v = x 3.
, тогда u можно найти из дифференциального уравнения u ′ v = x 3.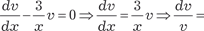
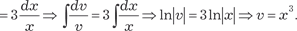
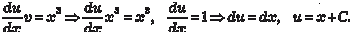

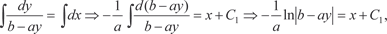
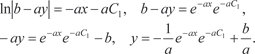
 и получаем общее решение дифференциального уравнения (6.18)
и получаем общее решение дифференциального уравнения (6.18)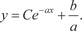

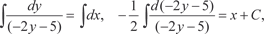
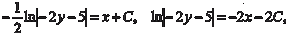

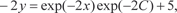
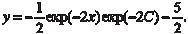

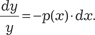
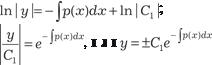 .
. (6.21)
(6.21) . (6.22)
. (6.22)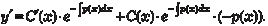
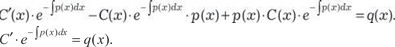

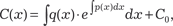
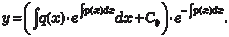
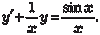
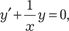 или
или 
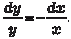

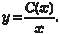

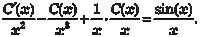
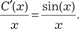

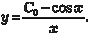

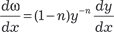
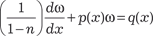

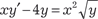 .
. . Делим все элементы
. Делим все элементы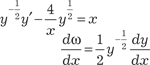 исходного уравнения на
исходного уравнения на 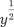 и получаем
и получаем 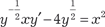 . Разде- лим обе части этого уравнения на х ≠ 0.
. Разде- лим обе части этого уравнения на х ≠ 0. , замечая, что .
, замечая, что .
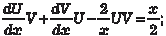
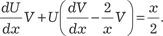
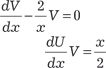 В качестве V выберем какое-либо частное решение диф- ференциального уравнения , тогда U можно найти
В качестве V выберем какое-либо частное решение диф- ференциального уравнения , тогда U можно найти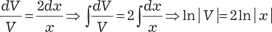 , или V = x 2. Зная V, находим функцию U:
, или V = x 2. Зная V, находим функцию U: