
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения в полных дифференциалах. Интегрирующий множитель
Сначала поясним понятие полного дифференциала функ- ции двух независимых аргументов.
Полный дифференциал функции двух независимых аргу- ментов W (x, y) равен сумме произведений частных производ- ных на дифференциалы соответствующих независимых пере- менных, т. е. Дифференциальное уравнение первого порядка P (x, y) dx +
+ Q (x, y) dy = 0 называется уравнением в полных дифференци- алах, если его левая часть есть полный дифференциал некото- рой функции W(x,y), т.е. должно выполняться условие: Поэтому исходное уравнение можно переписать в виде dW = 0, т. е. решение уравнения в полных дифференциалах имеет вид W (x, y) = С, где С = const. Следовательно, для на- хождения решения уравнения в полных дифференциалах надо проинтегрировать его левую часть, т. е. найти интеграл от пол- ного дифференциала. Приведем окончательные формулы, не касаясь их вывода, который выходит за рамки этой книги, вы- вод можно найти, например, в [9].
Итак, общее решение исходного уравнения можно запи- сать в виде или
Точку (х 0, у 0) обычно выбирают так, чтобы подынтеграль- ные функции были более простыми. Можно получить общее
 и и 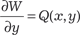 , получим , получим
, где С (у) — произвольная функция от у. Дифференцируем найденную функцию W (x, y) по у и по- лучаем Пример 6.12. Найдем общее решение дифференциального уравнения (x 2 + 2 xy + 4) dx + (x 2 + y 2 – 4) dy = 0.
;
В соответствии с приведенными формулами будем искать общее решение данного уравнения, приняв в качестве точки (х 0, у 0) начало координат (х 0 = 0, у 0 = 0): или
Последнее выражение и есть общее решение исходного дифференциального уравнения. Если левая часть дифференциального уравнения P (x, y) dx + + Q (x, y) dy = 0 не является полным дифференциалом, то иногда удается подобрать такую функцию λ(х, у), после умножения на которую всех элементов уравнения его левая часть становится полным дифференциалом. Общее решение полученного таким образом уравнения совпадает с общим решением первоначаль- ного уравнения, а функция λ(х, у) носит название интегрирую- щего множителя заданного уравнения.
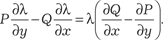
Для определения λ(х, у) умножаем на него обе части исход- ного уравнения и получаем λ Pdx + λ Qdy = 0. Чтобы это уравнение было уравнением в полных диффе- ренциалах необходимо и достаточно выполнение условий:
или
Таким образом, что для того чтобы найти λ(х, у), надо про- интегрировать дифференциальное уравнение в частных про- изводных, а это очень непростая задача. Ее можно упростить, если предположить, что λ-функция только одного аргумента (или х, или у). Например, пусть λ = λ(х), тогда имеем
Заметим, что в этом выражении подынтегральная функ- ция зависит от х.
, здесь подынтегральная функция за- висит только от у. Пример 6.13. Найти общее решение дифференциального уравнения (2 y + xy 3) dx + (x + x 2 y 2) dy = 0.
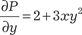 ; ;
, т. е условие не выполняется. Попробуем
найти интегрирующий множитель λ. Будем считать, что он за- висит только от аргумента х, т. е. λ = λ(х). Тогда получаем: ln|λ| = ln | x | или λ = х. Умножаем обе части исходного уравнения на найденный интегрирующий множитель и получаем (2 xy + x 2 y 3) dx + (x 2 + + x 3 y 2) dy = 0. Находим Примем в качестве точки (х 0, у 0) начало координат, т. е. х 0 = 0; у 0 = 0. Тогда получим
или
Это и есть общее решение заданного дифференциального уравнения.
Уравнения Лагранжа и Клеро Эти дифференциальные уравнения являются неразре- шенными относительно производной. Уравнение Лагранжа имеет вид y = x · ϕ(y ′) + ψ(y ′), (6.23) где ϕ(y ′) и ψ(y ′) — известные функции, зависящие от у ′. Делаем замену, обозначим y ′ = p, тогда уравнение (6.23) примет вид y = x · ϕ(p) + ψ(p). (6.24)
или Продифференцируем уравнение (6.24) по х и получим
Из данного дифференциального уравнения можно сра- зу найти некоторые решения, а именно оно будет обращаться в тождество при любом постоянном значении р = р 0, которое удовлетворяет условию р 0 − ϕ(р 0) = 0. Видно, что при постоянном значении р производная y = x · ϕ(p 0) + ψ(p 0). Если данное значение не следует из общего решения ни при каком значении произвольной постоянной, то оно является особым решением. Теперь найдем общее решение уравнения Лагранжа. Для этого уравнение (6.25) преобразуем к следую- щему виду:
Последнее дифференциальное уравнение будет линейным относительно функции х и ее производной по аргументу р. Ре- шая его, определяем х = λ(р, С). (6.26) Далее исключаем параметр р из уравнений (6.24) и (6.26) и находим общее решение уравнения Лагранжа: y = μ(x, С). (6.27) Уравнение Клеро является частным случаем уравнения Лагранжа и имеет вид y = x · y ’ + ψ(y ’). (6.28) Обозначим y ’ = p и тогда уравнение (6.28) примет вид y = x · p + ψ(p). (6.29)
Дифференцируем это уравнение по х и получаем: или
Из последнего выражения следует, что, если y = x · С + ψ(С). (6.30) Если х + ψ′(р) = 0, то получаем частное решение исходного уравнения в параметрической форме:
Решение (6.31) называется особым решением уравнения Клеро и не содержится в общем решении (6.30). Если параметр р удается исключить, то можно получить особое решение в виде η(х, у) = 0. Теперь приведем конкретные примеры. Пример 6.14. Решить уравнение Лагранжа.
Полагаем y ’ = p и тогда получаем: Дифференцируем последнее выражение по х:
Разделяем переменные и получаем:
Теперь интегрируем обе части последнего уравнения: Следовательно, общее решение исходного уравнения бу- дет иметь вид
Исключим параметр p: Проверяем, есть ли у исходного уравнения особое решение. В то случае, если Следовательно, Это и есть особое решение исходного уравнения Лагранжа.
Решить уравнение Клеро .
Делаем замену y ’ = p и тогда получаем . Последнее равенство дифференцируем по х .
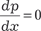 получаем p = С и имеем следую- щее общее решение исходного уравнения получаем p = С и имеем следую- щее общее решение исходного уравнения  . .
(6.32)
Исключим параметр p. Из первого уравнения системы (6.32) имеем Из второго уравнения системы (6.32) получаем Следовательно, можно записать Учитывая, что p = у ′, получаем следующее дифференци- альное уравнение:
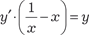 , или , т. е. по- лучили дифференциальное уравнение с разделяющимися пе- ременными. Разделяя переменные, получаем , или , т. е. по- лучили дифференциальное уравнение с разделяющимися пе- ременными. Разделяя переменные, получаем 
, или
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.27.202 (0.051 с.) |
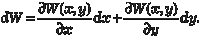
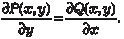
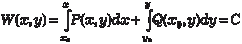
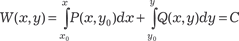
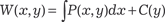
 . Из последнего уравнения находим С ’(у) и, интегрируя, получаем С (у).
. Из последнего уравнения находим С ’(у) и, интегрируя, получаем С (у).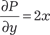
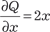 ,
,  , т. е. данное уравнение является урав- нением в полных дифференциалах.
, т. е. данное уравнение является урав- нением в полных дифференциалах.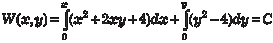


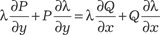
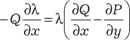 или
или 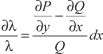 . Окончательно получаем:
. Окончательно получаем: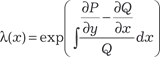 .
.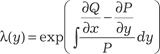

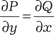
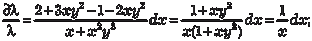
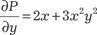 ;
; 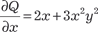 , т. е.
, т. е. 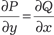 . Итак, мы получили дифференциальное уравнение в полных дифференциалах.
. Итак, мы получили дифференциальное уравнение в полных дифференциалах.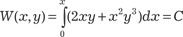 ,
,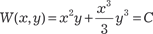
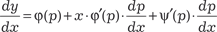 ,
,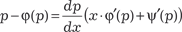
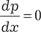 и обе части уравнения (6.25) обращаются в ноль. Решение, ко- торое соответствует любому р = р 0, будет линейной функцией от х. Чтобы найти эту функцию надо подставить в (6.24) значе- ние р = р 0, т. е.
и обе части уравнения (6.25) обращаются в ноль. Решение, ко- торое соответствует любому р = р 0, будет линейной функцией от х. Чтобы найти эту функцию надо подставить в (6.24) значе- ние р = р 0, т. е.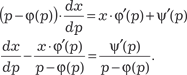 ;
;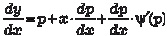

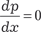 , то р = С, где С — постоянная. С учетом (6.29) получаем общее ре- шение уравнения Клеро:
, то р = С, где С — постоянная. С учетом (6.29) получаем общее ре- шение уравнения Клеро: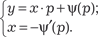 (6.31)
(6.31)
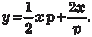
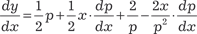
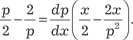
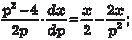
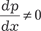
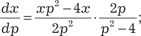
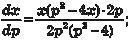
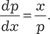
 .
.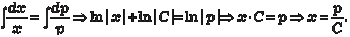
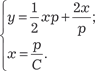
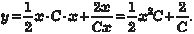
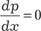 , p 2 – 4 = 0. Отсюда имеем p 2 = 4 → p = ±2.
, p 2 – 4 = 0. Отсюда имеем p 2 = 4 → p = ±2.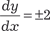 , a y = ±2 x.
, a y = ±2 x.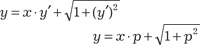 Пример 6.15.
Пример 6.15.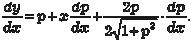
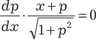
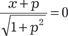
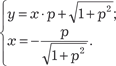
 .
.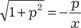 .
. .
. , или
, или 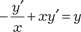 .
.
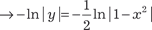
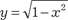 , т.е. y 2 + x 2 = 1.
, т.е. y 2 + x 2 = 1.


