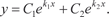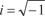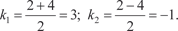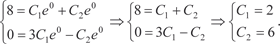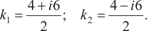Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

К ним относятся дифференциальные уравнения вида

y ″ + ay ′ + by = 0,                           (6.38)

где a ∈ R, b ∈ R.

Приведем без доказательства теоремы, помогающие на- ходить общее решение дифференциального уравнения вида (6.38).

Теорема 6.3. Если функция y = y 1 — это решение диффе- ренциального уравнения (6.38), то и функция y = Сy 1 (С = const) также решение дифференциального уравнения (6.38).

Теорема 6.4. Если функции y = y 1 и y = y 2 есть решения дифференциального уравнения (6.38), то и функция y = y 1 + у 2 также решение дифференциального уравнения (6.38).

При этом у 1 и у 2 называются частными решениями (6.38).

Два частных решения дифференциального уравнения (6.38) называют линейно независимыми, если одно из них не может быть представлено как другое, умноженное на некото- рый постоянный коэффициент С, т. е. y 2 ≠ Сy 1.

Теорема 6.5. Если у 1 и у 2 — линейно независимые частные

решения уравнения (6.38), то его общее решение имеет вид

y = С 1 y 1 + С 2 у 2,                               (6.39)

где С 1 и С 2 — постоянные.

Для того чтобы найти общее решение уравнения (6.38), имеющее вид (6.39), надо найти два линейно независимых час- тных решения у 1 и у 2.

Л. Эйлер предложил искать частное решение уравнения

(6.38) вида y = e^kx, где k = const и k необходимо подобрать [9, 44, 59].

Чтобы найти значение k, при котором y = e^kx будет решени- ем дифференциального уравнения (6.38), подставим y = e^kx и ее производные первого и второго порядка в это дифференциаль- ное уравнение. Получим

y ′ = ke^kx; y ″ = k ² e^kx,

 

значит

k ² e^kx + ake^kx + be^kx = 0.

e^kx (k ² + ak + b) = 0,

e^kx ≠ 0 для ∀ x,

 

k ² + ak + b = 0.                               (6.40)

Уравнение (6.40) называется характеристическим урав- нением для дифференциального уравнения (6.38). Решая его, можно найти неизвестные постоянные k 1 и k 2.

При решении уравнения (6.40) возможны три случая:

1. D > 0, k 1 ≠ k 2, общее решение уравнения (6.38) имеет вид:

(6.41)

 

2. D = 0, k 1 = k 2 = k. В этом случае y 1 = e и можно доказать,

kx

что y 2 = xe, а общее решение уравнения (6.38) имеет вид:

kx

 

(6.42)

3. D < 0, k 1 и k 2 — комплексно-сопряженные корни вида

k 1 = c + ip; k 2 = c − ip,

где      .

Частные решения дифференциального уравнения (6.38) в этом случае имеют вид:

1                           2

y = e (c + ip) x; y = e (c − ip) x.

Как правило, чтобы не иметь мнимых величин в показа- теле степени, эти решения преобразуют, используя формулы Л. Эйлера.

e^ix = cos x + i sin x; e ^{− ix} = cos x − i sin x.

Для рассматриваемого случая получаем:

1

y = e ^{( c + ip ) x} = e^cxe^ipx = e^cx (cos px + i sin px);

2

y   = e ^{( c - ip ) x} = e ^cx e ^{− ipx} = e ^cx (cos px − i sin px).

Поэтому общее решение дифференциального уравнения (6.38) имеет вид:

y = C e^cx (cos px + i sin px) + C e^cx (cos px − i sin px) =

I                                              II

= C e^cx cos px + iC e^cx sin px + C e^cx cos px − iC e^cx sin px =

I                         I                       II                          II

I   II                           I   II

= e^cx cos px (C + C) + ie^cx sin px (C − C). Введем следующие обозначения:

С 1 = С I + С II и C 2 = i (C I − C II)

и окончательно получим:

1                            2

y = e^cx (C cos px + C sin px).                     (6.43) Теперь рассмотрим конкретные примеры.

Пример 6.20.

Найдем частное решение дифференциального уравнения

y ″ − 2 y ′ − 3 y = 0

при следующих начальных условиях

Сначала будем искать общее решение исходного диффе- ренциального уравнения.

k ² e^kx − 2 ke^kx − 3 e^kx = 0,

e^kx (k ² − 2 k − 3) = 0,

e^kx ≠ 0; k ² − 2 k − 3 = 0,

D = 4 − 4⋅(−3) = 16,

Поэтому общее решение исходного дифференциального уравнения имеет вид:

1                 2

y = C e ^{3 x} + C e ^{− x}.

Теперь находим частное решение, соответствующее за- данным начальным условиям. Вначале находим

y ′ = 3 C e ^{3 x} − C e ^{− x},

1               2

затем получаем систему уравнений для нахождения С 1 и С 2.

Поэтому частное решение имеет вид:

y = 2 e ^{3 x} + 6 e ^{− x}.

Пример 6.21.

Найдем общее решение дифференциального уравнения.

y ″ − 6 y ′ + 9 y = 0.

Перепишем исходное дифференциальное уравнение в сле- дующем виде:

k ² e^kx − 6 ke^kx + 9 e^kx = 0,

e^kx (k ² − 6 k + 9) = 0,

e^kx ≠ 0; (k ² − 6 k + 9) = 0,

D = 36 − 4⋅1⋅9 = 0,

Частными решениями данного уравнения являются:

1                                         2

y = e^kx = e ^{3 x} и y = xe^kx = xe ^{3 x}.

Общее решение имеет вид:

1                     2                          1        2

y = C e ^{3 x} + xC e ^{3 x} = e ^{3 x} (C + C x).

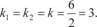
Пример 6.22.

Найдем общее решение дифференциального уравнения

y ″ − 4 y ′ + 13 y = 0.

k ² e^kx − 4 ke^kx + 13 e^kx = 0,

e^kx (k ² − 4 k + 13) = 0,

e^kx ≠ 0; (k ² − 4 k + 13) = 0,

D = 16 − 4⋅1⋅13 = −36,

k 1 = 2 + 3 i; k 2 = 2 − 3 i.

Поэтому общее решение исходного дифференциального уравнения имеет вид:

1                            2

y = e ^{2 x} (C cos 3 x + C sin 3 x).