
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о системах обыкновенных дифференциальных уравнений
(6.52)
Система вида (6.52), правые части которой не содержат производных искомых функций, называется нормальной. Про- интегрировать систему дифференциальных уравнений — зна- чит найти функции y 1, y 2, …, y n,, удовлетворяющие (6.52) и на- чальным условиям
если они заданы. Интегрирование системы (6.52) проводят следующим об- разом.
Дифференцируем по х первое уравнение системы (6.52) и получаем: Заменяя в этом уравнении производные
(6.54)
(6.55)
Подставляем выражения для y 2, y 3, …, y n из (6.55) в послед- нее уравнение системы (6.54) и получаем дифференциальное уравнение n -го порядка для определения y 1, т. е.
Решаем уравнение (6.56) и находим у 1 (6.56) y 1 = ψ1(x, C 1, C 2, …, C n). (6.57)
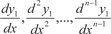 как функции от x, C 1, C 2, …, C n. Затем под- ставляем их в (6.55) и находим искомые функции y 2, y 3, …, y n, т. е. как функции от x, C 1, C 2, …, C n. Затем под- ставляем их в (6.55) и находим искомые функции y 2, y 3, …, y n, т. е.
(6.58)
Для того чтобы полученное решение удовлетворяло задан- ным начальным условиям (6.53) надо найти из (6.57) и (6.58) со- ответствующие постоянные C 1, C 2, …, C n. Теперь приведем конкретный пример решения системы дифференциальных уравнений.
(6.59)
Из второго уравнения системы находим и, подставив в первое уравнение этой системы, получим
или Продифференцируем по t уравнение (6.60):
После преобразований получим:
(6.61)
(6.62) Уравнение (6.62) — это линейное неоднородное дифферен- циальное уравнение второго порядка с постоянными коэффи- циентами, которые рассматривались в п. 6.3.4. Решив уравне- ние (6.62), найдем неизвестную функцию у. Вначале найдем общее решение дифференциального урав- нения без правой части, т. е. y ″ + 4 y ′ + 3 y = 0. Его характеристическое уравнение имеет вид: k 2 + 4 k + 3 = 0; k 1 = −1; k 2 = −3. А общее решение следующее:
где С 1 и С 2 — постоянные. Теперь найдем любое частное решение дифференциаль- ного уравнения (6.62): f (x) = 3cos t − 4sin t. Так как числа ± i не являются корнями характеристическо- го уравнения, то частное решение (6.62) ищем в виде y 2 = A cos t + B sin t, где А и В неизвестные постоянные, которые необходимо опре- делить. Находим y 2′ и y 2″:
или или y 2′ = − A sin t + B cos t y 2″ = − A cos t − B sin t. Поставляем y 2; y 2′; y 2″ в (6.62) и получаем: − A cos t − B sin t − 4 A sin t + 4 B cos t + 3 A cos t + 3 B sin t = = 2cos t − 4sin t 2 A cos t + 4 B cos t + 2 B sin t − 4 A sin t = 2cos t − 4sin t, cos t (2 A + 4 B) + sin t (2 B − 4 A) = 2cos t − 4sin t, 2 A + 4 B = 2 → A = 1, 2 B − 4 A = −4 → B = 0. Следовательно, y 2 = cos t. А общее решение дифференциального уравнения (6.62) имеет вид: y = y 1 + y 2 = C 1 e − t + C 2−3 t + cos t. (6.63)
(6.64)
Дифференцируя по t уравнение (6.63) находим Подставляя в (6.64) найденные значения dy/dt и значение
у из формулы (6.63), получаем искомую функцию х, т. е.
Задачи для самостоятельного решения 1. Найти общие решения дифференциальных уравнений: а) (x + 5) dy − (y + 10) dx = 0; б) (3 xy 2 + 2 x) dx + (2 y + x 2 y) dy = 0; в) г) д) 2 y cos y − sin5 xdy = 0. 2. Предположим, что темп изменения производительности труда характеризуется функцией f (t). Найти функцию произ- водительности труда y = y (t), если:
а) б) 3. Найти общие решения однородных дифференциальных уравнений: а) (y − x) dx + (y + x) dy; б) в) (6 y + 4 x) dx + (3 y + 8 x) dy = 0; г) 4.
а)
в)
г) 5. Найти общие решения дифференциальных уравнений: а) y ′ − 2 y + 7 = 0; б) 3 y ′ − 6 y + 9 = 0. 6. Найти общие решения дифференциальных уравнений: а) y ″ = 5 x; б) y ″ = cos x; в) y ″ = 18 x 2 + 2; г) y ″ = 10 x 2 + 2 x. 7.
 при при
б) y ″ = sin x при 8. Найти общие решения дифференциальных уравнений: а) y ″ − 5 y ′ + 6 = 0; б) y ″ − 3 y ′ + 16 = 0; в) y ″ − 22 y ′ + 12 = 0; г) 6 y ″ − 10 y ′ − 7 = 0; 9. Найти частные решения дифференциальных уравне- ний, удовлетворяющие заданным начальным условиям: а) y ″ + 4 y ′ + 3 = 0, если
10. Найти общие решения дифференциальных уравнений: а) y ″ − 2 y ′ + 2 y = 3 e 4 x; б) y ″ − y ′ − 2 y = e 7 x; в) y ″ + 3 y ′ + 2 y = 4 x 2 − 3 x − 16; г) y ″ + 4 y ′ + 4 y = 3sin 3 x + 2cos 3 x; д) y ″ − 12 y ′ + 36 y = 3sin x; е) y ″ − 4 y ′ − 5 y = cos 3 x. 11.
б)
лах: 12. Найти общее решение уравнений Бернулли: а) б) 13. Проинтегрировать уравнение в полных дифференциа-
а) б) 14. Решить уравнения, допускающие интегрирующий мно- житель вида λ = λ(х) или λ = λ(у): а) б) 15. Найти общие решения следующих дифференциальных уравнений: а) (x − 2 y + 5) dy + (2 x + y − 3) dx = 0; б) (x − y + 7) dy + (x + y − 9) dx = 0. 16. Найти общее решение линейного дифференциального уравнения 17. а)
б) ; в) y · y ″ − (y ′)2 = 0 г) 2(y ′)2 + y · y ″ = yy ′. 18. Найти общее решение дифференциального уравнения y ″ − 4 y ′ + 8 y = e 3x · (x sin x + x 2 · cos x). 19. Найти общее решение следующих дифференциальных уравнений а) y = 5 xy ′ − (ey)′; б) y = x (y ′)2 + 2(y ′)2.
Вопросы для самопроверки 1. Какое дифференциальное уравнение называется диф- ференциальным уравнением первого порядка? 2. Что такое общее решение дифференциального уравне- ния первого порядка? 3. Что такое частное решение и в чем суть начальных усло- вий для дифференциального уравнения первого порядка? 4. Дать формулировку теоремы существования и единс- твенности решения дифференциального уравнения первого порядка. 5. Что является геометрической иллюстрацией общего и час- тного решений дифференциального уравнения первого порядка? 6. Что такое дифференциальное уравнения первого поряд- ка с разделяющимися переменными и каким методом его мож- но решить? 7. Какие дифференциальные уравнения первого порядка называются однородными, каков их метод решения? 8. Какие дифференциальные уравнения первого порядка называются линейными, каков их метод решения? 9. В чем состоит метод Лагранжа решения линейных диф- ференциальных уравнений первого порядка? 10. Какие функции называются однородными функциями
n- го измерения? 11. Как найти общее решение линейного дифференциаль- ного уравнения первого порядка с постоянными коэффициен- тами? 12. Чем отличается задание краевых условий от задания начальных условий в дифференциальных уравнениях второго порядка? 13. Какие дифференциальные уравнения второго порядка с постоянными коэффициентами называются однородными? 14. Как найти общее решение однородного дифференци- ального уравнения второго порядка с постоянными коэффици- ентами? 15. Как найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянны- ми коэффициентами? 16. Что называется системой дифференциальных уравне- ний и ее решением? 17. Как система дифференциальных уравнений сводится к одному дифференциальному уравнению высшего порядка? 18. Какое уравнение называется уравнением Бернулли и каков метод его решения? 19. Какое дифференциальное уравнение первого порядка называется уравнением в полных дифференциалах? 20. Каковы методы решения уравнений в полных диффе- ренциалах? 21. Что такое интегрирующий множитель и каков метод его нахождения?
Глава 7. РЯДЫ Числовые ряды Выражение где w 1, w 2, …, w n, … — некоторые числа, называют числовым ря- дом; w 1, w 2, …, w n, … — это члены ряда. Для любого числового ряда S 1 = w 1; S 2 = w 1 + w 2; S 3 = w 1 + w 2 + w 3; ……………………... S n = w 1 + w 2 + w 3 + … + w n, n = 1, 2, 3, … (7.1)
Приведем конкретные примеры. Пример 7.1. Гармонический ряд Пример 7.2. Геометрическая прогрессия w + wq + wq 2 + … + wqn -1 + … (w 0) сходится при | q | < 1 и расходится при | q | 1. Если | q | < 1, то Пример 7.3. Обобщенно гармонический ряд Пример 7.4.
т. е. данный ряд сходится и его сумма равна (е – 1). При исследовании рядов одним из важнейших вопросов является вопрос о том, сходится изучаемый ряд или расхо- дится. Далее рассмотрим достаточные признаки, на основании которых можно решить этот вопрос. Сейчас же приведем не- обходимый признак сходимости рядов, т. е. условие, при невы- полнении которого ряды расходятся.
Теорема 7.1. Если ряд сходится, то его n- й член стремится к нулю при неограниченном возрастании n. Следствие. Если n- й член ряда не стремится к нулю при n →, то ряд расходится. Данный признак не является доста- точным, т. е. он может выполняться, а ряд будет расходиться. Например, гармонический ряд из примера 7.1 расходится, не- смотря на то, что
Основные свойства сходящихся числовых рядов 1. Сходимость числового ряда не нарушится, если припи- сать или отбросить конечное число его членов. 2. Если члены сходящегося ряда умножить на одно и то же число k, то его сходимость не нарушится. 3. Два сходящихся ряда u 1 + u 2 + … + u n + … = S 1; v 1 + v 2 + … + + v n + … = S 2 можно почленно складывать (или вычитать), так что ряд (u 1 ± v 1) + (u 2 ± v 2) + … + (u n ± v n) + … будет сходится, а его сумма будет равна S 1 ± S 2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.180.161 (0.078 с.) |
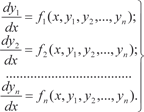
 (6.53)
(6.53)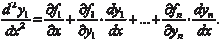
 их вы- ражениями из (6.52) получим дифференциальное уравнение
их вы- ражениями из (6.52) получим дифференциальное уравнение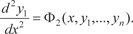
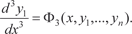
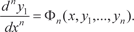
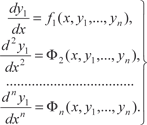
 Из первых (n − 1) уравнений системы (6.54) получаем y 2, y 3, …, y n, выразив их через , т. е.
Из первых (n − 1) уравнений системы (6.54) получаем y 2, y 3, …, y n, выразив их через , т. е.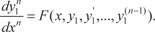
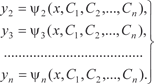
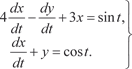
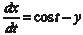
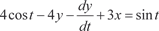
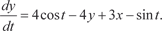 (6.60)
(6.60)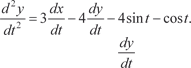
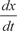
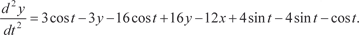



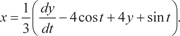
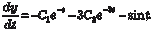
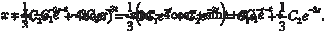

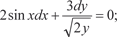
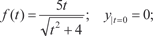
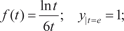



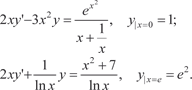 б)
б) 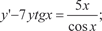

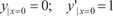
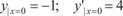

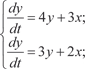

 ;
;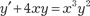 .
. ;
; .
. ;
;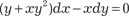 .
.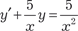 , используя метод Лагранжа. Затем оп- ределить его частное решение, используя следующее началь- ное решение: y = 0; x = 1.
, используя метод Лагранжа. Затем оп- ределить его частное решение, используя следующее началь- ное решение: y = 0; x = 1.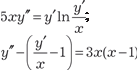 Найти общее решение следующих дифференциальных уравнений:
Найти общее решение следующих дифференциальных уравнений: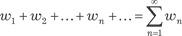 ,
,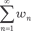 можно построить после- довательность его частичных сумм S n:
можно построить после- довательность его частичных сумм S n:
 расходится.
расходится.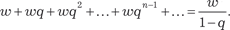 .
. схо- дится при a > 1 и расходится при a 1.
схо- дится при a > 1 и расходится при a 1.
 .
.


