
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
О дифференциальных уравнениях
6.1. Основные понятия и определения Дифференциальными называются уравнения, которые со- держат искомые функции, их производные и (или) дифферен- циалы различных порядков, независимые переменные. Теория дифференциальных уравнений появилась в кон- це XVIII в. в результате решения некоторых задач механики и физики. Термин дифференциальные уравнения ввел Г. Лей- бниц. Дифференциальные уравнения подразделяются на диф- ференциальные уравнения в частных производных, неизвест- ная функция в которых зависит от двух и большего количества неизвестных, и на обыкновенные дифференциальные уравне- ния, неизвестная функция в которых зависит от одного аргу- мента. В данном учебнике кратко рассмотрим обыкновенные диф- ференциальные уравнения. Общий вид обыкновенного дифференциального уравнения следующий: F (x, y, y ′, y ″, …, y ( n )) = 0
Наивысший порядок производных, входящих в дифферен- циальное уравнение, называется его порядком. Например, Решить дифференциальное уравнение — это значит найти такую функцию, подстановка которой в это дифференциаль- ное уравнение превращает его в тождество. Любое дифференциальное уравнение имеет бесконечное множество решений. Геометрически они изображаются се- мейством интегральных кривых. И эту совокупность решений называют общим решением дифференциального уравнения и записывают так: y = ϕ(x, C 1, C 2, …, C n). А решения, содержащие конкретные значения постоян- ных, называются частными решениями дифференциальных уравнений.
Дифференциальные уравнения 1-го порядка Общие понятия Дифференциальное уравнение первого порядка — это уравнение, связывающее независимую переменную, неизвест- ную функцию, ее производную и (или) дифференциал. Его общий вид следующий: F (x, y, y ′) или Если это уравнение можно разделить относительно произ- водной (y ′), то получим одно или несколько уравнений вида: y ′ = f (x, y). Общее решение этого дифференциального уравнения име- ет следующий вид: y = ϕ(x, C).
Задавая начальные условия, из семейства интегральных кривых выделяем какую-то конкретную кривую. Вопрос о том, в каком случае можно утверждать, что час- тное решение дифференциального уравнения, удовлетворяю- щее заданному начальному условию существует, а также явля- ется единственным, становится ясным из следующей теоремы. Теоремы 6.1. Если в дифференциальном уравнении y ′ = f (x, y) функция y = f (x, y) и ее частная производная по y
Приведенная теорема была впервые сформулирована и доказана Коши. Поэтому задачу нахождения частного решения по заданным начальным условиям называют задачей Коши.
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 89; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.244.44 (0.008 с.) |

 это дифференциальное уравне- ние второго порядка.
это дифференциальное уравне- ние второго порядка.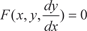 .
.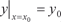
 непрерывны в некоторой области D на плоскости х 0 у, содержащей точку (x 0, y 0), то существует единственное реше- ние этого дифференциального уравнения y = ϕ(x,), удовлетво- ряющее условию при х = х 0 и у = у 0 [44, 59].
непрерывны в некоторой области D на плоскости х 0 у, содержащей точку (x 0, y 0), то существует единственное реше- ние этого дифференциального уравнения y = ϕ(x,), удовлетво- ряющее условию при х = х 0 и у = у 0 [44, 59].


