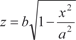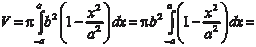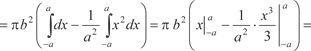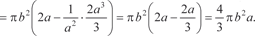Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление площадей плоских фигур
Так как определенный интеграл от непрерывной неотрица- тельной функции равен площади соответствующей криволиней- ной трапеции, а площадь любой плоской фигуры можно пред- ставить как сумму и (или) разность площадей криволинейных трапеций, то, следовательно, определенный интеграл можно ис- пользовать для вычисления площадей плоских фигур [9, 35].
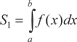 и и
.
y f (x)
S 1
0 a b x Рис. 5.9
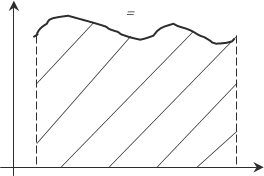
Рис. 5.10 Если функция y = f (x) находится полностью или частично под осью 0 х (рис. 5.11 и 5.12), то получаем:
y f (x) Рис. 5.11
Рис. 5.12 Если функция x = (y) или плоская фигура ABCD прилега- ют к оси 0 y, то (рис. 5.13 и 5.14)
Рис. 5.13
Задачи на вычисление площадей плоских фигур можно решать по следующей схеме: 1) В соответствии с условиями задачи делают схематичес- кий чертеж. 2) Искомую площадь представляют как сумму и (или) раз- ность площадей криволинейных трапеций. 3) Находят пределы интегрирования. 4) Вычисляют площади каждой криволинейной трапеции и искомую площадь фигуры. Теперь рассмотрим конкретные примеры вычисления пло- щадей плоских фигур. Пример 5.40. Вычислите площадь фигуры, ограниченной линиями: х = = 4 − у 2 , х = 0. Сначала по условиям задачи строим схематический чер- теж (рис. 5.15).
Рис. 5.15 x = 4 − у 2 — парабола. Найдем ее вершину х = -2 у. y = 0, х = = 4 (max) и точки пересечения с осью 0 у. 4 − у 2 = 0, у = 2, у = -2. y 1 = -2 и y 2 = 2 являются пределами интегрирования. Теперь найдем искомую площадь. Так как парабола сим-
метрична относительно оси абсцисс, то можно записать.
Пример 5.41. Вычислим площадь фигуры, ограниченной линиями: y = x 2 − 6 x + 8; y = 0. Построим схематический чертеж искомой фигуры (см. рис. 5.16)
Рис. 5.16 Кривая y = x 2 − 6 x + 8 есть парабола, ветви которой на- правлены вверх. Найдем ее характерные точки. y = 2 x − 6; y = 0; 2 x − 6 = 0; x = 3, y = -1 (min); x 2 − 6 x + 8 = 0; D = 36 − 4·1·8 = 4;
так как фигура находится под осью 0 х).
Пример 5.42. Вычислите площадь фигуры, ограниченной линиями xy = 6, x + y − 7 = 0.
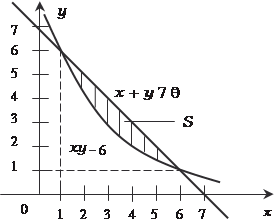
Построим схематический чертеж (рис. 5.17) и найдем пре- делы интегрирования:
(пределы интегрирования)
Рис. 5.17
Теперь находим искомую площадь
= 35 − 17,5 − 6ln6 = (17,5 − 6ln6) кв. ед. Нахождение длины дуги кривой
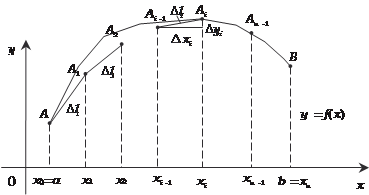
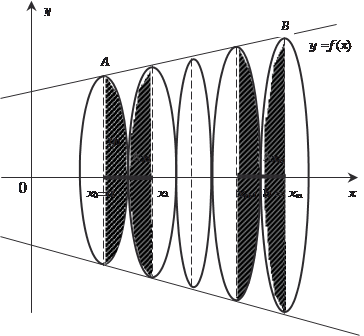
Пусть в плоскости х 0 у уравнением y = f (x) задана кри- вая линия. Вычислим длину дуги АВ этой кривой, заключенной между прямыми х = а и х = b (рис. 5.18). Рис. 5.18 На дуге АВ возьмем точки А, А 1, А 2, …, В с абсциссами х 0 = = а, х 1, х 2, …, b = х n. Проведем хорды АА 1, А 1 А 2, …, А n -1 В, длины которых соответственно обозначим l 1, l 2, …, l n. В результате получим ломаную линию А А 1 А 2 … А n -1 В, которая вписана в
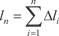 . А длиной (l) дуги АВ называется предел, к которому стремится длина впи- санной ломаной, когда длина ее наибольшего звена стремится к нулю, т. е. . А длиной (l) дуги АВ называется предел, к которому стремится длина впи- санной ломаной, когда длина ее наибольшего звена стремится к нулю, т. е.
(5.14) Рассмотрим конкретный пример. Пример 5.43 Найти длину дуги кривой Сначала построим график исходной функции и найдем а и b (рис. 5.19)
Теперь по формуле (5.14) нахо- дим искомую длину дуги.
x Рис. 5.19 Найдем
 — гиперболический синус) или методом интегри- рования по частям, которым мы и воспользуемся. Напомним, что формула интегрирования по частям имеет вид: — гиперболический синус) или методом интегри- рования по частям, которым мы и воспользуемся. Напомним, что формула интегрирования по частям имеет вид:
.
Тогда получим:
В нашем случае получаем
Поэтому l 1 примет вид:
. Объем тела вращения
Рассмотрим тело, которое образовано вращением вокруг оси 0 х криволинейной трапеции aABb, ограниченной функцией y = f (x), осью 0 х и прямыми x = a и x = b (рис. 5.20). Рис. 5.20
= y 2 i-1 x i, [в данном случае поперечные сечения с абс- циссами x 0 = a, x 1, …, x n -1, x n = b есть окружности].
Поэтому объем n-ступенчатого тела будет равен: Переходим к пределу при n → и при стремлении max x i → 0 и получаем искомый объем тела вращения [9]:
В том случая, если тело образовано вращением вокруг оси 0 у криволинейной трапеции cCDd, ограниченной функцией х = (у) и прямыми у = с, у = d (рис. 5.21), то его объем находит- ся по формуле
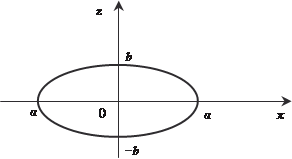
Рис. 5.21 Теперь рассмотрим конкретный пример. Пример 5.44. Найдем объем двухосного эллипсоида вращения, канони- ческое уравнение которого имеет вид большая и малая полуоси соответственно (одной из моделей Земли как раз и является двухосный эллипсоид вращения, в России принят рефенц-эллипсоид с параметрами а = 6378245 м,
(рис. 5.22).
оси 0х функции , ограниченной прямыми х = - а и х = а, и осью 0 х.
Рис. 5.22
Тогда по формуле (5.15) получаем:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.69.255 (0.028 с.) |
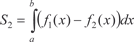
 y
y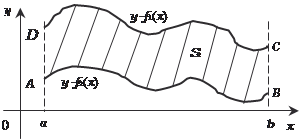

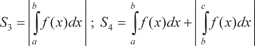 .
.
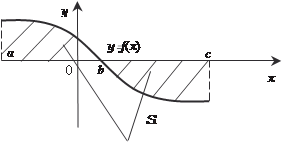
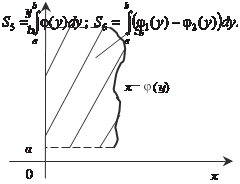
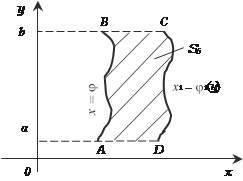
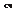 Рис. 5.14
Рис. 5.14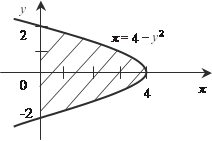
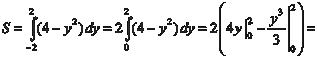
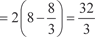 кв. ед.
кв. ед.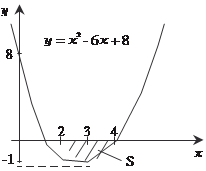
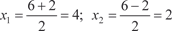 (пределы интегрирования). Теперь находим искомую площадь (знак модуля ставится,
(пределы интегрирования). Теперь находим искомую площадь (знак модуля ставится,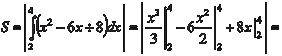
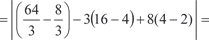
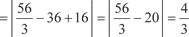
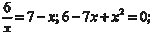
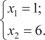
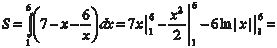

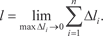
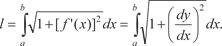
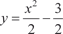 , отсеченной осью 0 х.
, отсеченной осью 0 х.
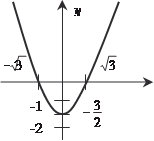 Находим а и b.
Находим а и b.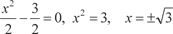
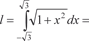 [Так как исходная
[Так как исходная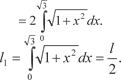 парабола симметрична относительно оси 0у, то получаем]
парабола симметрична относительно оси 0у, то получаем]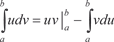
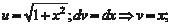
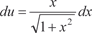
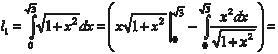
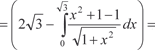
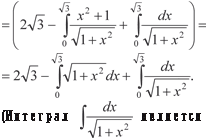
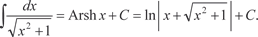
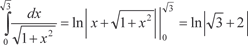 .
.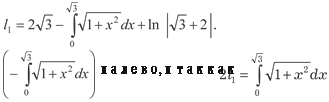
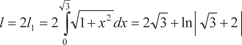
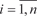
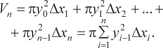
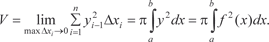 (5.15)
(5.15)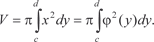 (5.16)
(5.16)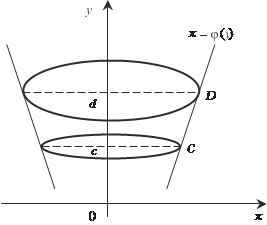
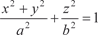 , где а и b —
, где а и b —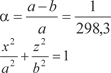 ). Его сечением, в плоскости х 0 z будет эллипс:
). Его сечением, в плоскости х 0 z будет эллипс: