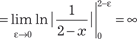Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл второго рода
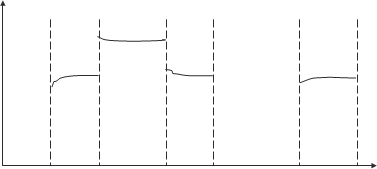
Если на отрезке [ а, b ] функция у = f (х) имеет конечное количество точек разрыва первого рода, то дать определение интеграла для такой функции легко. В этом случае искомый интеграл есть сумма определенных интегралов, взятых по час- тичным интервалам, на которые разбивается отрезок [ а, b ] все- ми точками разрыва функции а < с 1 < с 2 … < с n < b, где с 1 с 2….. с n точки разрыва. Тогда будем иметь Таким образом, мы дали определение площади криво- линейной трапеции, соответствующей функции у = f (х) с ко- нечным числом точек разрыва первого рода на отрезке [ а, b ] (рис. 5.5). Площадь этой трапеции есть сумма площадей трапеций, опирающихся на частичные интервалы [ а 1, с 1], [ с 1, с 2], ….[ с n, b ].
0 а с 1 с 2 с 3 с n b х Рис. 5.5 Распространим определение интеграла на функции с бес- конечными разрывами. Пусть функция у = f (х) непрерывна для всех значений а ≤ х < b, но в точке b имеет бесконечный разрыв (рис. 5.6).
Рис. 5.6 Поэтому определение интегралa в точке b теряет свой смысл. Но если взять обычный интеграл Устремим ε к нулю, тогда I либо имеет предел, либо не име- ет его (стремится к бесконечности либо не стремится ни к како- му пределу, колеблется). Определение. Несобственным интегралом от функции у = f (х), непрерывной при а ≤ х < b и неограниченной при х → b, называется предел интеграла
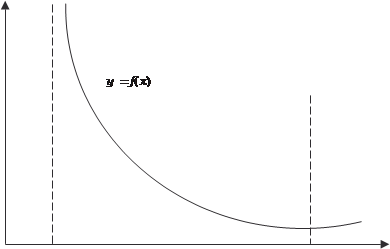
. Если данный предел существует, то несобственный интег- рал сходится, а если не существует, то расходится. Аналогично дается определение несобственного интеграла в том случае, если функция у = f (х) терпит бесконечный раз- рыв в левом конце отрезка интегрирования [ а, b ] (рис. 5.7).
0 а b х В этом случае имеем Рис. 5.7
.
В том случае, если функция у = f (х) терпит бесконечный разрыв в какой-то промежуточной точке х = с отрезка интегри- рования [ а, b ], а < с < b (рис. 5.8), то согласно определению имеем
у 0
Рис. 5.8 Если оба интеграла в правой части последнего равенства сходятся, то сходится и интеграл
Если хотя бы один из интегралов в правой части расходит- ся, то расходится и исходный интеграл. Теперь рассмотрим конкретные примеры. Пример 5.38.
Некоторые приложения определенного интеграла
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 87; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.139 (0.005 с.) |
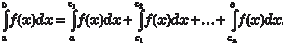
 у
у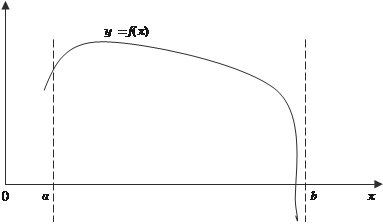 у
у , то можно считать, что функция у = f (х) с уменьшением ε будет все лучше выражать ту величину, которую нужно взять в качестве интеграла от функции у = f (х) на отрезке [ а, b ].
, то можно считать, что функция у = f (х) с уменьшением ε будет все лучше выражать ту величину, которую нужно взять в качестве интеграла от функции у = f (х) на отрезке [ а, b ].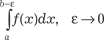 .
.
 у
у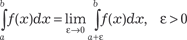


 .
. .
. — интеграл схо- дится.
— интеграл схо- дится.