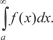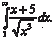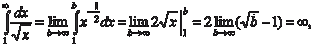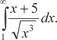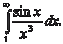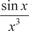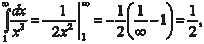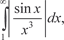Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл первого рода
Распространим понятие определенного интеграла на слу- чай бесконечного интервала интегрирования. Предположим, что функция y = f (x) непрерывна на интер- вале [ a, +). Тогда можно найти интеграл от функции f (x), ко- торый взят по любому интервалу [ a, b ], где b > a. Интеграл Пусть b неограниченно возрастает, тогда есть две возмож- ности: или Теперь дадим определение несобственного интеграла.
[ a, +) называется предел интеграла при b →. Это за- писывается следующим образом
Если предел (5.13) существует, то несобственный интеграл называется сходящимся, а если не существует, то расходя- щимся.
Если первообразная функция F (x) для подынтегральной функции f (x) известна, то можно определить, сходится несобс- твенный интеграл или нет. Используем формулу Ньютона- Лейбница и получим: Поэтому если предел первообразной F (x) при x → + су- ществует, то несобственный интеграл сходится, а если предел не существует, то интеграл расходится.
Аналогично определяется несобственный интеграл в ин- тервале (-; b): Если функция f (x) определена и непрерывна в интервале (-; +), то получим
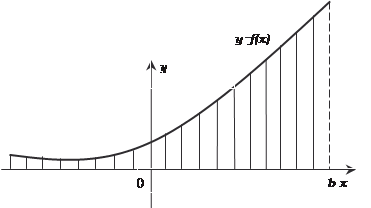
Сходящиеся несобственные интегралы имеют опреде- ленный геометрический смысл. Например, график функции y = f (x) ограничивает криволинейную трапецию с бесконечным основанием (рис. 5.4). Если несобственный интеграл Теперь приведем конкретные примеры решения несобс- твенных интегралов.
Вычислим
Рис. 5.4 [Делаем замену переменной
Пример 5.35.
рал расходится. Пример 5.36. т. е. данный интег-
т. е. данный интеграл расходится. Часто важно знать не конкретное значение несобственного интеграла, а сходится он или расходится. Для этого использу- ются признаки сравнения, которые мы и приводим. 1.
Если для x (x a) выполняется неравенство 0 f (x) (x) и если  сходится, то сходится и сходится, то сходится и 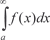 , при этом выпол- няется неравенство , при этом выпол- няется неравенство
Например, проверим сходится ли интеграл
При х 1,
Теперь рассмотрим, сходится ли несобственный интеграл: т. е. данный интеграл сходится. Поэтому по признаку 1 сходит- ся 2. Если для x (x a) выполняется неравенство 0 (x) f (x), причем
Например, проверим сходимость интеграла
Теперь рассмотрим сходится ли несобственный интеграл т. е. данный интеграл расходится. Поэтому по признаку 2 рас- ходится
3.
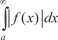 сходится, то схо- дится и интеграл сходится, то схо- дится и интеграл 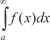 . Последний интеграл в этом случае называется абсолютно сходящимся. . Последний интеграл в этом случае называется абсолютно сходящимся.
В качестве примера проверим сходимость интеграла На интервале [1;) подынтегральная функция знако- переменная.
несобственный интеграл т. е. данный интеграл сходится. Поэтому по признаку 1 сходится
а, следовательно, по признаку 3 сходится и интеграл При использовании признаков сравнения надо иметь запас функций, несобственные интегралы от которых или сходятся, или расходятся и результат этот нам известен заранее. Эти функции мы будем использовать в качестве (х).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.254.133 (0.01 с.) |
 тем лучше выражает значение, которое надо принять в качестве интеграла от функции f (x) в интерва- ле [ a, +), чем больше b.
тем лучше выражает значение, которое надо принять в качестве интеграла от функции f (x) в интерва- ле [ a, +), чем больше b.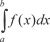 при b → + имеет предел, или данный ин- теграл предела не имеет, а это означает, что он или стремится к бесконечности, или колеблется, т. е. не стремится ни к какому пределу.
при b → + имеет предел, или данный ин- теграл предела не имеет, а это означает, что он или стремится к бесконечности, или колеблется, т. е. не стремится ни к какому пределу.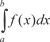
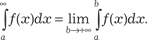
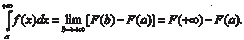
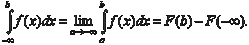

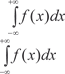 Если оба интеграла в правой части последнего выражения сходятся, то интеграл сходится, а если хотя бы один из
Если оба интеграла в правой части последнего выражения сходятся, то интеграл сходится, а если хотя бы один из
 сходится, то за- штрихованная фигура имеет площадь, которая равна этому интегралу. А если интеграл расходится, то говорить о площади фигуры нельзя.
сходится, то за- штрихованная фигура имеет площадь, которая равна этому интегралу. А если интеграл расходится, то говорить о площади фигуры нельзя.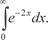
 Затем меняем пределы интегрирования y (0) = 0; y () = -.] Тогда получим
Затем меняем пределы интегрирования y (0) = 0; y () = -.] Тогда получим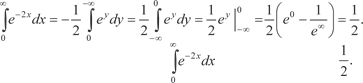 т. е. несобственный интеграл сходится и равен
т. е. несобственный интеграл сходится и равен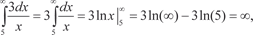
 Величина не стремится к определенному пределу при b → (колеблется).
Величина не стремится к определенному пределу при b → (колеблется).
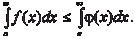
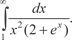
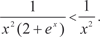
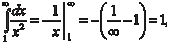
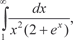 и его значения меньше 1.
и его значения меньше 1.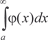 расходится, то расходится и
расходится, то расходится и