
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о методе наименьших квадратов
При обработке результатов наблюдений в естественных, технических и гуманитарных науках часто приходится пользо- ваться эмпирическими формулами, составленными на основа- нии наблюдений. Один из способов получения таких формул — метод наименьших квадратов (МНК). В 1806 г. французский математик Лежандр предложил способ для решения неопреде- ленных СЛАУ, неизвестными в которых являются поправки в результаты наблюдений. Этот способ получил название МНК. В данном способе уравнения подчиняются дополнительно- му условию − сумма квадратов поправок (V), вводимых в рав- ноточные наблюдения, должна быть минимальной, меньше суммы квадратов любой другой системы поправок, удовлетво- ряющей исходным уравнениям, т. е.
Условие (4.14) — это математическое выражение принци- па МНК [54]. Например, мы хотим установить зависимость между дву- мя величинами х и у, где х — административные правонару- шения, а у − преступления. Данные, собранные юридической статистикой, свидетельствуют о наличии неполной прямой линейной зависимости между административными правонару- шениями и преступлениями [36]. То есть в этом случае естест- венно считать, что у это линейная функция от х, записываемая следующим образом:
где а и b − неизвестные коэффициенты; х − измерения;
Исходные данные наблюдений удобно представить в виде табл. 4.1. Таблица 4.1
Причем значения у i, где
Данную функцию можно рассматривать как функцию двух аргументов а и b. Необходимыми условиями минимума этой функции будут равенства
ментов). Далее имеем:
После преобразований получаем так называемую систему нор- мальных уравнений: Решая данную, систему находим искомые коэффициенты:
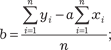 (4.16) (4.16)
(4.17)
Пример 4.34 [36]. Пусть заданы два ряда наблюдений, характеризующих за шесть лет количество хищений оружия (х) и вооруженные пре- ступления (у). Эти деяния связаны между собой потому, что у них почти одни и те же причины. Исходные данные поместим в табл. 4.2, причем заполнять ее будем по возрастанию ряда х.
Таблица 4.2
В данном случае связь между у и х будем искать в виде
По формулам (4.16) и (4.17) находим искомые коэффициен- ты b = -13996; а = 22. Тогда получим ния ряда Используя МНК можно находить коэффициенты и для случая любой нелинейной зависимости двух величин, а также для случая многофакторной зависимости, т. е. исходная функ- ция будет зависеть от нескольких аргументов, причем она мо- жет быть и линейной, и криволинейной. Например, если связь
циенты а 1, а 2, b находятся в результате решения системы нор- мальных уравнений:
Задачи для самостоятельного решения 1. Найти производные следующих функций:
1.2. 1.3.
1.5. 1.6. 2. Найти вторые производные следующих функций: 2.1. y = 6 x 4 + 4sin 3 x; 2.2. y = e 7 x · tg 5 x; 2.3. 2.4. y = 5 x 8 − 16 x 5 + sin 2 x 3. Исследовать функции и построить их графики: 3.1. y = 2 x 4 − 8 x 2 + 3; 3.2. 3.3. y = 2 x 2 − 10; 3.4. y = 2 x 3 − 9 x 2 + 15 x − 6; 3.5. y = 3 x − x 3; 3.6. 4. Найти 4.1. Z = x 3 · sin2 y; 4.2. Z = xy; 4.3. 4.4 Z = tg2 (x 3 y) · 22 x +3; 4.5. Z = arctg (x 4 + 5 y 6); 4.7. 5.Используя правило Лопиталя, найти пределы функций: 5.1. 5.2. 5.3. 5.4. 5.5. 5.6. 6. Найти производную функции
правлению к точке В (0, 1, -2, 4, 3). 7. Найти наибольшую скорость возрастания функции
8. Найти вторые частные производные функций: 8.1. Z = 5 х 3 у 8 – 7ln2 y · sin x; 8.2. Z = 16 tg y · х 5+2 х 7 у 6. 9. Найти производные третьего порядка для функций: 9.1. 9.2. 10. Результаты измерения величин х и у заданы в таблице
Полагая, что между х и у существует линейная зависи- мость вида 11. Найти экстремумы функции двух аргументов. 11.1. Z = 6 – x 2 – (у 2 – 5)2; 11.2. Z = 7(х – у) – 2 x 2 – 3 у 2; 11.3. 12. Найти производную функцию y, если она задана урав- нением. 12.1. еxy + y cos (2 x) +5 – 26 = 0; 12.2. 2 x 3 y 2 – 4 xy + 7 = 0. 13. Найти вторую производную функции y, если она зада- на уравнением: 13.1. 6 xy 2 – 7 yx = 0; 13.2. x 3 – y 3 = 72.
Вопросы для самопроверки 1. Что понимают под неявным заданием функции? 2. Как вычислить производную функции заданной не- явно? 3. Каким образом находятся производные высших поряд- ков от функции, заданной неявно? 4. Дать определение производной функции y = f (x). 5. Каковы геометрический и механический смыслы произ- водной? 6. Как найти производную сложной функции? 7. Дать определение дифференциала функции y = f (x). 8. Какой геометрический смысл имеет дифференциал? 9. Что называется производной второго порядка от функ- ции y = f (x)? 10. В чем состоит достаточный признак экстремума? 11. Какие точки называются точками перегиба функции y = f (x)? 12 Что называется асимптотой функции y = f (x)? 13. Сформулировать правило Лопиталя и привести приме- ры его применения. 14. Что называется функцией двух независимых пере- менных? 15. Что называется графиком функции двух независимых переменных? 16. Что называется пределом функции Z = f (x, y) при x → x 0 и y → y 0. 17. Дать определение частных производных функции двух независимых аргументов. 18. Дать определение градиента 19. Как можно выразить производную по направлению че- рез градиент? 20. Что называется частной производной второго порядка от функции двух независимых аргументов? 21. Дать формулировку теоремы о равенстве вторых сме- шанных частных производных. 22. Что называется производной n-го порядка от заданной функции? 23. В чем состоит суть МНК? 24. Как с помощью МНК находить коэффициенты эмпири- ческих формул? 25. Дать определение точки экстремума функции двух ар- гументов. 26. В чем состоит необходимый признак экстремума функ- ции двух аргументов. 27. В чем состоят достаточные условия экстремума функ- ции двух аргументов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 74; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.102.223 (0.03 с.) |
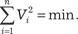
 = ах + b, (4.15)
= ах + b, (4.15)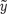 − теоретические значения показателя, лежащие точно на прямой линии.
− теоретические значения показателя, лежащие точно на прямой линии. не обязательно точно лежат на прямой линии.
не обязательно точно лежат на прямой линии.
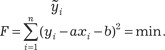 подставляем в него вместо его значение из (4.15) и получаем
подставляем в него вместо его значение из (4.15) и получаем

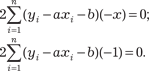
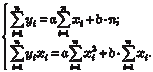
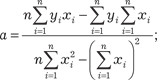

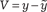

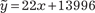 . (14.18) Используя формулу (4.18), найдем выравненные значе-
. (14.18) Используя формулу (4.18), найдем выравненные значе- . Они приведены в третьей строке табл. 4.2, в ней же в четвертой графе показаны поправки.
. Они приведены в третьей строке табл. 4.2, в ней же в четвертой графе показаны поправки.
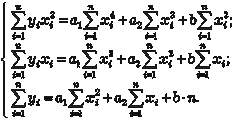
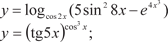 1.1. ;
1.1. ;
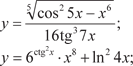 1.4.
1.4.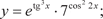

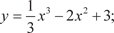
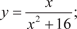
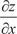 и
и 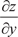 , если функция Z имеет вид:
, если функция Z имеет вид: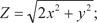
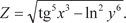
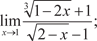
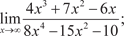


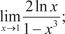
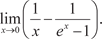
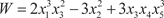 в точке А (0, -1, 2, 4, -3) по на-
в точке А (0, -1, 2, 4, -3) по на- в точке А (-2, -1, 3, 0, 4).
в точке А (-2, -1, 3, 0, 4). ;
; .
. с помощью МНК найти коэффициенты а и b.
с помощью МНК найти коэффициенты а и b.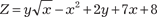 .
.


