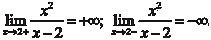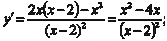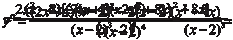Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функций с помощью производных первого и второго порядков, построение их графиков
Приведем ряд теорем, позволяющих находить участки монотонности (возрастания, убывания) функции, экстремумы функции, участки выпуклости и вогнутости функции и точки перегиба. Вначале сформулируем достаточный признак монотон- ности: 1) если f (x) > 0 на некотором интервале, то f (x) на этом интервале возрастает; 2) если f (x) < 0 на некотором интервале, то f (x) на этом интервале убывает; 3) если f (x) = 0 на некотором интервале, то f (x) на этом интервале постоянна.
Рис. 4.8
Важную роль в исследовании функций играют точки, от- деляющие интервалы ее возрастания от интервалов ее убы- вания. Эти точки носят название экстремумов функции или ее локальных максимумов и минимумов. Слово “локальный” оз- начает, что точка будет максимальной (минимальной) лишь на каком-то интервале. Теперь приведем определение: 1) точка M (x 1, y 1) есть точка локального максимума фун- кции y = f (x), если f (x 1) — наибольшее значение функции y = f (x) в некоторой окрестности точки M (x 1, y 1); 2) точка N (x 2, y 2) есть точка локального минимума функции y = f (x), если f (x 2) — наименьшее значение функции y = f (x) в некоторой окрестности точки N (x 2, y 2). Функция на своей области определения может иметь не- сколько экстремумов. Наибольшее и наименьшее значения функции ее области определения обычно называют абсолют- ным максимумом и абсолютным минимумом. Понятие экстремума функции иллюстрируется рис. 4.9. Теперь сформулируем необходимый признак экстремума:
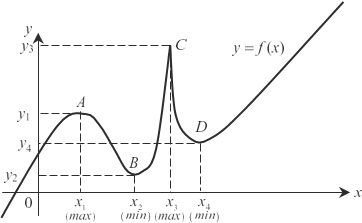
Если в точке (т. А, т. В, т. С, т. D на рис. 4.9) функция y = f (x) дости- гает экстремума, то ее производная в этой точке либо равна нулю (т. А, т. В, т. D на рис. 4.9), либо не существует (т. С на рис. 4.9). Рис. 4.9 Приведенный признак не является достаточным, т. е. из того факта, что производная в данной точке равна нулю или не сущес- твует, еще не следует, что эта точка есть экстремум функции. Недостаточность данного признака проиллюстрируем примером. Пример 4.27. Рассмотрим функцию y = x 3 и найдем ее экс- тремум, используя приведенный признак (найдем производ- ную данной функции, приравняем ее к нулю и найдем коорди- наты экстремума, если он существует).
соответствии с необходимым признаком. Но из графика функции y = x 3 (рис. 4.10) следует, что экстре- мума в точке с координатами х = 0, у = 0 у данной функции нет.
Рис. 4.10 Сформулируем теперь достаточный признак экстремума: точка (т. А, т. В, т. С, т. D на рис. 4.9) есть точка экстремума фун- кции y = f (x), если производная этой функции y = f (x) при переходе х через критическую точку (точку, где производная равна нулю или не существует) меняет знак. Если знак меняет- ся с плюса на минус (т. А, т. С на рис. 4.9), то имеем локальный максимум, а если знак меняется с минуса на плюс (т. В, т. D на рис 4.9), то имеем локальный минимум. Заметим, что функция y = f (x) должна быть непрерывна на интервале, содержащем критическую точку.
Пример 4.28. Производная функции меняет знак при переходе через точку х = 0, но экстремума в ней не имеет, так как в этой точке она разрывна [9]. Вернемся к примеру 4.27 и проверим, удовлетворяется ли там достаточный признак экстремума (рис. 4.11).
 Рис. 4.11 Рис. 4.11
Из рисунка видно, что производная функции y = x 3 не меня- ет знака при переходе х через точку х = 0, поэтому данная фун- кция не имеет экстремума в точке с координатами х = 0, у = 0. Пример 4.29. Рассмотрим функцию y = 3 x 3 + 6 x 2 - x + 2. y = 9 x 2 + 12 x - 1 9 x 2 + 12 x - 1 = 0
y = 9(x - 0,06)(x + 1,4) Применяя достаточный признак экстремума, находим, что в точке х = -1,4 — максимум, а в точке х = 0,06 — минимум (рис. 4.12).
Точки экстремума можно находить и с помощью второй производной. Для этого сформулируем второй достаточный при- знак экстремума: некоторая точка с координатами x 0, y 0 будет точкой экстремума функции y = f (x), если f (x 0) = 0, а f (x 0) 0, при этом, если f (x 0) > 0, то данная точка будет точкой минимума функции y = f (x), а если f (x 0) < 0 — точкой максимума; в том случае если f (x 0) = 0 данный признак не применим. Используем приведенный признак для нахождения экс- тремумов функции y = 3 x 3 + 6 x 2 − x + 2 из примера 4.29. y = 18 x + 12. y (x = 0,06) = 18 · 0,06 + 12 13,1. y (x = -1,4) = 18 · (-1,4) + 12 -13,2.
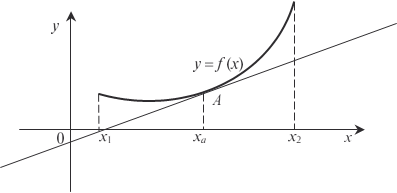
Следовательно, в точке х = 0,06 исходная функция будет иметь минимум, а в точке х = -1,4 — максимум. Теперь покажем, как применять вторую производную для нахождения участков выпуклости и вогнутости функции и ее точек перегиба. Сначала приведем соответствующие определения. График дифференцируемой функции y = f (x) называется вогнутым вверх (в положительном направлении оси ординат) на некотором интервале, если на этом интервале он располо- жен выше касательной, проведенной к любой точке графика в этом интервале (рис. 4.13).
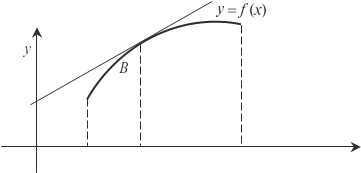
Рис. 4.13 График дифференцируемой функции y = f (x) называется выпуклым вверх (в положительном направлении оси ординат) на некотором интервале, если на этом интервале он располо- жен ниже касательной, проведенной к любой точке графика в этом интервале (рис. 4.14). Точки, отделяющие участки выпуклости функции от учас- тков ее вогнутости (и наоборот), называются точками перегиба. Теперь сформулируем теорему. Теорема 4.6. Если вторая производная функции y = f (x) всюду на некотором интервале меньше нуля, то функция y = f (x) на этом интервале — выпуклая; если вторая производ-
ная функции y = f (x) всюду на некотором интервале больше нуля, то функция y = f (x) на этом интервале — вогнутая. Приведем также необходимый признак существования точ- ки перегиба: если точка с координатами x 0, y 0 является точкой перегиба функции y = f (x), то вторая производная данной фун- кции в этой точке либо равна нулю, либо не существует. Недостаточность данного признака мы проиллюстрируем примером. Пример 4.30. Рассмотрим функцию y = x 4. Воспользовав- шись приведенным выше признаком, проверим, есть ли у этой функции точки перегиба.
Рис. 4.15 должна быть точкой перегиба по необходи- мому признаку, но если взгля- нуть на график этой функции (рис. 4.15) видно, что в данной точке перегиба нет.
при переходе х через x 0; если знак меняется с минуса на плюс, то слева от данной точки лежит участок выпуклости, а спра- ва — участок вогнутости, а если знак меняется с плюса на ми- нус, то наоборот. Применим данный признак к функции из примера 4.30. Из рис. 4.16 видно, что достаточный признак не выполняет- ся, поэтому в точке с координатами х = 0, у = 0 перегиба нет.
Рис. 4.16 Теперь применим достаточный признак существования точки перегиба к функции из примера 4.29.
тельствует о том, что точка с абсциссой является точкой перегиба функции y = 3 x 3 + 6 x 2 - x + 2.
 Рис. 4.17 Рис. 4.17
y = 18 x + 12; 18 x + 12 = 0; Теперь приведем схему, по которой удобно проводить ис- следование функций [9]: 1. Нахождение области определения функции, точек ее раз- рыва, интервалов ее непрерывности и вертикальных асимптот. 2. Проверка функции на четность, нечетность, периодич- ность. 3. Нахождение точек пересечения графика функции с ося- ми координат (если это не требует больших вычислительных затрат).
4. Нахождение интервалов монотонности и точек экстре- мума функции. 5. Нахождение участков выпуклости, вогнутости функции и точек ее перегиба. 6. Нахождение наклонных асимптот. 7. Построение графика функции по результатам прове- денного исследования. Пример 4.31. Теперь в соответствии с приведенной схемой исследуем функцию
Данная функция определена на всей оси 0 х за исключени- ем точки х = 2, т. е. x (-; 2) (2; +). Прямая х = 2 является вертикальной асимптотой данной функции, так как Функция не является ни четной, ни нечетной, ни периоди- ческой, так как f (- x) f (x), f (- x) - f (x), f (x + T) f (x), где Т — период, а график данной функции проходит через начало координат. Теперь найдем первую производную исходной функции и найдем участки монотонности и экстремумы.
x 2 - 4 x = 0; x (x - 4) = 0; x = 0; x = 4. Точку х = 2, где не существует первой производной исход- ной функции, на экстремум можно не проверять, так как в этой точке сама функция имеет бесконечный разрыв. Следовательно (рис. 4.18), в соответствии с достаточным признаком экстремума данная функция имеет максимум в точ- ке с координатами х = 0, у = 0 и минимум в точке с координата- ми х = 4, у = 8.
Рис. 4.18
Теперь найдем вторую производную и определим участки вогнутости, выпуклости и точки перегиба, используя теоре- му 4.6 и достаточный признак существования точки перегиба
Таким образом, вторая производная нигде не обращается в ноль, следовательно, данная функция не имеет точек переги- ба. Надо только проверить, меняет ли вторая производная ис- ходной функции знак при переходе х через точку бесконечного разрыва х = 2 (второй производной заданной функции также не существует в точке х = +2).
Рис. 4.19 Теперь проверим, имеет ли исходная функция наклонные асимптоты, для этого воспользуемся формулами (4.12) и (4.13) (так как заданная функция является дробно-рациональной, можно рассматривать произвольное стремление х к бесконеч- ности).
Поэтому прямая у = х + 2 является наклонной асимптотой исходной функции.
 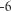 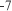  Теперь по результатам проведенного исследования пост- роим график заданной функции (рис. 4.20). Теперь по результатам проведенного исследования пост- роим график заданной функции (рис. 4.20).
Рис. 4.20
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.49 (0.058 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

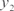
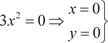

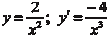




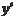





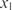



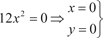

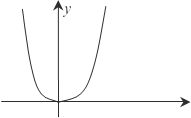




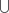
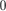




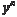




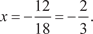
 .
.