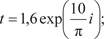Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел последовательности. Предел функции. Вычисление пределов
Прежде чем перейти к определению предела напомним, что в математике используются три вида бесконечностей +, -,. Бесконечность не является числом, она показывает, как меняется переменная величина, которая конечна в любой мо- мент времени. Теперь определим понятие последовательности и ее пре- дела. Последовательностью называется множество чисел, ко- торое перенумеровано с помощью целых чисел и расположено в порядке возрастания номеров.
Например, члены геометрической прогрессии
Может случиться так, что с увеличением n значения y n = = f (n) будет неограниченно приближаться к какому-то числу a. В этом случае говорят, что число a является пределом функции f (n) целочисленного аргумента n или последовательности y 1, y 2, …, y n … при n →, и пишут Число a является пределом последовательности y 1, y 2, …, y n, …, если для > 0 можно найти такое N > 0, что для всех f (n) с номерами n > N справедливо неравенство | f(n) − a | < . (3.2) Используя приведенное определение, докажем, что после- довательность
Таким образом, мы доказали, что для любого наперед за- данного > 0 можно найти такое, что при всех n > N будет выполняться (3.2), а это означает, что 1 есть предел ис- ходной последовательности.
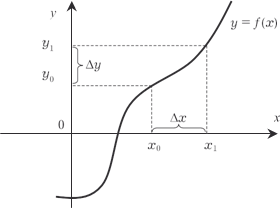
Теперь рассмотрим функцию y = f (x) непрерывного аргу- мента x (рис. 3.24) и предположим, что x неограниченно при- ближается к числу x 0 (x → x 0). При этом может оказаться, что соответствующее значение f (x) неограниченно приближается к некоторому числу b. В этом случае говорят, что число b есть предел функции f (x) при (x → x 0). Рис. 3.24 Сформулируем определение предела функции. Число b называется пределом функции y = f (x) при x → x 0, если для > 0 можно найти такое > 0, что для всех x x 0, удовлетворяющих условию | x − x 0| <, будет спра- ведливо неравенство: | f (x) − b | <. Заметим, что функция не обязательно должна быть определена в предельной точке х 0, она должна быть определена лишь в некоторой окрестности этой точки.
Тот факт, что b — предел функции y = f (x) при x → x 0 за- писывается так:
На основании определения имеем
Таким образом, мы доказали, что исходная функция будет отличаться от 6 меньше, чем на, если будет выполняться не- равенство (3.3). В данном случае =. Приведенное определение не дает способа вычисления пределов. Ниже мы рассмотрим некоторые из таких методов. Дадим понятие о левых и правых пределах функции y = f (x) и точках ее разрыва.
Геометрическая иллюстрация левого и правого пределов дана на рис. 3.25.
Рис. 3.25 Из рис. 3.25 следует, что в точке x 0 функция y = f (x) имеет разрыв. Он носит название разрыва первого рода (в точке раз- рыва первого рода левый и правый пределы не равны b 1 b 2 и конечны). Все остальные точки разрыва называются точками
разрыва второго рода. Примерами разрывов второго рода яв- ляются бесконечные разрывы (рис. 3.26).
Рис. 3.26 Предположим, что аргумент функции y = f (x) неограни- ченно возрастает x →, т. е. является бесконечно большим ар- гументом. Может оказаться, что при этом функция f (x) стре- мится к некоторому пределу b (рис. 3.27). Функция y = f (x) стремится к пределу b при x →, если
для > 0 можно найти такое N > 0, что для всех значений x, удовлетворяющих неравенству | x | > N, будет выполняться ус- ловие | f (x) − b | <. Рис. 3.27 Теперь рассмотрим случай стремления функ- ции y = f (x) к бесконечности при x → x 0. Функция y = f (x) стре- мится к бесконечности при x → x 0, если для M > 0 можно найти такое > 0, что для всех значений x x 0, удовлетворяющих условию | x − x 0| <, выполняется не- равенство | f (x)| > M.
Это определение ил- люстрируется рис. 3.28. Напомним, что функ- ция y = f (x) называется ог- раниченной в данной облас-
ти изменения аргумента, если существует N > 0 такое, что для всех значений х, принадлежащих рассматриваемой области, будет выполняться неравенство | f (x)| N. Если такого числа N нет, то функция y = f (x) является неограниченной в данной об- ласти. Например, функция y = sin x является ограниченной на своей области определения x (−; +) (рис. 3.29).
Рис. 3.29 |sin x| 1, т. е. N = 1. Дадим определение бесконечно малой величины. Функция (х) называется бесконечно малой при х → х 0 или
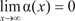 . .
Например, функция y = (x − 3)3 при х → 3 есть бесконечно малая величина, так как Постоянное очень малое число не является бесконечно ма- лой величиной. Единственное число, которое рассматривается в качестве бесконечно малой величины, это ноль. Связь беско- нечно малых и бесконечно больших величин можно проследить из теоремы 3.1: если (x) — бесконечно малая величина, то
Например, .
Если , то (x) есть бесконечно малая более низ- кого порядка, чем (x).
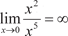 . .
Например, .
Например, . Теперь приведем основные свойства пределов, которые будем использовать при их вычислении. 1.
Предел алгебраической суммы конечного числа функции равен алгебраической сумме пределов от этих функций, т. е. 2. Предел постоянной величины равен самой постоянной величине, т. е.
3.
Предел произведения конечного числа функций равен произведению пределов от этих функций, т. е. Следствие Постоянный множитель можно выносить за знак предела, т. е.
где C R. 4.
Предел частного двух функций равен частному от их пределов, если предел знаменателя не равен нулю, т. е. 5. Предел целой положительной степени функции равен той же степени предела этой функции, т. е.
где n Z +, Z + — целые положительные числа. 6. Предел целой положительной n -й степени корня фун- кции равен корню n -й положительной степени предела этой функции, т. е.
1)
2) (основание натуральных логарифмов).
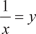 , а , а 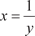 . Тогда согласно теореме 3.1 при х → у → 0 и второй замечательный предел принимает вид . Тогда согласно теореме 3.1 при х → у → 0 и второй замечательный предел принимает вид
. Кратко рассмотрим понятие непрерывности функции. Для этого напомним, что приращением функции y = f (x) в точке х 0 называется величина y = f (x) = f (x 0 + x) − f (x 0), где х есть приращение аргумента (рис. 3.30).
Рис. 3.30 Функция y = f (x) называется непрерывной в точке х 0, если она определена в какой-либо окрестности этой точки, и если выполняется следующее равенство
Докажем, например, что функция y = cos x непрерывна в любой точке х 0 своей области определения. Согласно определению непрерывности функции в точке х 0
получим
Пользуясь выражением для приращения функции, фор- мулу (3.4) можно переписать так:
Обозначим x 0 + x = x, тогда x будет стремиться к х 0 при x → 0, и окончательно получим
т. е. функция y = f (x) непрерывна в точке х 0, если она опреде- лена в некоторой окрестности этой точки и предел функции при стремлении аргумента к х 0 существует и равен значению функции в этой точке. Заметим, что функция является непрерывной на некото- ром интервале, если она непрерывна в каждой его точке. А все основные элементарные функции непрерывны на тех интерва- лах, в которых они определены. Приведем основные свойства непрерывных функций. 1. Алгебраическая сумма конечного числа непрерывных функций есть функция непрерывная. 2. Произведение конечного числа непрерывных функций есть функция непрерывная. 3. Частное двух непрерывных функций есть функция не- прерывная в тех точках, в которых делитель не равен нулю. 4. Если y = f (u) и u = (x) — непрерывные функции своих аргументов, то сложная функция y = f ((x)) также непрерывна. 5. Если функция y = f (x) непрерывна и имеет обратную функцию x = (y), то последняя также непрерывна. Если функция y = f (x) непрерывна, то в формуле (3.5) мож- но поменять местами знаки функции и предела, т. е.
Формула (3.6) означает, что если функция непрерывна, то для отыскания предела надо вместо аргумента х подставить предельное значение х 0. Это правило неприменимо в том слу- чае, когда при постановке предельного значения мы получаем неопределенности вида:
Теперь приведем конкретные примеры вычисления неко- торых пределов.
Пример 3.2.
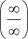 . Поэтому для решения подобных примеров ис- пользуют следующий прием: делят числитель и знаменатель на х в максимальной степени, в данном случае на х 5. Тогда получим: . Поэтому для решения подобных примеров ис- пользуют следующий прием: делят числитель и знаменатель на х в максимальной степени, в данном случае на х 5. Тогда получим:
Пример 3.5.
(Предел в квадратных скобках — это второй замечатель- ный предел).
Пример 3.7. Так как логарифмическая функция непрерывна, то можно воспользоваться формулой (3.5).
Данный предел можно свести к первому замечательному пределу путем замены переменной, т. е.
тогда получим: Пример 3.9.
Пример 3.11.
Пример 3.13.
Необходимо свести данный предел к первому замеча- тельному пределу. Для этого делаем замену переменной, т. е. arcsin x = y, x = sin y, при х → 0 у → 0.
Тогда получим: Комплексные числа Комплексным числом t называется выражение следующе- го вида: t = p + ig, p R, g R, где i — мнимая единица (i 2 = -1). В том случае, если р = 0 имеем чисто мнимое число t = ig. А если g = 0, то t = p, т. е. является действительным числом. Поэтому множество действительных чисел является подмно- жеством множества комплексных чисел (С), т. е. R C. Величина p есть действительная часть комплексного чис- ла t и обозначается p = Ret, а g — мнимая часть комплексного числа t и обозначается g = Imt. Комплексные числа t = p + ig и Пример 3.15. Комплексные числа t = 5 + 7 i; Два комплексных числа t 1 = p 1 + ig 1 и t 2 = p 2 + ig 2 будут равны только в том случае, когда равны их действительные и мнимые части, т. е. p 1 = p 2 и g 1 = g 2 Пример 3.16. Найти x и у из равенства 7 у + 4 хi = 18 − 9 i. Исходя из условия равенства комплексных чисел, получим 7y = 18 → y = 18/7; 4x = − 9 → x = − 9/4. Любое комплексное число t = p + ig можно изобразить точ- кой А (р, g) на плоскости 0 pg такой, что р = Rеt, g = Imt и, на- оборот, каждую точку А (p, g) координатной плоскости можно рассматривать как образ комплексного числа t (рис. 3.31). Плоскость 0 pg называется комплексной плоскостью, ось 0 р — действительной осью, а 0 g — мнимой осью.
. Угол, образованный этим радиусом-вектором с поло-
жительным направлением оси 0 р, называется аргументом = Arg t комплексного числа. Наименьшее по модулю значение Arg t называется его главным значением и обозначается аrg t. Заметим, что - < аrg t. Значение аргумента находят по формулам (см. рис. 3.31).
Алгебраической формой комплексного числа называется запись вида t = p + ig. А модуль Тогда получаем р = r cos; g = r sin; и, следовательно, комплексное число t = r (cos + i sin) можно записать в виде, который называется тригонометрической формой комплексно- го числа. Пример 3.17. Записать в тригонометрической форме комплексное число
Поэтому arg t = = /4.
Следовательно, получим Из формулы Эйлера cos + i sin = exp (i) следует пока- зательная форма комплексного числа: t = r exp (i), где r = |t|, а = arg t. Пример 3.18.
Найдем показательную форму комплексного числа.
Задачи для самостоятельного решения 1. Найти области определения функций: 1.1. 1.2. y = log5 (6 cos x − 2); 1.3. 1.4. y = 5 x 3 − 16 x 2 + 2 x − 7. 2. Найти пределы функций: 2.1. 2.4.
2.7.
2.8.
2.10.
2.11. 2.12. 3. Найти значение х и у из равенств: а) 17 x + 15 i = 2 − 8 iy; b) 6 x − (5 x − 3 y) i = 7 + 2 i; c) (16 − 3 i) x + (12 + 6) y = 10 + 6 i; d)(13 i − 10) x + (12 − 13 i) y = 12 − 23 i. 4. Записать комплексное число в тригонометрической и показательной формах. a) b) d) t = 6 i. 5. a)
b)
Вопросы для самопроверки 1. Что называется функцией одной независимой пере- менной? 2. Перечислить основные элементарные функции. 3. Какие функции называются элементарными? Приведи- те примеры. 4. Что такое предел функции y=f (x) при x → x 0? Дайте определение правого и левого пределов функции y = = f (x). 5. Дайте определение предела последовательности. 6. Какая функция называется бесконечно большой вели- чиной при x → x 0? 7. Какова связь между бесконечно большой и бесконечно малой величинами? 8. Сформулировать правила предельного перехода в слу- чае арифметических действий. 9. В чем состоит правило предельного перехода для непре- рывной функции? 10. Какое число называется комплексным? 11. Какие комплексные числа называются чисто мнимыми? 12. Какие комплексные числа называются сопряженными? 13. Что называется модулем и аргументом комплексного числа? 14. Как записываются комплексное число в тригонометри- ческой форме? 15. Как записываются комплексное число в показательной форме?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.177 (0.173 с.) |


 или
или 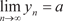 .
.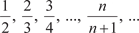 имеет предел, равный 1.
имеет предел, равный 1.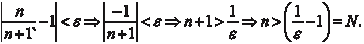
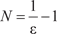
 . Данное нами определение иллюс-
. Данное нами определение иллюс-





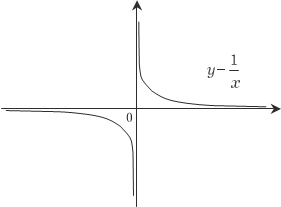
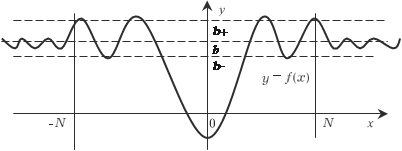
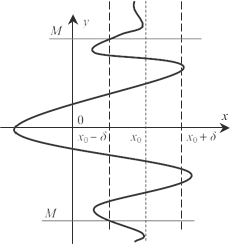 Рис. 3.28
Рис. 3.28

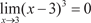 .
. — бесконечно большая величина и наоборот.
— бесконечно большая величина и наоборот.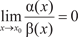
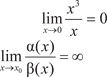 Если , то (x) есть бесконечно малая более вы- сокого порядка, чем (x).
Если , то (x) есть бесконечно малая более вы- сокого порядка, чем (x).
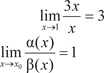 Если , где C R, то (x) и (x) — бесконечно малые одного порядка.
Если , где C R, то (x) и (x) — бесконечно малые одного порядка.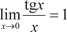





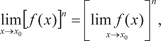

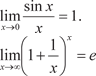 Приведем два замечательных предела, которые можно ис- пользовать при решении пределов.
Приведем два замечательных предела, которые можно ис- пользовать при решении пределов.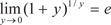
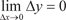 (3.4)
(3.4)


 , (3.5)
, (3.5)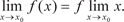

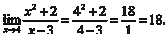

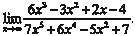
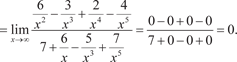
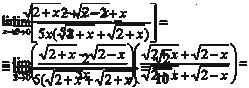
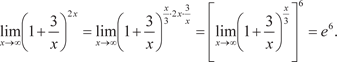
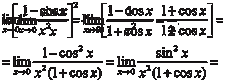
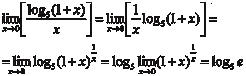

 при х → 0 у → 0,
при х → 0 у → 0,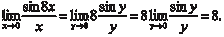
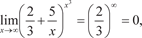 т. е. бесконечно малое.
т. е. бесконечно малое.
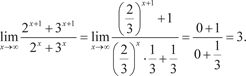
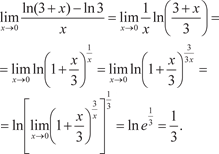

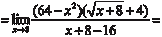
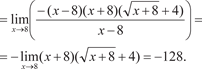
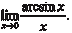
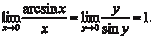
 = p − ig, отличающиеся только знаком мнимой части, называются комплексно сопря- женными.
= p − ig, отличающиеся только знаком мнимой части, называются комплексно сопря- женными.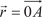

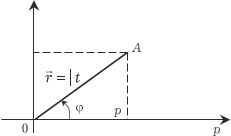
 Рис. 3.31
Рис. 3.31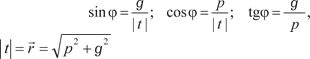 где — модуль комплексного числа t.
где — модуль комплексного числа t. и аргумент комплексного числа можно рассматривать как полярные координаты вектора
и аргумент комплексного числа можно рассматривать как полярные координаты вектора 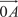 , изображающего комплексное число t (см. рис. 3.31).
, изображающего комплексное число t (см. рис. 3.31).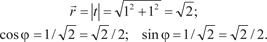 t = 1 + i.
t = 1 + i.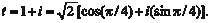


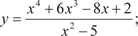
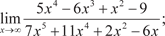 2.2.
2.2.  2.3.
2.3. 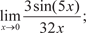


 2.6.
2.6.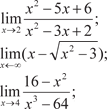 2.9.
2.9.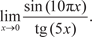
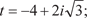
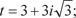 c) t = 2 − 2 i;
c) t = 2 − 2 i;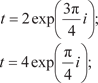 Записать комплексные числа в алгебраической и триго- нометрической формах.
Записать комплексные числа в алгебраической и триго- нометрической формах.