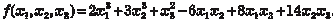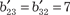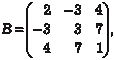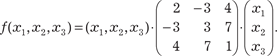Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные числа, собственные векторы матриц и квадратичные формы
Проблема собственных чисел играет существенную роль не только в линейной алгебре, но и в других разделах матема- тики, а также во многих прикладных областях (в менеджменте, психологии, юриспруденции).
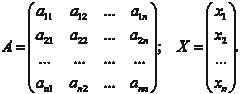
Пусть задана квадратная матрица А размера (n n), эле- ментами которой являются действительные числа (R) и вектор неизвестных Х размера (n 1): Предположим, что — это некоторое неизвестное дейс- твительное число. Если и ненулевой вектор Х удовлетворяют уравнению AX = X, (2.15) то называется собственным числом или собственным значе- нием матрицы А, а Х — собственным вектором этой же матри- цы, соответствующим. Преобразуем уравнение (2.15) к следующему виду: X − A X = 0, (E − A) X = 0, (2.16) где Е — единичная матрица.
Матрица называется характеристической матрицей. Так как по условию вектор неизвестных Х не равен нулю, то среди его координат x 1, x 2, …, x n должна быть хотя бы одна ненулевая. А для того, чтобы система линейных однородных уравнений (2.16) имела ненулевое решение, необходимо и до- статочно, чтобы определитель этой системы был равен нулю (это следует из теоремы Кронекера-Капелли).
(2.17)
Число = k, где Уравнение (2.17) называется характеристическим уравне- нием матрицы А и представляет собой алгебраическое уравне- ние степени n относительно:
Уравнение (2.18) имеет n корней 1, 2, …, n. Множество всех корней уравнения (2.18) называется спектром матрицы А. Заметим, что уравнение det (A − E) = 0 имеет те же корни, что и уравнение (2.17), т. е. det (A − E) = ( − 1)n det (E − A). Каждому собственному значению спектра матрицы А ста- вится в соответствие собственный вектор, определенный с точ- ностью до скалярного множителя. Если k есть кратный корень характеристического уравнения, то для произвольной квад- ратной матрицы число соответствующих собственных векто- ров может быть не равно кратности корня. С геометрической точки зрения собственный вектор определяет в пространстве некоторое направление (прямую, проходящую через начало координат), которое в результате преобразования не изменя- ется и вдоль которого пространство испытывает растяжение или сжатие в раз.
ческим полиномом. Коэффициенты p k можно вычис- лить по следующим рекуррентным формулам [57]:
щих на главной диагонали матрицы А). Заметим, что p n = (−1) n det A. При отыскании собственных чисел даже для матриц не- высокого порядка неизбежно большое количество вычислений. Для общего случая нельзя предложить оптимальный способ на- хождения собственных чисел и собственных векторов матрицы. Рассмотрим случай, когда собственные числа находятся сразу исходя из вида матрицы (исходная матрица либо диаго- нальная, либо верхняя или нижняя треугольная). В этом случае собственные числа 1, 2, …, n совпадают с элементами главной диагонали исходной матрицы a 11, a 22, …, a nn.
Пусть задана верхняя треугольная матрица А размера (n n): Тогда имеем
Отсюда видно, что собственные числа равны: 1 = a 11, 2 = a 22, …, n = a nn. С появлением ЭВМ получили распространение итераци- онные методы нахождения собственных чисел, которые не ис- пользуют вычисление характеристического полинома. К этим способам относятся: степенной метод, метод обратных итера- ций, QR -алгоритм, метод вращений Якоби, QL -алгоритм и др. Причем применение конкретного итерационного метода зави- сит от вида исходной матрицы А [4]. Теперь рассмотрим конкретные примеры.
Пример 2.8. Дана матрица А размера (3 3) Найти собственные числа и собственные векторы матри- цы А.
Из условия задачи видно, что матрица А является верхней треугольной матрицей. Поэтому собственными числами данной матрицы будут элементы ее главной диагонали Теперь найдем соответствующие найденным собственным числам собственные векторы. Для этого мы используем урав- нение (2.16). Для 1 = −4 получаем
где
Далее раскроем матричное уравнение (2.20)
В результате получим
Так как матрица этой системы вырождена, то она имеет ненулевые решения, которые имеют вид: т. е. получены искомые собственные вектора для 1 Для 2 = 3 = 1 получаем
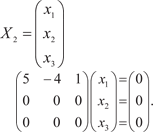 где где
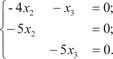
или в подробной записи
В результате получаем 5х 1 − 4х 2 − х 3 = 0 или х 3 = 5х 1 − 4х 2, т. е. это уравнение имеет ненулевые решения, которые и будут искомыми собственными векторами для 2.
Эти решения запишем в виде
Запишем характеристическое уравнение (2.17) для данно- го случая
Теперь найдем собственные векторы исходной матрицы А, соответствующие 1 = 1 и 2 = −4. Для 1 = 1 имеем
 . .
В подробной записи получим
Так как определитель полученной матрицы равен нулю, то она имеет ненулевые решения, которые и являются собствен- ными векторами Х 1, которые мы и находим Из первого уравнения системы получаем х 2 = 2 х 1. Из вто- рого уравнения системы получаем х 2 = 2 х 1, т. е. она имеет бес- конечное множество решений. И искомый собственный вектор Х 1 будет иметь вид
Аналогично, для 2 = −4 находим В заключение приведем два полезных правила [38]: 1)
сумма собственных чисел матрицы А равна следу этой матрицы, т. е. 2) произведение собственных чисел матрицы А равно оп- ределителю этой матрицы
Кратко рассмотрим квадратичные формы. Квадратичной формой называется однородный многочлен второй степени от нескольких пременных. Обозначим их х 1, х 2, … х n. Квадратичную форму в общем виде можно записать так:
В качестве примера рассмотрим квадратичную форму трех переменных: Введем обозначения:
Тогда квадратичная форма примет вид Дополнительно вводим симметричную матрицу В, век- тор
торный вид квадратичной формы.
где
где b ii − коэффициенты при Матрица В является матрицей квадратичной формы.
В качестве примера запишем в матрично-векторном виде квадратичную форму В данном случае получаем: b11 = 2; b22 = 3; b33 = 1; b12 + b21 = -6; b13 + b31 = 8; b23 + b32 =
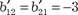 ; ; 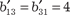 ; . ; .
Матрица данной квадратичной формы принимает вид А ее матрично-векторная запись такова:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.142.115 (0.027 с.) |

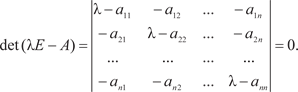
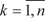 будет собственным числом только в том случае, если матрица (k E − A) — вырожденная.
будет собственным числом только в том случае, если матрица (k E − A) — вырожденная.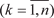
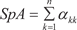
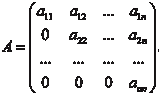
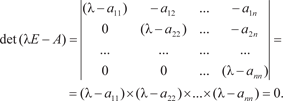
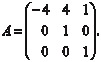
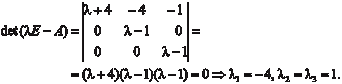
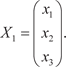
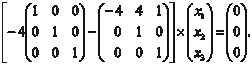
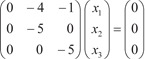
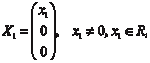
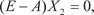
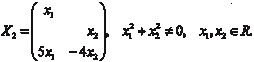
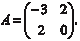

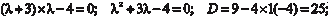
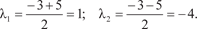
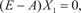
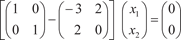 или
или 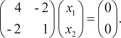
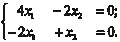
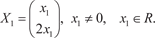
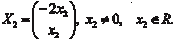
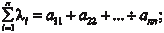
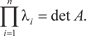
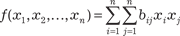
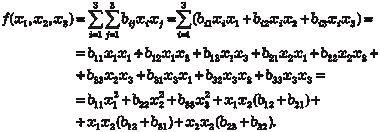
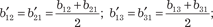
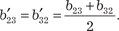
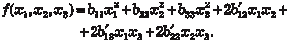
 .
.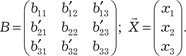
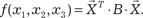
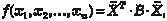
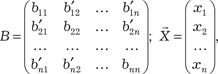
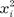 для всех i = 1, 2, …, n, а
для всех i = 1, 2, …, n, а 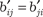 равны полусуммам коэффициентов при элементах, содержа- щих произведения x i x j и x j x i при всех i, j = 1, 2, …, n, i ≠ j.
равны полусуммам коэффициентов при элементах, содержа- щих произведения x i x j и x j x i при всех i, j = 1, 2, …, n, i ≠ j.