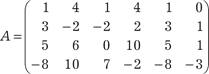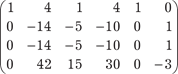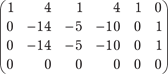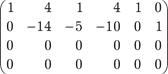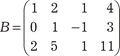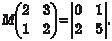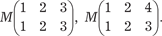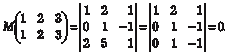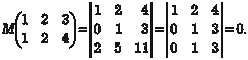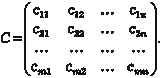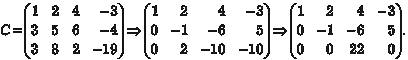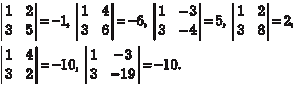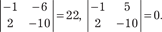Методы нахождения ранга матрицы

1. Метод элементарных преобразований

Элементарными преобразованиями являются следующие преобразования матрицы:

а) перестановка местами двух любых строк или столбцов матрицы;

б) умножение любой строки или столбца матрицы на не- равное нулю действительное число;

в) прибавление ко всем элементам какой-либо строки или столбца соответствующих элементов другой строки или столбца, умноженных на отличное от нуля действительное число.

Пример 2.3. Используя метод элементарных преобразова- ний, найдем ранг матрицы:

 

 

.

 

 

Первую строку домножаем последовательно на (-3); (-5); 8 и складываем со второй, третьей и четвертой строками. Тогда получаем:

 

 

.

 

 

Первую и вторую строки оставляем неизменными, третью строку умножаем на 3 и складываем с четвертой. После этого получаем:

 

.

Первую строку оставляем неизменной, а вторую строку умножаем на (-1) и складываем с третьей и получаем:

 

.

 

Ранг полученной матрицы равен двум, следовательно, и ранг исходной матрицы тоже равен двум, т. е. r (А) = 2. Заметим, что ранг матрицы не меняется при вычеркивании из нее нуле- вого столбца или строки.

2. Метод окаймления

Данный способ основан на следующей теореме.

Теорема 2.2. Предположим, что матрица А имеет отлич- ный от нуля минор порядка k и все ее миноры (k + 1)-го по- рядка, содержащие (окаймляющие) этот минор, равны нулю. В этом случае ранг матрицы А равен k.

Пример 2.4. Используя метод окаймления, найдем ранг матрицы

 

.

 

Выбираем в матрице В не равный нулю минор второго по- рядка, например минор

Он входит в состав следующих миноров:

Вычислим эти миноры:

Первую строку мы умножили на (-2) и сложили с третьей. Полученный определитель имеет две одинаковые строки и по пятому свойству определителей равен нулю.

Первую строку умножаем на (-2) и складываем с третьей, полученный определитель имеет две одинаковые строки и ра- вен нулю. Поэтому в соответствии с теоремой 2.2 ранг матрицы В равен двум, т. е. r (В)=2.

3. Метод прямоугольников

Пусть задана матрица

 

Предположим, что элемент С11 ≠ 0. Если это не так, то пере- ставляем строки местами. Элемент С11, строку и столбец, где он находится, назовем разрешающими. Алгоритм метода прямо- угольников состоит в следующем:

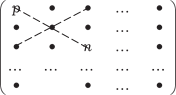
а) элементы разрешающей строки остаются неизменными; б) элементы разрешающего столбца, которые расположе-

ны ниже разрешающего элемента, пишем нулями;

в) все остальные элементы находим из вычисления опре- делителей второго порядка (их элементы и образуют прямо- угольник), в них разрешающий элемент вместе с пересчитыва- емым составляют главную диагональ (рис. 2.1).

Полученную в результате матрицу преобразуем по такому же алгоритму, взяв разрешающим элемент с ′22 ≠ 0. После этого алгоритм повторяется, а в качестве разрешающего элемента берется элемент с ″33 и т. д.

Процесс вычислений заканчивается, когда исходная мат-

рица приводится к верхней треугольной или верхней трапеци-

Рис. 2.1

евидной форме. А ее ранг будет равен числу ненулевых строк и одинаков с рангом исходной матрицы.

Пример 2.5. Используя метод прямоугольников, найти ранг следующей матрицы:

Поэтому ранг исходной матрицы С равен трем, т. е. r (С)=3.

На первом шаге разрешающим элементом будет 1, элемен- ты разрешающего столбца обнуляются, а остальные элементы матрицы находятся из вычисления определителей:

На втором шаге разрешающим элементом будет (-1), эле- менты разрешающего столбца обнуляются, а остальные эле- менты матрицы определяются с помощью вычисления следу- ющих определителей: