
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Основы дискретной математики
Основы теории множеств Начала теории множеств заложил в XIX в. немецкий ма- тематик Георг Кантор. Понятие множества является неопреде- ленным, внешним по отношению к математике, поэтому точно- го определения оно не имеет. Г. Кантору принадлежит высказывание, которое можно счи- тать интуитивным определением математики: “Множество есть многое, мыслимое как единое”. Это определение можно сформу- лировать несколько иначе. Множество — собрание различных объектов, которые различимы нашей интуицией. Данное опре- деление множества требует введения трех символов. Первый символ должен представлять само множество. В качестве него мы будем использовать заглавные буквы латинского алфавита А, В, С, … Второй символ — это элемент самого множества. Их мы будем обозначать маленькими буквами латинского алфави- та, т. е. a, b, c …. А третий символ должен однозначно сопоставить элемент самому множеству. В качестве этого символа применя- ют знак “∈”, который является первой буквой греческого слова εtri (быть). Следовательно, запись а ∈ А, говорит о том, что эле- мент а принадлежит множеству А, а запись b ∉ В, говорит о том, что элемент b не принадлежит множеству В. Заметим, что множества могут быть любой природы. Так можно говорить о множестве всех студентов МГУ, о множест- ве всех ядерных боеголовок РФ, о множестве всех спиральных галактик нашей Вселенной и т. д. Однако дальнейшее развитие теории множеств, которое опиралось на его интуитивное опре- деление, привело к ряду противоречий (парадоксов). Извест- ный логический парадокс Рассела мы приводим в этом пункте. А о семантическом парадоксе лжеца рассказано в подразд. 1.4. Заметим, что в логических парадоксах используют только понятия теории множеств, а в семантических парадоксах при- меняются такие понятия, как “характеризовать”, “истинный” и др., которые совсем не обязаны применяться в математиче- ском языке. Поэтому логические парадоксы представляют куда большую угрозу для математиков, чем семантические. Парадоксы теории множеств определились уже к началу XX в. Они показали, что построения, основанные на интуитив- ных определениях, не могут рассматриваться в математике как основополагающие. Поэтому надо определить множество так, чтобы затем при доказательствах теоретических построений не прибегать к интуитивным понятиям.
Выход из этой ситуации был найден в построении аксио- матической системы, которая бы опиралась на интуитивное оп- ределение множества, но затем не прибегала бы к нему в даль- нейших определениях и доказательствах теорем. К настоящему времени создано несколько аксиоматичес- ких систем теории множеств, которые в чем-то исключают, а в чем-то и дополняют друг друга. Одной из таких систем яв- ляется система Цермело (Z -система), которая состоит из семи аксиом, причем их нумерация не во всех источниках совпадает. Приведем формулировки этих аксиом по книге [5]. Z1. Аксиома объемности. Если все элементы множества Х принадлежат также мно- жеству Y, а все элементы множества Y принадлежат также множеству Х, то данные множества равны. Z2. Аксиома пары. Для произвольных х и y существует множество, единс- твенными элементами которого является х и у, т. е. { х; у }. Z3. Аксиома суммы. Для произвольных множеств X и Y существует единствен- ное множество Z, элементами которого являются все элементы множества X и все элементы множества Y и которое никаких других элементов не содержит. Z4. Аксиома степени. Для любого множества А существует множество всехего подмножеств 2А. Z5. Аксиома выделения. Путь А — произвольное множество, а ∈ А и F (a) — функ- ция со значениями на множестве {0, 1}. В этом случае сущест- вует множество С, для которого а ∈ C. Z6. Аксиома бесконечности. Существует по крайней мере одно бесконечное множест- во — натуральный ряд чисел. Z7. Аксиома выбора. Для семейства Х непустых непересекающихся множеств существует множество Y, имеющее только один общий элемент с каждым из множеств Р ∈ X. Следовательно, предполагается существование некоторой функции выбора ϕ, которая определяет получение единствен- ного общего элемента с каждым из множеств семейства Х. Аксиому Z7 некоторые математики разделяют, а другие не признают. Если все элементы множества Х являются также элемен- тами множества Y, то множество Х есть подмножество множест- ва Y. Это записывается следующим образом Х ⊂ Y или Y ⊃ Х.
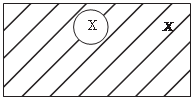
Множество всех подмножеств множества Y называется степенью этого множества и обозначается 2 y или Ρ(Y). Множество Х и Y являются равными (состоят из одних и тех же элементов) Х = Y, если Х ⊂ Y или Y ⊂ Х. Чтобы подчеркнуть тот факт, что рассматриваемое мно- жество Х может совпадать с множеством Y, записывают Х ⊆ Y. Вводится понятия пустого множества (∅), которое не со- держит ни одного элемента. Например, множество решений уравнения х 2 + 4 = 0 есть пустое множество. Способы задания множеств а) Словесное описание. Например, множество Х есть множество всех прямых, про- ходящих через точку А плоскости. б) Перечисление элементов, входящих в множество. Например, Х = {-7, 0, 12, 123, 700}. Элементы в приведенном списке могут располагаться в любом порядке и должны быть различны, т. е. множества Х = {5, 5, 7} и Y = {5, 7} равны между собой. Если во множестве есть совпадающие элементы, то его называют семейством Z = (5, 9, 9, 12, 12, 23) и заключают в круг- лые скобки. в) Описание свойств элементов, входящих в множество. Х = { x | [(х − 3)(х − 5)] > 0}, т. е. элементами множества Х будут только те числа, которые удовлетворяют неравенству (х − 3)(х − 5) > 0. Если обозначить через Q(х) свойства элементов, входящих во множество Х, то для задания этого множества в общем слу- чае можно использовать следующую запись Х = { х | Q (х)}, т. е. множество Х состоит из тех элементов х, которые удовлетворя- ют свойству Q (х). Множество, которое содержит все рассмат- риваемые в некоторой задаче множества, называется универ- сальным и обозначается U. Например, в качестве U можно взять множество N (заме- тим, что в некоторых монографиях оно начинается не с едини- цы, а с нуля). Z = {z N | z < 6}, т. е. Z = {1, 2, 3, 4, 5}. Для сокращения записи в математике используют кванто- ры всеобщности, существования, существования и единствен- ности: — квантор всеобщности (перевернутая первая буква ан- глийского слова All); — квантор существования (перевернутая первая буква английского слова Exists); ! — квантор существования и единственности. Например, запись (х Х) Р(х) означает: для всех х измножества Х справедливо Р(х); запись (у Y) R(у) — сущес- твует у из множества Y такое, что справедливо R(у); запись (! z Z) М(z) — существует единственное z из множества Z такое, что справедливо M(z). Операции над множествами Пусть задано универсальное множество U. Множество всех его подмножеств есть 2 U. Заданы также множества Х и Y, причем Х 2 U и У 2 U. Дополнением множества Х называется множество Х эле- ментов множества U, которые не принадлежат Х: Х = {х U | х Х}. Графически операции над множествами (рис. 1.1) можно изображать с помощью кругов Эйлера (диаграмм Венна): U
Х — круг; Х — заштрихованная область прямоугольника.
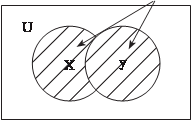
Рис. 1.1 Пересечение (X Y) двух множеств Х и Y состоит из эле- ментов, принадлежащих обоим этим множествам (рис. 1.2). Объединение (Х Y) двух множеств Х и Y состоит из эле- ментов, которые принадлежат хотя бы одному из множеств Х и У (рис. 1.3). X Y={x | x X и x Y} Х Y X Y={x | x X или x Y} Х Y
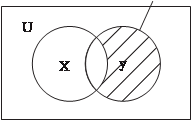
Рис. 1.2 Рис. 1.3 Разность (Х \ Y) двух множеств Х и Y состоит из элементов, принадлежащих X, но не принадлежащих Y (рис. 1.4). Аналогично определяется разность (Y \ Х) множеств Y и Х
(рис. 1.5). X \ Y = { x | x X и x Y } Х \ Y Y\X = {y | y Y и y X}
Рис. 1.4 Рис. 1.5 Симметрическая разность (Х У) множеств Х и Y состоит из элементов, которые принадлежат ровно одному из множеств Х и Y (рис. 1.6): X Y=(X\Y) (Y\X)=(X Y)\(X Y) Х Y
Теперь рассмотрим конкретный числовой Пример 1.0. Дано множество: Х = {-5, 0, 3, 17, 28, 33, 100}. Y = {-7, 0, 5, 17, 33, 108}. Х Y = {0, 17, 33}. Х Y = {-7, -5, 0, 3, 5, 17, 28, 33, 100, 108}. Х \ Y = {-5, 3, 28, 100}. Y \ Х = {-7, 5, 108}. Х Y = {-7, -5, 3, 5, 28, 100, 108}. Мощность множеств Число элементов в конечном множестве Х называютего мощностью и обозначают | X | или # Х. Например, X = {5, 12, 23, 111}, | X | = 4. Если известны мощности множеств Х и Y, то можно найти мощность их объединения по формуле: |X Y| = |X| + |Y| − |X Y|. В общем случае имеем:
Для подсчета элементов в конечных множествах можно использовать комбинаторику. Если между двумя множествами можно установить взаим- но однозначное соответствие, то в них одинаковое количество элементов. Взаимная однозначность показывает, что каждому эле- менту первого множества соответствует один элемент второго и наоборот. Рассмотрим пример осуществления этого принципа. Каких подмножеств больше у 100-элементного множества: мощности 60 или мощности 40. Используем понятие числа сочетаний из n элементов по k (они отличаются только составом элементов) (более подробно в подразд. 1.2). Число сочетаний находится по формуле
где n! = 1 2 3 … n (читается n факториал). В нашем случае имеем:
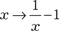
Поэтому у 100-элементного множества одинаковое коли- чество подмножеств мощности 60 и 40 элементов. Два множества называются равномощными, если между ними можно установить взаимно однозначное соответствие. Для конечных множеств это означает, что в них одинако- вое количество элементов. Но это определение годится и для бесконечных множеств. Например, отрезки [0,1] и [0,10] равномощны, так как отобра- жение х 10 х дает нужное соответствие. Можно также доказать, что интервал (0,1) и луч (0, + ) равномощны. Искомое взаимно однозначное соответствие име- ет вид Так же доказывается, что множество бесконечных после- довательностей цифр 0, 1, 2, 3 равномощно множеству беско- нечных последовательностей цифр 0 и 1. Тот факт, что множество Х равномощно (эквивалентно) множеству Y записывается так: X ~ Y (| X | = | Y |). Множество называется счетным, если оно равномощно множеству натуральных чисел (N).
Например, множество целых чисел (Z) равномощно N, т. е. Z~N. Доказывается: 1) подмножество счетного множества конечно или счетно; 2) всякое бесконечное множество содержит счетное под- множество; 3) объединение конечного или счетного числа конечных или счетных множеств конечно или счетно. Множество действительных чисел (R) или множество бес- конечных последовательностей 0 и 1 несчетно. Мощность мно- жества R больше мощности любого счетного множества и назы- вается мощностью континуума. Приведем без доказательства теорему Кантора—Берн- штейна. Если множество Х равномощно какому-то подмножеству множества Y, а множество Y равномощно какому-то подмно- жеству множества Х, то множества Х и Y равномощны. Дадим также общую формулировку теоремы Кантора. Никакое множество Z не равномощно множеству всех сво- их подмножеств. Наглядные представления о множествах могут приводить к противоречиям. Приведем, например, парадокс Рассела. Типичные множества не являются своими элементами. Например, множество целых чисел (Z) само не является це- лым числом и не будет своим элементом. Но в принципе можно представить себе множество, которое является своим элемен- том, например, множество всех множеств (U). Такие множест- ва назовем “необычными”. Теперь рассмотрим множество всех обычных множеств. Если оно обычное, то является своим эле- ментом и, следовательно, оно — необычное, и наоборот. В принципе понятие “множество” не является непосредс- твенно очевидным: разные люди (научные школы) могут пони- мать его по-разному.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.05 с.) |
 U — изображается прямо- угольником;
U — изображается прямо- угольником;

 Y \ Х
Y \ Х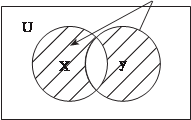 Рис. 1.6
Рис. 1.6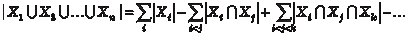
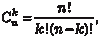
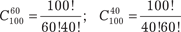
 .
.


