
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции, прямые произведения, отношения
Сначала дадим традиционное определение функции. Даны два множества Х и Y. Функцией, которая определена на множестве Х и принимает значение на множестве Y, называ- ется закон (f), по которому каждому элементу х из множества Х (х Х) ставится в соответствие один элемент у из множест- ва Y (у Y). Обычно это записывают в виде у = f (х). Множес- тво Х есть область определения функции f, а множество Е = = { у Y | ∃ х Х у = f (х)} Y — множеством значений функ- ции f. Функцию f, определенную на множестве Х и принимаю- щую значения на множестве Y, обозначают так f: Х Y. Элемент х Х называется независимой переменной (аргу- ментом), элемент f (х) называется значением функции на эле- менте х. Пусть задана однозначная функция f, т. е. различным значениям ее аргументов соответствуют различные значения функции (х 1 Х) (х 2 Х) (х 1 х 2) ⇔ (f (х 1) f (х 2)). Знак “⇔” означает эквивалентность, например А ⇔ В значит, что А экви- валентно В. (А тогда и только тогда, когда В). Тогда у Е может быть поставлен в соответствие един- ственный элемент х Х, такой что у = f (х) и который обозна- чается х = f -1(у). Это значит, что на множестве Е определена функция f -1(у), которая принимает значения на множестве Х и называется обратной к функции f. Если задана функция f -1 (у): Е Х и Y = Е, т. е. когда множество значений функции f со- впадает со всем множеством Y, функцию f называют взаимно однозначным соответствием между множествами Х и Y. Теперь сформулируем определение прямого или декарто- ва произведения. Прямым произведением множеств Х 1, Х 2, Х 3, …, Х n, n 2 называется множество различных упорядоченных наборов (n -мерных векторов) (х 1, х 2, х 3, …, х n), где х 1 Х 1, х 2 Х 2, х 3 Х 3 …, х n Х n, обозначаемое Х 1 Х 2 Х 3 … Х n = х n) | х 1 Х 1, х 2 Х 2, …, х n Х n }={(х 1, х 2, …, х n) | х i Х i,
В частном случае, если имеется два множества Х и Y, их прямым произведением будет множество различных упорядо- ченных наборов (двумерных векторов) (х, у), где х Х, а у Y, обозначаемые Х Y = {(х, у) | х Х, у Y }. Например, имеем два множества Х ={5, 6}, Y ={ln3, ln7}. Х Y = {(5, ln3), (5, ln7), (6, ln3), (6, ln7)}. Y Х = {(ln3, 5), (ln7, 5), (ln3, 6), (ln7, 6)}.
т. е. Х Y Y Х. Теперь дадим определение отношения. Даны множества Х 1, Х 2, …, Х n, n 1; n -местным отношением между элементами множеств Х 1, Х 2, …, Х n называется любое подмножество пря- мого произведения этих множеств, т. е. Х 1 Х 2 , …, Х n. Если (х 1, х 2, …, х n) говорят, что элементы х 1, х 2, …, х n связа- ны отношением.
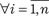 , Хn, говорят, что есть n -местное , Хn, говорят, что есть n -местное
отношение на множестве Х. Для одноместных, двухместных и трехместных отношений часто используют специальные названия: унарные, бинарные, тернарные соответственно, т. е. n = 1 — унарное отношение Х 1; n = 2 — бинарное отношение Х 1 Х 2; n = 3 — тернарное отношение Х 1 Х 2 Х 3. Если отношение совпадает с прямым произведением, оно называется полным, т. е. = Х 1 Х 2 … Х n. Рассмотрим конкретные примеры отношений. Пример 1.1. X = {1, 2, 7, 23, 35, 56}, = { х | х Х и х < 23}, = {1, 2, 7}, т. е. при n = 1 отношение есть подмножество множества Х. Пример 1.2. Х 1 = {0, 1, 2}; Х 2 = {5, 6, 7}; = {(х 1, х 2) | х 1 Х 1, х 2 Х 2, х 2 < 6}; = {(0, 5), (1, 5), (2, 5)}. Особый интерес представляют бинарные отношения, кото- рые мы рассмотрим более подробно. Если есть отношение между элементами множеств Х и Y, т. е. Х Y, можно использовать запись х у, т. е. x связано с y соотношением. Обратным к отношению Х Y называется отношение -1 ={(у,х)|(х,у) } Y Х.
Геометрически понятие бинарного отношения показано на рис. 1.7. Рис 1.7 D ={ х | х Х, (ху) } — множество определения отноше- ния Х Y Е ={ у | у Y, (ху) } — множество значений отношений Х Y.
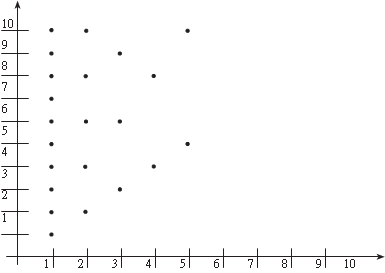
Точка х — элемент множества D, а множество (х) есть -образ элемента х, а точка у является некоторым элементом из (х). Отсюда видно, что бинарное отношение является много- значной функцией. Заметим, что прямое произведение множества действи- тельных чисел (R) само на себя R R = R 2 представляет собой систему координат на плоскости х 0 у. Отношение Х Y R 2 является графиком отноше- ния. Теперь рассмотрим конкретный пример бинарного отно- шения. Пример 1.3. Дано множество Х = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Найдем отно- шение, если оно задано так: = {(х 1, х 2) | х 1 Х, х 2 Х, х 1 — делитель х 2, х 1 5 }. Отношение имеет вид.
= {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8), (1,9), (1,10), (2,2), (2,4), (2,6), (2,8), (2,10), (3,3), (3,6), (3,9), (4,4), (4,8), (5,5), (5,10)}. Теперь найдем множество определения и множество зна- чений отношения: D = {1, 2, 3, 4, 5}, Е = Х. Представим полученное отношение в графическом виде. Для этого зададим систему координат. Осью абсцисс будет D, а осью ординат Е. По этим осям отложим элементы исходного множества Х, затем соответствующие пары (х 1 х 2) отметим точ- ками и получим графическое изображение нашего отношения (рис. 1.8). Бинарные отношения можно представить в виде графа (множества вершин и множества ребер, см. раздел “Основы те- ории графов”). Вершинами будут элементы исходного множества Х, а реб- рами пары (х 1 х 2). В данном случае важен порядок следования эле-
D
Рис. 1.8 ментов, поэтому ребра будут ориентированными (обозначим их стрелками). В результате получим следующий граф (рис. 1.9).
Рис. 1.9 В случае х 1 = х 2 получим петлю. Наконец бинарное отношение можно представить в виде матрицы, т. е. прямоугольной таблицы размера n m, где n — количество строк, а m — количество столбцов. Например, если имеем два множества Х = { х 1, х 2, …, х n}, Y = { у 1, у 2, …, у m} и бинар- ное отношение на элементах этих множеств Х Y = = {(ху) | х Х, у Y }, то этому отношению соответствует матрица размера n m, состоящая из нулей и единиц. Единицами обозначаются пары (ху), входящие в отношение. (Более подробно о матрицах см. в главе 2 “Элементы линейной и векторной алгебры”.) В данном примере имеем отношение Х 2, т. е. ему соот- ветствует матрица размера 10 10, число строк и столбцов ко- торой равно числу элементов в множестве Х (рис. 1.10).
Рис. 1.10 В заключение рассмотрим функцию как отношение. Отношение f между элементами множеств Х и Y называ- ется функцией, определенной на множестве Х и принимающей значение на множестве Y, если х Х ∃! у У | (х,у) f. (1.1) В этом случае пишут f: Х У, а вместо (х,у) f обычно пи- шется у = f (х); у называют значением функции f на элементе х, так как для функциональных отношений в силу (1.1) f -образом одноэлементного множества { х } будет одноэлементное множес- тво { f (х)}. Заметим, что (1.1) эквивалентно выполнению двух условий: f -1(У) = Х; (1.2) у 1 = f(х) и у 2 = f(х) ⇒ у 1 = у 2. (1.3) Иногда отношения называют функцией, если выполнено только условие (1.3), а если выполнено и условие (1.2), то отоб- ражением. Часто слова функция и отображения используют как си- нонимы.
Основные понятия комбинаторики Комбинаторика — часть математики, которая посвящена решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными правилами, т. е. комбинаторика решает задачи выбора элементов из конеч- ного множества и размещения этих элементов в каком-либо по- рядке. Приведем правила сложения и умножения, которые при- меняются в комбинаторике.
Правило сложения. Если выбор каждого из объектов А i ( Правило умножения. Если выбор каждого из k объектов В i ( Приведем конкретные примеры применения этих правил. Пример 1.4. Из Москвы в Санкт-Петербург можно добрать- ся самолетом, поездом, автобусом. Есть пять автобусных мар- шрутов, два авиамаршрута, один железнодорожный. Поэтому общее число маршрутов между Москвой и Санкт-Петербургом равно: n = 5 + 2 + 1 = 8. Пример 1.5. Из пункта А в пункт В можно доехать по 5 до- рогам, из В в С — по трем дорогам, а из С в D — по четырем дорогам (рис. 1.11). Сколькими способами можно проехать из А в D через В и С?
Рис. 1.11 По правилу произведения получаем N = 5 · 3 · 4 = 60.
Размещения Дано множество, состоящее из n элементов. Размещением из n элементов по m элементам (0 m n) называется любое упорядоченное подмножество, содержащее m различных эле- ментов исходного множества. Все эти подмножества отлича- ются друг от друга или составом элементов, или порядком их распределения.
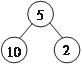
Обозначим размещения из n элементов по m где n! = 1 2 3 … n (читается n факториал). Принимается, что 0! = 1 и Пример 1.6. В футбольной премьер-лиге РФ участвует 16 команд. Сколькими способами можно распределить три пер- вых призовых места?
Число размещений по m элементов с повторениями из n элементов равно nm, т. е.
Пример 1.7. Сколько трехзначных чисел можно составить из цифр 5,6,7,8. трехзначных числа. Перестановки
Перестановкой из n элементов называется размещение из n элементов по n элементов. Так как каждая перестановка содержит все n элементов исходного множества, то различные перестановки отличаются друг от друга только порядком сле- дования элементов, т. е. Пример 1.8. Расставить четыре книги на полки можно P 4 = = 1 2 3 4 = 24 способами.
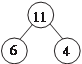
Если среди n элементов есть n 1 элементов одного вида, n 2 элементов другого вида, …, n i элементов i -го вида, то число пе- рестановок с повторениями находится по формуле Пример 1.9. Сколько различных шестизначных чисел мож- но записать с помощью цифр: 2, 2, 3, 3, 4, 4. В данном случае n = 6, n 1 = 2, n 2 = 2, n 3 = 2, т. е.
Сочетания Дано множество, состоящее из n элементов. Сочетанием из n элементов по m элементам (0 m n) называется любое подмножество, которое содержит m различных элементов ис- ходного множества. Различными подмножествами считаются только те, которые отличаются по составу элементов.
Обозначив число сочетаний через  , получим , получим
Пример 1.10. В бригаде 25 человек. Надо найти четырех человек для работы в ночную смену. Сколькими способами это можно сделать.
Так как порядок выбранных четырех рабочих не имеет значения, то имеем Число сочетаний с повторениями из n элементов по m на- ходятся по формуле
Пример 1.11. Число различных бросаний трех одинаковых кубиков равно
С числами  связано функциональное тождество, которое называется формулой бинома Ньютона. Для любых n ∈ N верно равенство связано функциональное тождество, которое называется формулой бинома Ньютона. Для любых n ∈ N верно равенство
При а = 1 имеем
Пример 1.12. Используя бином Ньютона найти (1 + b)7.
Основы теории графов Впервые термин “граф” был употреблен венгерским ма- тематиком Д. Кенигом в 1936 г. Но начало теории графов было положено Л. Эйлером в 1736 г., когда он решил задачу о ке- нигсбергских мостах и нашел критерий существования в гра- фе специального маршрута (эйлерова цикла). Но как матема- тическая дисциплина теория графов сформировалась именно в первой трети ХХ в. Эта теория располагает аппаратом ре- шения различных прикладных задач из разных областей на- уки и техники, например, сетевое планирование и управление. В настоящее время теория графов — один из наиболее быстро развивающихся разделов математики. Предположим, что V — это непустое конечное множество, а V (2) — это множество всех его двухэлементных подмножеств. Множество Е является произвольным подмножеством множес- тва V (2), т. е. E V (2). Тогда графом (G) называется пара множеств (V, E), т. е. G = (V, E), где VG — множество вершин графа, а EG — множе- ство его ребер. Любое ребро графа определяется парой его вер- шин. Если все пары вершин упорядоченные, то граф называется ориентированным (его ребра обозначают стрелками), в против- ном случае он — неориентированный. В том случае, если в гра- фе есть ориентированные и неориентированные ребра, он на- зывается смешанным. Ориентированный граф G можно задать как отношение, т. е. как подмножество прямого произведения множества его вершин V само на себя. G V V. В этом случае множество всех двухэлементных подмно- жеств V(2) заменяется декартовым произведением V V. Графы обычно изображаются в виде рисунков, на которых вершины изображаются кружками (точками), а ребра отрезка- ми (рис. 1.12).
а) неориентирован- ный граф б) ориентированный граф Рис. 1.12 в) смешанный граф Приведем конкретный пример. Пример 1.13. Пусть задано множество V ={1,2,3}. Тогда V(2) = {(1,2), (1,3), (2,3), (1,1), (2,2), (3,3), (2,1), (3,1), (3,2)}.
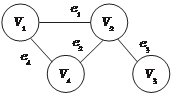
Предположив, что порядок вершин имеет значение, получаем следующий ори- ентированный граф (рис. 1.13). Далее вершины графа будем обозна- чать буквами V 1, V 2, V 3, …, V n, а ребра e 1, e 2, …, e m. Вообще говоря, две вершины V i и V j
В этом случае ребро становится петлей (рис. 1.15). Граф, имеющий петли, иногда называют псевдографом (рис. 1.16) Рис. 1.13
Рис. 1.14 Рис. 1.15
Рис. 1.16 Между двумя вершинами может проходить и несколько ребер (ориентированных и неориентированных), их называ- ют параллельными. А граф, имеющий такие ребра, называют мультиграфом (см. рис. 1.17). Мультиграф — это пара (V, E),
где V — множество вершин, а Е — семейство подмножеств множества V (2). Употребление термина “семейство” говорит о том, что элементы множества V (2) могут повторяться (возмож- ны параллельные ребра).
Граф G называется графом порядка n, если он содержит n вер- шин. (На рис. 1.18 приведен граф восьмого порядка.)
Рис. 1.18
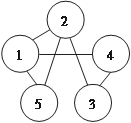
Граф, который не имеет ребер (состоит только из вершин) называется пустым (рис. 1.19). Рис. 1.19 Граф, не имеющий вершин, называется ноль-графом (). Две вершины называются смежными, если они являются кон- цевыми вершинами какого-то ребра (например, вершины V 1 и V 3; V 2 и V 7 на рис. 1.18).
e; e и e на рис. 1.20). 2 2 4 Если имеют в виду разные эле- менты графа (вершины и ребра), то используют понятия инцидентнос- Рис. 1.20 ти, т. е. ребро инцидентно своим концевым вершинам (напри- мер, ребро e3 инцидентно вершинам V 2 и V 3). Число инцидентных вершине ребер называется степенью (валентностью) этой вершины и обозначается d (V i). Например, степень вершины V 2 равна 3 (d (V 2) = 3). Вершина степени 1 называется висячей, вершина степени ноль — изолированной, а петля при вершине добавляет в сте- пень этой вершины двойку. Например, вершина V 4 на рис. 1.21 является висячей, а вер- шина V 6 — изолированной, а степень вершины V 1 равна 4 (dV 1 = = 4, два ребра и петля). Граф называют полным, если две любые его вершины смежные (см. рис. 1.13). Приведем без доказательства две теоремы. Теорема 1.1. Сумма степеней вершин графа равна удвоен- ному числу его ребер. У графа на рис. 1.21 имеется 7 ребер,а сумма степени его вершин равна — 14. Теорема 1.2. Число вершин нечетной степени в любом гра- фе четно. Например, у графа, изображенного на рис. 1.21 таких вершин две (V 4 и V 5).
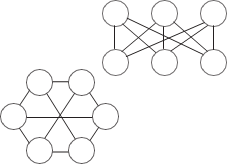
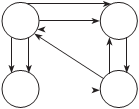
Рис. 1.21 Может оказаться, что один и тот же граф изображается разными рисунками. Говорят, что два графа G 1 и G 2 изоморф- ны, если существует такое взаимнооднозначное соответствие между множествами их вершин и ребер, что соответствующие ребра графов ицидентны соответствующим вершинам этих графов. Если ребра ориентированы, то их направления также должны соответствовать друг другу. На рис. 1.22 приведен пример изоморфных графов.
Рис. 1.23 Рис. 1.22
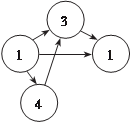
Маршруты, цепи, пути, циклы Маршрут в графе — это конечная чередующаяся последо- вательность вершин и ребер, начинающаяся и оканчивающая- ся на вершине, причем одинаковые вершины и ребра в марш- руте могут повторяться. Например, маршрут V 1 e 1 V 2 e 5 V 4 e 6 V 1 e 8 V 6 e 7 V 4 на рис. 1.24. Маршрут называют открытым, если его конечные верши- ны различны, в противном случае он является замкнутым, на- пример маршрут V 1 e 1 V 2 e 5 V 4 e 6 V 1 e 8 V 6 e 7 V 4 e 6 V 1 на рис. 1.24.
Рис. 1.24 Маршрут называют цепью, если все его ребра различны. Цепь является открытой, если ее конечные вершины различ- ны, в противном случае она — замкнутая. На рис. 1.25 V 2 e 1 V 3 e 3 V 5 e 13 V 1 e 5 V 3 e 8 V 4 — открытая цепь, а V 1 e 13 V 5 e 3 V 3 e 2 V 2 e 1 V 3 e 7 V 1 — замкнутая цепь. Открытую цепь называют путем, если все ее вершины раз- личны, например V 4 e 8 V 3 e 6 V 1 e 11 V 6 на рис. 1.25. Замкнутую цепь называют циклом, если все ее вершины за исключением концевых различны, например V 3 e 3 V 5 e 13 V 1 e 7 V 3 на рис. 1.25.
Рис. 1.25 Две несовпадающие вершины V i и V j в графе G называются связными, если существует маршрут V i - V j. Граф G называют связным, если две его любые несовпада- ющие вершины могут быть соединены маршрутом. Например,
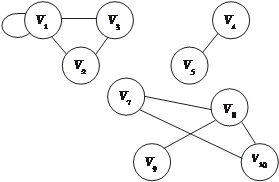
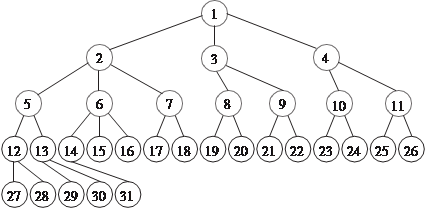
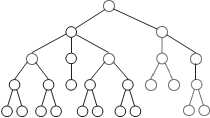
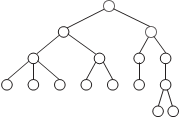
связными являются графы на рис. 1.24 и 1.25, а несвязным — граф, изображенный на рис. 1.26. Рис. 1.26 Деревья и лес Большую роль в различных отраслях науки имеют связные ациклические (не имеющие циклов) графы, мощность множества ребер которых на единицу меньше мощности множества вершин, т. е. если | VG | = m, то | EG | = m − 1. Эти графы носят название дере- вьев. Заметим, что (m − 1) — это минимальное количество ребер для того, чтобы граф был связным. Примерами древовидной структуры являются генеалоги- ческий граф, схема вертикали управления любой организации, совокупность всех файлов, размещенных на диске ПЭВМ. При- мер дерева приведен на рис. 1.27. Несвязный граф, компонентами которого являются дере- вья, называется лесом (рис. 1.28).
Матрицы графов 1. Матрица инцидентности. Рассмотрим простой граф G (без петель и параллельных ребер), имеющий n вершин и m ребер. Ему соответствует мат- рица инцидентности размера n m, т. е.
Рис. 1.27
Рис. 1.28 А I = [a ij ], где Каждый элемент этой матрицы a ij в случае ориентирован- ного графа определяется следующим образом.
если ребро j инцидентно вершине i и входит в нее; если ребро j неинцидентно вершине i.
если ребро j неинцидентно вершине i.
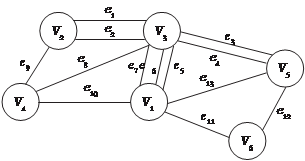
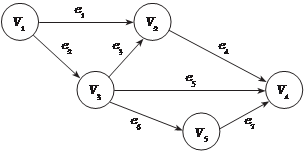
Рассмотрим конкретный пример. Имеем ориентированный граф, имеющий 5 вершин и 7 ребер. (рис. 1.29). Рис. 1.29 Ему соответствует матрица инцидентности размера 5 7 следующего вида
V e 2 В случае задания мультиграфа V (имеет параллельные ребра) матрица 1 2 e 3 инцидентности определяется по при- e 5 e 4 e 7 e 8
веденным выше правилам. Например,
3 4
Рис. 1.30 найдем матрицу инцидентности для графа, изображенного на рис. 1.30. Искомая матрица имеет размер (4 9) и выглядит следующим образом
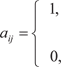
2. Матрица смежности. Пусть задан псевдограф (имеет петли), содержащий n вер- шин и m ребер. Матрицей смежности этого графа A s называется матрица размера n n, т. е. A s = (a ij), Любой элемент этой матрицы a ij в случае ориентированно- го графа определяется следующим образом.
в противоположном случае. В случае, если граф G неориентированный, то любой эле- мент его матрицы смежности определяется так:
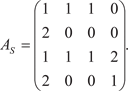
для графа, изображенного на рис. 1.31. Рис. 1.31 Искомая матрица смежности имеет размер 4 4 и выгля- дит так:
В том случае, если граф кроме петель имеет параллельные ребра, матрица A s находится по следующим правилам. Если задан ориентированный граф, то каждый элемент его матрицы смежности находится так:
в противоположном случае. В случае неориентированного графа имеем:
V j; в противоположном случае.
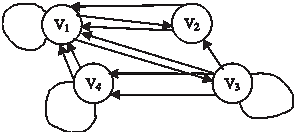
Найдем матрицу смежности для графа, изображенного на рис 1.32.
Рис. 1.32 Данному графу соответствует матрица смежности разме- ра 4 4, имеющая вид:
Раскраски Задачи раскраски вершин или ребер графа занимают важ- ное место в теории графов. Особенностью этих задач является существование объектов, которые по каким-то причинам могут быть объединены в одну группу. Пусть G = (V, Е) — граф, k N. Произвольная функция вида f: VG {1, 2, 3, …, k } называется вершинной k -раскраской, или просто k -раскраской. Раскраска называется правильной, если для любых смежных вершин V i и V j выполняется нера- венство f (V i) f (V j). Граф, для которого существует правильная k -раскраска называется k -раскрашиваемым. В определении раскраски вместо множества {1, 2, 3, …, k } можно взять произ- вольное k -элементное множество. Правильную k -раскраску графа можно трактовать как окрашивание каждой его вер- шины в один из k цветов, при этом смежные вершины должны быть окрашены в разные цвета. При k -раскраске может быть использовано и менее k цветов. Правильную k -раскраску гра- фа G можно рассматривать как разбиение V 1 V 2 … V t = VG, t k множества вершин VG на не более чем k непустых классов, каж- дый из которых является независимым множеством. Классы этого разбиения называются цветными классами. Минималь- ное число k, при котором граф G является k -раскрашиваемым, называется хроматическим числом этого графа и обозначается χ(G). Если χ(G) = k, то граф G называется k -хроматическим. Пра- вильная k -раскраска G при k = χ(G) называется минимальной. На рис. 1.33 приведена одна из правильных 4-раскрасок, причем меньшим числом цветов этот граф раскрасить нельзя (краски обозначены номерами).
Рис. 1.33 Плоские и планарные графы В некоторых случаях необходимо знать, можно ли изобра- зить граф на плоскости так, чтобы его изображение удовлетво- ряло некоторым условиям. Например, в радиоэлектронике при изготовлении микросхем проводники электрического тока не должны пересекаться. Такая же задача возникает при проек- тировании железнодорожных трасс, когда нежелательны пе- реезды. Поэтому вводится понятие плоского графа. Плоским называют граф, вершины которого являются точ- ками плоскости, а ребра — непрерывными плоскими линиями без самопересечений, соединяющими соответствующие вер- шины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины. Примеры плоских графов показаны на рис. 1.34.
Рис. 1.34 Любой граф, изоморфный плоскому графу, называется пла- нарным. На рис. 1.35, а приведен плоский граф, а на рис. 1.35, б — планарный граф, изоморфный графу на рис. 1.35, а.
б)
Проблема раскраски планарных графов является одной из самых знаменитых в этой теории. Первоначально вопрос формулировался так: достаточно ли четырех красок для такой раскраски произвольной географической карты, при которой любые две соседние страны окрашены в разные цвета. Рас- сматриваются только те карты, в которых граница любой стра- ны состоит из одной замкнутой линии, а соседними считаются страны, имеющие общую границу ненулевой длины. Позднее понятие карты сформулировали так: карта — это связный плоский мультиграф без мостов (ребро графа называ- ется мостом, если его удаление увеличивает число компонент графа, мостами являются ребра e и t в графах на рис. 1.35, а, б). В 1879 г. английский математик А. Кэли сформулировал гипотезу четырех красок так: всякая карта 4-раскрашиваема. Часто пользуются другой формулировкой: всякий планар- ный граф 4-раскрашиваем. В 1890 г. Р. Хивуд показал, что если 4 заменить на 5, то ги- потеза легко доказывается, т. е. верна теорема: всякий планар- ный граф 5-раскрашиваем.
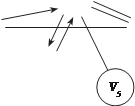
Эйлеровы цепи Как уже упоминалось, с задачи о кенингсбергских мостах началась теория графов. На рис. 1.36 показан план расположе- C
Река Преголь A e D а b f B Рис. 1.36
С роде Кенингсберге (ныне Калининград). g Задача состоит в том, чтобы пройти каж- c d дый мост по одному разу и вернуться в А e D
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.114 (0.265 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
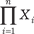 = {(х 1, х 2, …,
= {(х 1, х 2, …,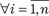 }.
}.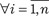

 Е
Е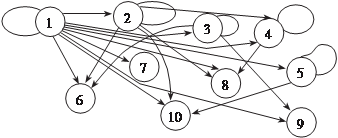
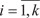 ) можно сделать n i способами, то выбор или А 1 или А 2, …, или А k можно произвести
) можно сделать n i способами, то выбор или А 1 или А 2, …, или А k можно произвести 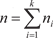 способами.
способами. ) можно сделать m i способами, то выбор и В 1, и В 2, …, и В k можно осуществить
) можно сделать m i способами, то выбор и В 1, и В 2, …, и В k можно осуществить 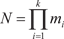 способами.
способами.
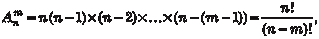
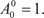
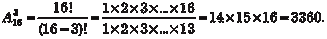
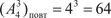

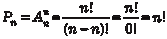
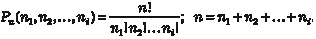
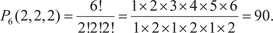
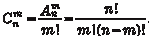
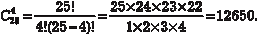
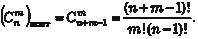

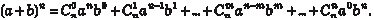

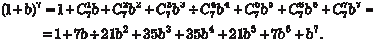

 Е = {(1,2), (1,3), (3,2)}.
Е = {(1,2), (1,3), (3,2)}. определяют ребро e k т. е. e k = (V i, V j) (рис. 1.14).
определяют ребро e k т. е. e k = (V i, V j) (рис. 1.14).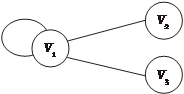 И в этом случае они будут конце- выми вершинами ребра e k. Но конце- вые вершины ребра не обязательно различны, т. е. начальная и ко- нечная вершины могут совпадать.
И в этом случае они будут конце- выми вершинами ребра e k. Но конце- вые вершины ребра не обязательно различны, т. е. начальная и ко- нечная вершины могут совпадать. e k
e k 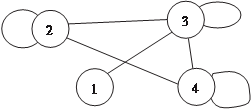

 Рис. 1.17
Рис. 1.17
 Если граф не имеет петель и параллельных ребер его на- зывают простым (см. рис. 1.13).
Если граф не имеет петель и параллельных ребер его на- зывают простым (см. рис. 1.13).






 Если два ребра имеют общую концевую вершину, то они являют- ся смежными (например, ребра e 1 и
Если два ребра имеют общую концевую вершину, то они являют- ся смежными (например, ребра e 1 и

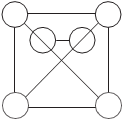
 В тех случаях, когда необхо- димо различать изоморфные гра- фы помечают их вершины и (или) ребра (рис. 1.23).
В тех случаях, когда необхо- димо различать изоморфные гра- фы помечают их вершины и (или) ребра (рис. 1.23).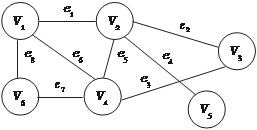


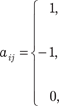


 e 1
e 1
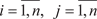 .
.

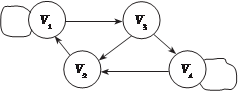 Матрица A s в этом случае будет симметрич- ной относительно главной диагонали. Рассмотрим конкретный пример. Най- дем матрицу смежности
Матрица A s в этом случае будет симметрич- ной относительно главной диагонали. Рассмотрим конкретный пример. Най- дем матрицу смежности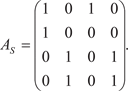

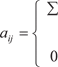
 V 1
V 1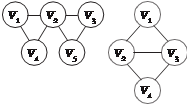

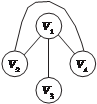
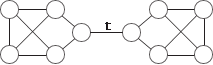
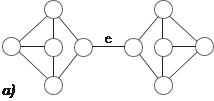 Рис. 1.35
Рис. 1.35 c d g
c d g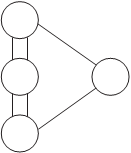 ния семи мостов на реке Преголь в го-
ния семи мостов на реке Преголь в го-


