
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Высказывания и операции над ними
Понятие высказывания является исходным понятием ма- тематической логики. Высказываниями называются повествовательные предло- жения, относительно которых известно или можно определить, истинны они или ложны. Например, предложение “Конго впадает в Тихий оке- ан” — ложное, а предложение “Альтаир — звезда в созвездии Орла” — истинное. Не всякое повествовательное предложение будет высказыванием. В частности, к высказываниям не отно- сятся восклицательные и вопросительные предложения.
Например, не является высказыванием предложение “Ко- торый теперь час?” Не будут высказываниями и предложения, служащие определениями. Например, не будет высказывани- ем предложение “Производной функции у = f (х) называется предел отношения приращения функции к приращению аргу- мента при произвольном стремлении последнего к нулю”. Вы- сказывания будем обозначать заглавными буквами латинского алфавита A, B, C, D, … Из всех свойств высказывания нас ин- тересует только одно: истинно оно или ложно. Каждому истин- ному высказыванию будем сопоставлять 1, а ложному — 0. На множестве всех высказываний введем функцию δ(А), которая принимает значение 1 или 0, т. е. δ(А) назовем значением истинности высказывания А. Например, для высказывания А: “Миссисипи впадает в Бискайский залив” δ(А) = 0. Предположим, что мы имеем начальную совокупность вы- сказываний. Из них с помощью логических операций можно строить новые высказывания. Приведем эти операции. Отрицанием высказывания А называется новое выска- зывание, обозначаемое Таблица 1.15
ния. Таблица 1.15 называется таблицей истинности для отрица-
Конъюнкцией высказываний А и ш является новое выска- зывание (А ∧ В), которое читается “ А и В ”. Таблица истинности для конъюнкции имеет вид (табл. 1.16). Таблица 1.16
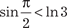 и истинны, т. е. и истинны, т. е.  . .
Дизъюнкцией высказываний А и В называется новое вы- сказывание (А ∨ В), которое читается “ А или В ”. Таблица истинности для дизъюнкции имеет вид (табл. 1.17).
Таблица 1.17
Пример 1.16. Высказывание “В сутках 20 часов или в ми- нуте 60 секунд”. Данное высказывание истинно (несмотря на его странность), так как истинно одно из составляющих его высказываний. Импликацией высказываний А и В называется новое вы- сказывание (А ⇒ В), которое читается “если А, то В или за А следует В ”. Таблица истинности для импликации имеет вид (табл. 1.18).
Таблица 1.18
Пример 1.17. Высказывание “если Земля есть эллипсоид вращения, то log24 = 2” есть импликация высказываний “Земля есть эллипсоид вращения” и “log24 = 2”. Оно является истин- ным, так как истинны оба входящих в него высказывания. Эквивалентностью высказываний А и В называется новое высказывание (А ⇔ В), которое читается “ А эквивалентно В или А тогда и только тогда, когда В ”. Таблица истинности для эквивалентности имеет вид (табл. 1.19). Таблица 1.19
Пример 1.18. Высказывание “Вега находится в созвездии Лиры тогда и только тогда, когда склонение α∪Mi (Полярная) равно 30о” является эквивалентностью двух высказываний “Вега находится в созвездии Лиры” и “склонение α∪Mi (По- лярная) равно 30°”. Оно является ложным, так как первое вы- сказывание истинно, а второе ложно. Число δ(А ⇔ В) полностью определяется δ(А) и δ(В), поэто- му можно оперировать не с высказываниями, а с числами 0 и 1. Например, эквивалентность с помощью 0 и 1 можно записать так: 1 ⇔ 1 = 1; 1 ⇔ 0 = 0; 0 ⇔ 1 = 0; 0 ⇔ 0 = 1. Так же можно поступать и по отношению к другим логичес- ким операциям. Следовательно, каждой логической операции над высказываниями соответствует функция, определенная на множестве {0, 1} и принимающая значения на нем же. Эту функцию называют тем же термином, что и соответствующую логическую операцию. В математической логике с помощью логических операций можно строить формулы. Например, ((А ∧ В) ⇒ С) будет формулой, которая построе- на из высказываний А, В с помощью логических операций ко- нъюнкции и импликации.
Будем называть высказывательными такие переменные, которые могут принимать своими значениями любые конкрет- ные высказывания. Будем обозначать такие переменные заглавными латинс- кими буквами X, Y, Z, U, …. Кроме этого, введем две высказы- вательные переменные И и Л; вместо первой можно подставить любое истинное высказывание, вместо второй — ложное. Следующие соглашения дают описание понятия формулы: а) любая отдельно взятая высказывательная переменная является формулой;
в) не существует никаких других формул, кроме тех, кото- рые получаются в результате применения конечного числа раз пунктов а, б, в. Например, формулами будут Пример 1.19. Рассмотрим формулу ((X ∨ Y) ⇒ Z). Обозначим ее Ф(X, Y, Z). Значение истинности этой формулы полностью оп- ределяется значениями истинности переменных X, Y, Z. Поэто- му можно составить таблицу, дающую значение истинности для Ф(X, Y, Z) в зависимости от значений истинности для X, Y, Z. Так как каждая переменная может принимать два значения (0 и 1), то для тройки X, Y, Z имеем 8 различных возможностей (таблица будет иметь 8 строк). Для заполнения последнего столбца табли- цы подставляем значения X, Y, Z в формулу Ф(X, Y, Z). Например, при X = Y = Z = 1 имеем Ф = ((1∨1) ⇒ 1) = 1. В результате заполнения получим таблицу (см. табл. 1.20)
Таблица 1.20
Для любой формулы Ф(X, Y, Z, …) алгебры высказываний можно составить таблицу, которая дает значение истинности формулы в зависимости от переменных X, Y, Z, …. Эта таблица называется таблицей истинности для формулы Ф(X, Y, Z, …). Таблица 1.20 будет таблицей истинности для формулы ((X ∨ Y) ⇒ Z) в примере 1.19. Определение. Формула Ф(X, Y, Z, …) алгебры высказыва- ний называется тождественно истинной или тавтологией, если ее значение истинности равно 1 при любых значениях истин- ности для X, Y, Z, …. Приведем некоторые важные тавтологии: 1. Законы коммутативности конъюнкции и дизъюнкции: ((X ∧ Y) ⇔ (Y ∧ X)); ((X ∨ Y) ⇔ (Y ∨ X)). 2. Законы ассоциативности конъюнкции и дизъюнкции: (((X ∧ Y)∧ Z) ⇔ (X ∧(Y ∧ Z))); (((X ∨ Y)∨ Z) ⇔ (X ∨(Y ∨ Z))). 3.
; 4. Закон исключения третьего:
5.
. 6.
.
Предикаты В математике используются высказывания, зависящие от одной или нескольких переменных. Например, высказывание log2 x > 3 зависит от переменной х и при различных значени- ях х может быть истинным или ложным. Например, при х = 10 оно превращается в истинное высказывание, а при х = 2 — в ложное. Высказывание 2 х + у > 5 зависит от двух переменных. На- пример, при х = 4 и у = 2 оно будет истинным, а при х = 3 и у = −4 — ложным. Определение. Высказывание, зависящее от переменных x, y, z,… и принимающее значения из некоторого множества D, в математической логике называют предикатом на множестве D. Если предикат содержит одну переменную, то его называ- ют одноместным, а если n переменных, то n-местным. Область D — область определения предиката. Предикаты будем обоз- начать заглавными буквами. Например, B (x) — одноместный предикат, а Р (х, у) — двухместный предикат.
Определение. Подмножество множества D, состоящее из тех значений переменных, при которых данный предикат пре- вращается в истинное высказывание, называют областью ис- тинности предиката. Пример 1.20. Найти область истинности предиката
D: х ≥ −1 — область определения предиката. Область истинности предиката: x ∈ [-1; 8). Предикат на множестве D при подстановке вместо пере- менных конкретных значений становится истинным или лож- ным высказыванием. Поэтому можно считать, что предикат оп- ределен на множестве D и принимает значение на множестве {0, 1}. Поэтому на предикаты распространяются операции над обычными высказываниями.
Задачи для самостоятельного решения 1. Дано: Х = {-5, 17, 22, 34, 101}; Y = {-17, 0, 22, 34, 102, 505}. Найти Х Y, Х Y, Х \ Y, Y \ Х, Х Y. 2. Дано: Х =(-;5]; Y =[-7;607). Найти Х Y, Х Y, Х / Y, Y / Х. 3. Докажите, что отрезки [0,1] и [0,5] равномощны. 4. Дано: Х = {1, 2, 3}; Y = {7, 8} = {(1,7), (1,8), (2,8), (3,7)}. Построить матрицу и граф отношения. 5. Сколькими способами в отделе, состоящем из 100 чело- век можно выбрать начальника и его заместителей? 6. Есть шесть видов конвертов без марок. Сколькими спо- собами можно выбрать конверт и марку для отправки письма? 7. Из двенадцати человек надо выбрать пять и разместить их на занумерованных стульях (по одному человеку на стул). Сколькими способами это можно сделать? 8. Сколькими способами можно посадить за стол четырех мужчин и четырех женщин так, чтобы женщины и мужчины не сидели рядом? 9. Сколько различных восьмизначных чисел можно соста- вить, используя цифры 3,4,5? 10.
Найти матрицы инцидентности для двух графов: 11.
Найти матрицы смежности для графов: 11. Найти таблицы истинности для формул 11.1.
12. Доказать, что формула 13. Найти область истинности предиката Q (x) = log3(x + + 2) < 4.
Вопросы для самопроверки 1. Какие способы задания множеств вы знаете? 2. Какое множество называется универсальным? 3. Какое отношение называется бинарным? 4. Что называется числом сочетаний из n элементов по m? 5. Что называется числом размещений из n элементов по m? 6. Что называется перестановкой из n элементов? 7. Какие графы называются изоморфными? 8. Какие графы называются Эйлеровыми? 9. Что такое степень вершины графа?
10. Какие графы называют деревьями? 11. Что такое k -раскраски графа? 12. Какие графы называют планарными? 13. Какой граф называется гамильтоновым? 14. Какие из графов правильных многогранников имеют гамильтоновы циклы? 15. Какие предложения называются высказываниями? 16. Привести определения логических операций. 17. Какие формулы алгебры высказываний называются тавтологиями? 18. Какие высказывания называются предикатами? 19. Что называется областью истинности предиката?
Глава 2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ Линейная алгебра — это часть математики, посвященная в основном теории матриц и связанной с нею теории линейных преобразований, векторных пространств. Она включает теорию форм, теорию инвариантов, тензорную алгебру. В данном учебнике мы рассмотрим понятие матрицы, ее применение для решения систем линейных алгебраических уравнений (СЛАУ), а также определители, векторы, собствен- ные числа, векторы матриц и квадратичные формы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.247 (0.069 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

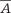 , которое читается “не А или невер- но, что А”. А и
, которое читается “не А или невер- но, что А”. А и 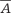 связаны между собой следующим образом (табл. 1.15).
связаны между собой следующим образом (табл. 1.15). )
)
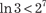
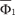

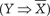 , ((X ⇔ Y) ⇒ Z), а вы- ражение
, ((X ⇔ Y) ⇒ Z), а вы- ражение  формулой не является.
формулой не является.
 .
.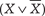 .
.
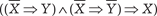
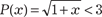 .
.
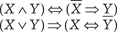
 является тавтологией.
является тавтологией.


