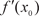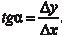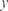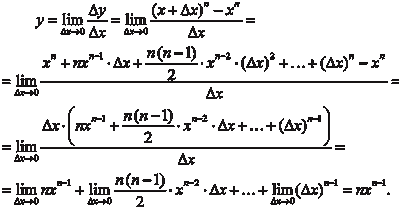Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Основы дифференциального исчисления
Дифференциальное исчисление — это раздел математи- ческого анализа, связанный в основном с понятиями производ- ной и дифференциала функции.
Производная первого порядка. Дифференциал. Производные высших порядков
Производной функции y = f (x) называется предел отноше- ния приращения функции к приращению аргумента при про- извольном стремлении последнего к нулю. т. е. производная функции
есть некоторая функция, полученная по определенным прави- лам из заданной функции. Значение производной функции y = f (x) в какой-то точке x 0 обозначают обычно так: f (x 0) или Механический смысл производной — это предел средней скорости за бесконечно малый промежуток времени, т. е. мгно- венная скорость. Геометрический смысл производной вытекает из следую- щей теоремы.
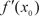 , яв- ляется касательной к графику функции в точке M 0. , яв- ляется касательной к графику функции в точке M 0.
Геометрический смысл производной иллюстрируется на рис. 4.1.
Рис. 4.1
Проведем через точки M 0 и M 1 секущую, угол между се- кущей и положительным направлением оси 0 x равен: Будем перемещать точку M 1 по кривой в сторону точки M 0 т. е. устремим x к нулю. Предельным значением секущей бу- дет касательная, проходящая через точку M 0. Тогда получим:
Установим связь между непрерывностью и дифференци- руемостью функции. Она видна из следующей теоремы,
Рис. 4.2
Из определения производной следует способ ее вычисления.
Найдем производную функции y = xn, где n Z, исходя из определения производной Итак, (x n) = nx n −1, например (x 8) = 8 x 7. Можно доказать, что полученная формула верна для всех n R [42, 44]. Из приведенного примера видно, что использовать оп- ределение производной для ее вычисления дело достаточно трудоемкое. Поэтому гораздо проще, используя определение производной, вывести производные основных элементарных функций и сформулировать правила дифференцирования ал- гебраической суммы, произведения, частного функций, слож- ной функции, обратной функции. По полученным формулам и правилам можно будет находить производные любых элемен- тарных функций.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.16 (0.005 с.) |
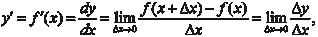
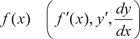
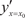 .
.