Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление двойного интеграла
1. Простейший случай.
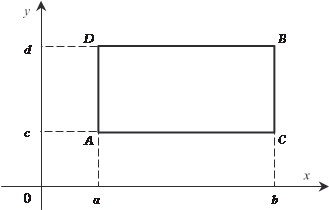
Область В задана неравенствами a x b, c y d, т. е. она является прямоугольником ADBC (рис. 5.28). Рис. 5.28 В этом случаи двойной интеграл вычисляется по одной из приводимых ниже формул:
(5.26)
В правых частях формул (5.25) и (5.26) стоят повторные ин- тегралы.
ределенный интеграл , причем у рассматривается как постоянная, но результат интегрирования рассматривается как функция от у. Второе интегрирование в пределах от с до d выполняется по аргументу у. При использовании формулы (5.26) порядок действий обратный.
кого тела с основанием ADBC. Заметим, что внешние знаки ин- теграла соответствуют внешним дифференциалам. Рассмотрим конкретные примеры. Вычислить интегралы:
Пример 5.49.
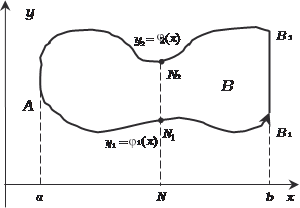
2. Общий случай. а) Если контур области В встречается с любой пересека- ющей его вертикальной прямой не более чем в двух точках (т. N 1 и т. N 2 на рис. 5.29), то область В задается неравенствами a x b и 1(х) y 2(х),
Рис. 5.29 где a и b — крайние абсциссы области В; 1(х) и 2(х) — функции, выражающие ординаты нижней и верхней граничных линий AN 1 B 1 и AN 2 B 2. В этом случае двойной интеграл находится по формуле [9, 44]:
(5.28)
Если контур области В не подходит ни под случай а), ни под случай б), то ее разбивают на несколько частей так, чтобы к каждой части были применимы или формула (5.27) или (5.28).
d x 2 = 2(y) K 1 K 2 K B x 1 = 1(y)
c C 0 x Рис. 5.30 Рассмотрим конкретный пример. Пример 5.50.
Вычислим интеграл 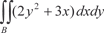 , если область В огра- ничена линиями у = х 2, у 2 = х (рис. 5.31). Данная задача подхо- дит под случаи а) и б). , если область В огра- ничена линиями у = х 2, у 2 = х (рис. 5.31). Данная задача подхо- дит под случаи а) и б).
Рис. 5.31 Используем, например, формулу (5.27) (случай а). В дан- ном случае а = 0, b = 1, 1(х) = х 2,
Пример 5.51. Вычислить двойной интеграл ограничена следующими линиями: у = х 2 и х + у − 2 = 0. Строим область интегрирования В (рис. 5.32).
Рис. 5.32
Используя формулу (5.27) получаем:
Пример 5.52.
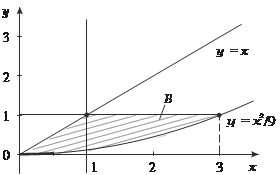
Поменять порядок интегрирования в повторном интеграле Из исходных данных следует, что область интегрирования В ограничена линиями х = 0, х = 1, х = 3, у = х 2/9, у = х, у =1. Построим область интегрирования В (рис. 5.33).
Рис. 5.33
Область интегрирования В является правильной в направ- лении параллельном направлению оси 0 Х, поэтому в соответс- твии с формулой (5.28) получаем Замена переменной в двойном интеграле К замене переменной прибегают для того, чтобы упростить нахождение двойного интеграла. Предположим, что аргументы х и у функции z = f (x i y) связаны с переменными U и V следую- щими соотношениями: x = ϕ(U, V), y = ψ(U, V), т. е. z = (ϕ(U, V),
. (5.29)
В этом случае верна следующая формула замены пере- менных в двойном интеграле, которую мы приводим без дока- зательства:
Пределы в двойном интеграле по области В ′ расставляют- ся таким же образом, как и в двойном интеграле по области В с учетом геометрии этой области. Рассмотрим отдельно част- ный случай замены переменных, часто применяемый при вы- числении двойного интеграла, а именно переход от декартовых прямоугольных координат (х, у) к полярным координатам (r, ϕ). Напомним, что прямоугольные и полярные координаты связа- ны между собой следующими формулами: х = r ·cosϕ, y = r ·sinϕ, где r ≥ 0, 0 ≤ ϕ ≤ 2π. Находим якобиан этого преобразования: Теперь используя формулу (5.29), получаем:
Следовательно, формула перехода от декартовых коорди- нат к полярным имеет вид:
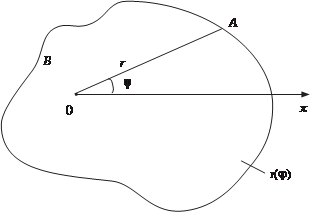
где B ′ — область в полярной системе координат, соответствую- щая области В в прямоугольной системе координат. На практике переход к полярной системе координат осу- ществляют по формулам: х = r cosϕ, y = r sinϕ, dxdy = rdrd ϕ. Урав- нение линий, ограничивающих область В также преобразуют к полярным координатам. Преобразование области В в область В ′ не проводят, а совмещая полярную и прямоугольную системы координат находят пределы интегрирования по r и ϕ. Заметим, что переход от двойных интегралов к повторным в правой части формулы (5.31) приводит к разным пределам в зависимости от того, где находится полюс полярной системы координат. Если полюс (т. 0) полярной си- стемы координат находит- ся вне области В, которая ограничена лучами ϕ = α и ϕ = β (α > β) и функция- B
r 2 ( ϕ ) ми r 1(ϕ) и r 2(ϕ) (r 1(ϕ) < r 2(ϕ)) (рис. 5.34), то двойной ин- теграл в полярных коор- динатах приводится к по- вторному по следующей формуле: a
β Рис. 5.34
В том случае если полюс (т. 0) находится внутри области В (рис. 5.35) и уравнение границы области в полярной системе ко- ординат имеет вид r (ϕ), то в формуле (5.32) α = 0, β = 2π, r 1(ϕ) = 0, r 2(ϕ) = r (ϕ) и формула 5.32 принимает вид:
Когда полюс (т. 0) находится на границе области В и урав- нение этой границы в полярной системе координат имеет вид r (ϕ), то в формуле (5.32) r 1(ϕ) = 0, r 2(ϕ) = r (ϕ), а углы α и β могут принимать различные значения (рис. 5.36).
Рис. 5.35
Рис. 5.36 Заметим, что переход к полярным координатам часто ис- пользуется в том случае, если подынтегральная функция име- ет вид f (x 2 + y 2), а область интегрирования В есть круг, кольцо или их части. В ряде случаев, например, когда область интегрирова- ния В — эллипс или его часть, используют переход от прямо- угольных к обобщенным полярным координатам. Связь меж- ду этими системами координат осуществляется по формулам: x = ar cosϕ, y = br sinϕ, где r ≥ 0, 0 ≤ ϕ ≤ 2π, a ∈ R, b ∈ R. Якобиан данного преобразования (см. (5.29)) будет иметь вид:
Следовательно, искомая формула перехода такова:
В ′ — область в обобщенной полярной системе координат, соответствующая области В. Рассмотрим несколько конкретных примеров. Пример 5.53. Вычислить двойной интеграл
Область интегрирования В данного примера не является правильной ни по направлению оси 0 Х, ни по направлению оси 0 Y. Поэтому для того, чтобы облегчить «взятие» исходного ин- теграла, сделаем замену переменной. Положим: U = y − 2 x; V = y + x. Тогда получим: U = -3; U = 5; V = 7; V = -1. Область В в системе координат 0 ХY перейдет в область В ′ в системе координат 0′ UV (рис. 5.38). Из рис. 5.38 видно, что об- ласть В ′ является простейшей, поэтому для вычисления двой- ного интеграла по этой области можно использовать или фор- мулу (5.25) или формулу (5.26).
Рис. 5.38 Выражаем х и у через U и V. Получаем x = - U /3+ V /3; y = U /3 + 2/3 · V.
Находим якобиан преобразования по формуле (5.29): Следовательно, исходный двойной интеграл будет равен:
Вычислить двойной интеграл , если об- ласть В интегрирования ограничена линией х 2 + у 2 ≤ 25.
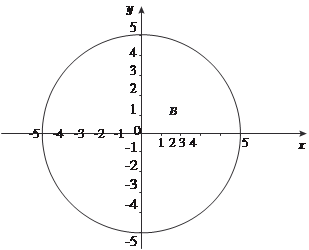
Так как область интегрирования представляет собой ок- ружность (рис. 5.39),то для вычисления исходного интеграла гораздо рациональнее перейти к полярной системе коорди- нат. Тогда получаем x = r cosϕ, y = r sinϕ, I (U, V) = rA. Исходный двойной интеграл будет равен: Если не переходить к полярным координатам, а воспользо- ваться формулой (5.27),то будем иметь:
Видно, что полученный интеграл будет решаться значи- тельно дольше, а замена переменной сильно упрощает процесс решения.
Рис. 5.39 Пример 5.55. Вычислить двойной интеграл Область В представляет собой эллипс (рис. 5.40). Для того чтобы упростить решение исходного двойного интеграла, го- раздо рациональнее перейти к обобщенной полярной системе координат.
Получим x = 2 r · cosϕ (а = 2), y = 3 r · sinϕ (b = 3), I (U, V) = 6 r, dxdy = 6 rdrd ϕ. Получим уравнение эллипса в обобщенных по- лярных координатах: r 2 · cos2ϕ + r 2 · sin2ϕ =1. r = 1. Следовательно r будет меняться от 0 до 1, а ϕ от 0 до 2π. Исходный двойной интеграл будет равен:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.42 (0.074 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
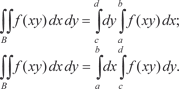 (5.25)
(5.25)
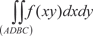

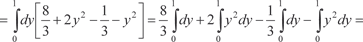
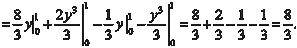
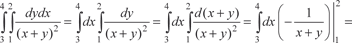
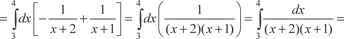
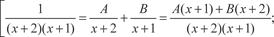
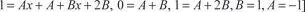 , получаем
, получаем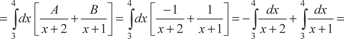
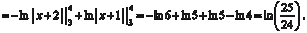
 0
0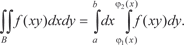

 y D
y D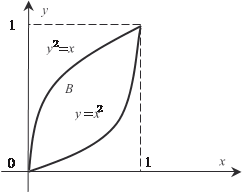
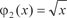 . Поэтому получим:
. Поэтому получим: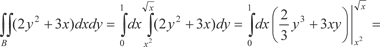

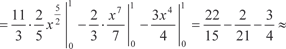

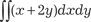 , если область В
, если область В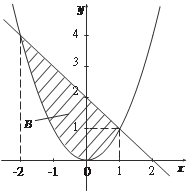
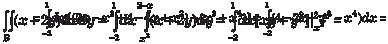
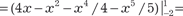
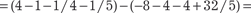
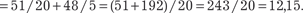
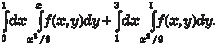

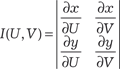
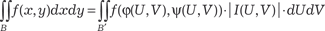
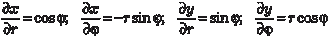
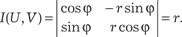

 r 1 ( ϕ )
r 1 ( ϕ ) 0
0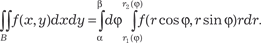
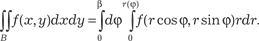

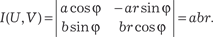

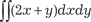 , если область В ограничена линиями: у = 2 х − 3, у = 2 х + 5, у = - х + 7, у = - х − 1. Данная область в декартовой системе координат будет иметь вид (рис. 5.37).
, если область В ограничена линиями: у = 2 х − 3, у = 2 х + 5, у = - х + 7, у = - х − 1. Данная область в декартовой системе координат будет иметь вид (рис. 5.37).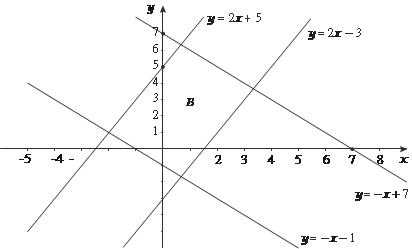


 Рис. 5.37
Рис. 5.37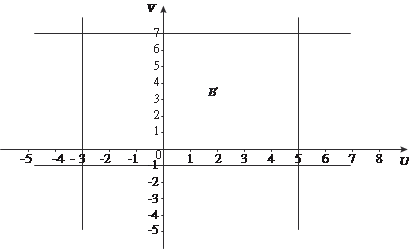

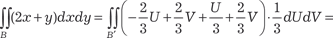

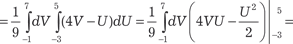
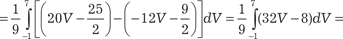
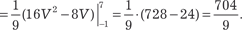
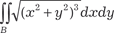
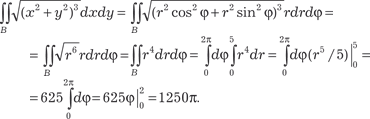

 , если область В ог- раничена линией: х 2/4 + у 2/9 ≤ 1.
, если область В ог- раничена линией: х 2/4 + у 2/9 ≤ 1.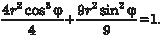
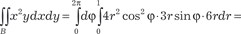
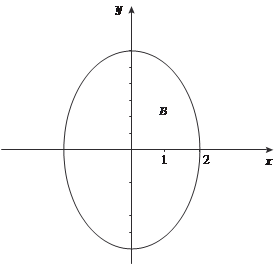 Рис. 5.40
Рис. 5.40