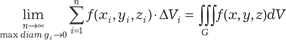Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые приложения двойного интеграла
Мы уже говорили о том, что геометрический смысл двой- ного интеграла — это объем цилиндрического тела. Поэтому будет верна следующая формула:
где f (x, y) — уравнение поверхности, которая ограничивает тело; В — проекция поверхности f(x,y) на плоскость 0 ХУ. Если положить в формуле (5.35) f (x, y) = 1, то цилиндри- ческое тело превратится в прямой цилиндр высотой, равной единице. Его объем будет равен площади (S) основания В. Поэ- тому получаем формулу для определения площади области В:
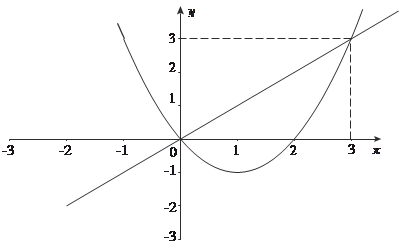
Приведем некоторые примеры. Пример 5.56. Найти площадь фигуры, ограниченной линиями у = х 2 − 2 х; у = х.
Построим фигуру В и найдем пределы интегрирования (рис. 5.41). Используем формулу (5.36) и получаем:
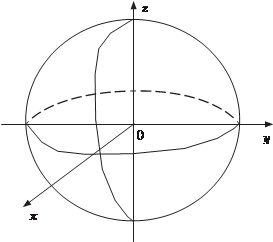
Пример 5.57. Рис. 5.41 Найдем объем шара, ограниченного сферой радиуса R (рис. 5.42).
или .
Рис. 5.42
Проекция на плоскость 0ХУ — это окружность х 2 + у 2 = R 2 или Теперь по формуле (5.35) по- лучаем:
Чтобы упростить вычисления полученного повторного ин- теграла, перейдем к полярной системе координат: y = r · sinϕ, x = r · cosϕ, dхdy = rdrd ϕ.
Тогда получаем:
Cледовательно, искомый объем шара будет равен V = 4/3π R 3.
Некоторые сведения о тройном интеграле Тройной интеграл является обобщением определенного интеграла на случай функции трех независимых аргументов. К понятию тройного интеграла можно прийти, рассматривая, например, задачу о нахождении массы неоднородного тела.
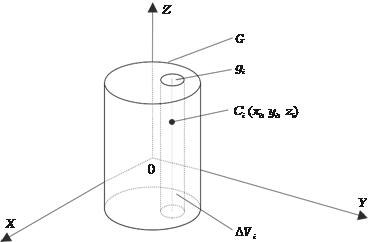
Предположим, что имеется некоторое тело, которое зани- мает пространственную область G (рис. 5.44), а плотность рас- пределения массы в этом теле — непрерывная функция коор- динат точек этого тела, т. е. ρ = ρ(x, y, z) [9, 48].
Рис. 5.44 Произвольно разобьем данное тело на n частей g 1, g 2, …, g n. Их объемы обозначим ∆ V 1, ∆ V 2, …, ∆ V n. Выберем в этих частях
точки C 1(x 1, y 1, z 1), C 2(x 2, y 2, z 2), …, C n (x n, y n, z n). Далее, предпо- лагая, что в каждой из частей плотность постоянна и равна ее значению в точке
Предел суммы (5.37) в том случае, если n → ∞ и максималь- ный диаметр каждой части стремится к нулю, и есть масса ис- ходного тела, т. е.
Сумма (5.37) называется n -й интегральной суммой, а ее предел (5.38) — тройным интегралом от функции ρ(x, y, z) по области G.
и найдем ее предел при стремлении n → ∞ и максимального диаметра каждой части к нулю. Этот предел и называют тройным интегралом от функции W = f (x, y, z) по области G и обозначают следующим образом:
где f (x, y, z) — подынтегральная функция; dV — элемент объема. Теперь сформулируем теорему о существовании тройного интеграла. Теорема 5.5. Если функция W = f (x, y, z) непрерывна в ог- раниченной замкнутой области G, то существует предел интег- ральной суммы (5.39) при n → ∞ и max diam g i → 0 и этот предел (тройной интеграл) не зависит от метода разбиения области G на части g i и от выбора точек C i (x i, y i, z i) в них. Свойства тройных интегралов полностью совпадают со свойствами двойных интегралов, некоторые из которых пере- числены в подразд. 5.6.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.95.244 (0.009 с.) |
 , (5.35)
, (5.35)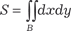
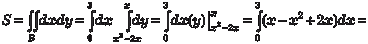


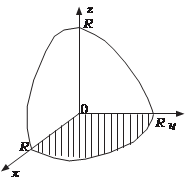 Шар — фигура симметрич- ная. Поэтому вычислим объем 1/8 его части, которая лежит в первом октанте (рис. 5.43).
Шар — фигура симметрич- ная. Поэтому вычислим объем 1/8 его части, которая лежит в первом октанте (рис. 5.43).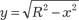 .
.
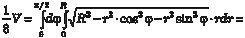
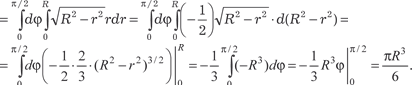
 , запишем приближенную формулу для массы всего тела [9, 48]:
, запишем приближенную формулу для массы всего тела [9, 48]: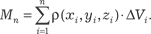
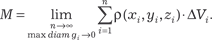
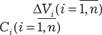 К вычислению тройного интеграла приводит, кроме рас- сматриваемой нами задачи, и ряд других задач. Теперь рас- смотрим непрерывную в области G функцию W = f (x, y, z). Ра- зобьем область G на n частей g i объемами и в каждой части выберем произвольную точку . Составим интег- ральную сумму
К вычислению тройного интеграла приводит, кроме рас- сматриваемой нами задачи, и ряд других задач. Теперь рас- смотрим непрерывную в области G функцию W = f (x, y, z). Ра- зобьем область G на n частей g i объемами и в каждой части выберем произвольную точку . Составим интег- ральную сумму (5.39)
(5.39)