
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок аппроксимации разностной схемы. Оценка порядка аппроксимации разностной схемы с весами для нестационарного уравнения теплопроводности.Содержание книги
Поиск на нашем сайте Построение разностной схемы состоит из последовательности стандартных шагов. - Построение сетки в области определения искомого решения задачи. - Замена в ДУ непрерывных производных их разностными аналогами. - Замена всех функций соответствующими сеточными функциями, определенными в узлах =>приходим к разностной схеме, представляющей дискретный аналог дифференциальной задачи и содержащей шаги сетки. Решение разностной задачи Разностная схема имеет
Разность между дискретными и непрерывными производными принято называть погрешностью аппроксимации или ошибкой дискретизации дифференциального оператора на данной функции. Погрешность аппроксимации дифференциальных операторов может быть выражена путем разложения дифференцируемой функции в степенной ряд в окрестности фиксированного узла сетки (если возможно). Погрешность аппроксимации дискретной модели складывается из погрешностей аппроксимации каждого из ее элементов (погрешности аппроксимации производных, граничных условий, коэффициентов, функций и т.п.). Разностная схема аппроксимирует дифференциальную задачу, если погрешность аппроксимации данной разностной схемы на решении дифференциальной задачи стремиться к нулю при шагах сетки, стремящихся к нулю. Следует подчеркнуть отличие понятий погрешности приближенного решения и погрешности аппроксимации задачи. Погрешность решения определяется разностью между точным решением и некоторым его приближением. Погрешность аппроксимации дискретной задачи выражает невязку, которая возникают при подстановке точного решения в уравнения дискретной задачи, характеризует величину возмущений, связанных с переходом от дифференциальной модели к дискретной.
Рассмотрим стандартную процедуру оценки порядка аппроксимации разностных схем, для дифференциального уравнения вида
1)Изобразить шаблон, выбрать точку, относительно которой будем искать невязку. Если шаблон симметричен - относительно центра симметрии. Если несимметричен - в какой-то внутренней точке шаблона, отн-но которой имеет место хотя бы частичная симметрия. 2)Подставить точное решения в построенную схему, полагая, что в точке, относительно которой мы намерены вычислить невязку, значение решения известно, а во всех других точках шаблона зн-я данного реш-я выразить с помощью конечного числа ряда Тейлора. 3)Привести всё к виду 4)Оценить порядок малости невязки
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

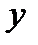 сходится к решению дифф. задачи
сходится к решению дифф. задачи 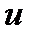 , если при шагах сетки, стремящихся к нулю
, если при шагах сетки, стремящихся к нулю 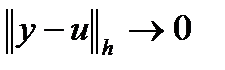 ,
,  в пространстве сеточных функций.
в пространстве сеточных функций.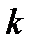 -й порядок аппроксимации по шагу h (или
-й порядок аппроксимации по шагу h (или 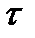 ), если при убывании шагов сетки погрешность аппроксимации стремиться к нулю как
), если при убывании шагов сетки погрешность аппроксимации стремиться к нулю как 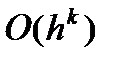 (
( ).
). ,
, 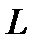 - дифференциальный оператор, содержащий частные производные по всем независимым переменным. Разностную аппроксимацию данного уравнения можно представить в виде
- дифференциальный оператор, содержащий частные производные по всем независимым переменным. Разностную аппроксимацию данного уравнения можно представить в виде 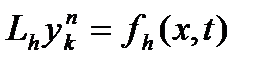 ,
,  ,
, 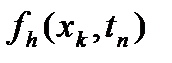 - сеточные представления дифференц-х операторов и функции правой части.
- сеточные представления дифференц-х операторов и функции правой части.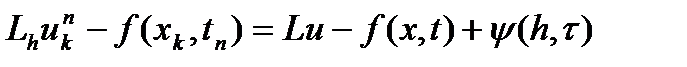 .
.  относительно шагов сетки.
относительно шагов сетки.


