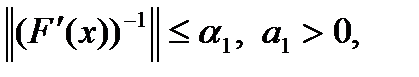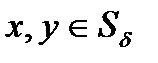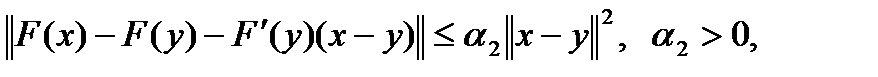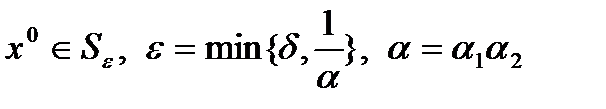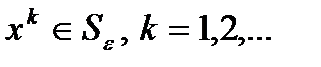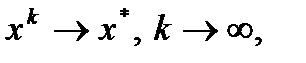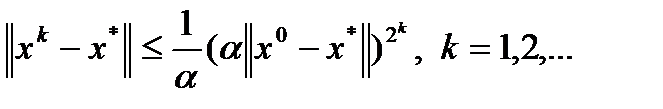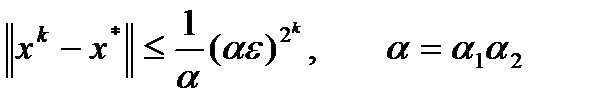Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Итерационные методы решения нелинейных уравнений. Метод Ньютона.
В отличие от систем линейных алгебраических уравнений, для решения которых могут применяться как прямые (или точные), так и итерационные (или приближенные) методы, решение систем нелинейных уравнений можно получить только приближенными, итерационными методами. Они позволяют получать последовательность приближений Рассмотрим нелинейную систему уравнений (1) Она может быть также представлена в матричном виде:
Её решением называется такое значение Если для посл. xn, сходящейся к х*, верна формула: (k – положит-е действ-е число), то k - скорость сходимости данной последовательности. Итерационные методы решения систем нелинейных уравнений: метод простых итераций, преобразование Эйткена, метод Ньютона, метод градиентного спуска, метод Пикара Метод Ньютона Основная идея метода Ньютона состоит в выделении из уравнений линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем. Рассмотрим систему уравнений: в предположении, что Полагая Опишем общий шаг метода. Пусть уже получено приближение Очередное приближение Если матрица Якоби Таким образом, в основе метода Ньютона лежит идея линеаризации вектор-функции Через уже известное приближение
Точное условие сходимости метода Ньютона имеет достаточно сложный вид. Но очевидный результат: в достаточно малой окрестности корня итерации сходятся, если матрица Якоби невырожденная, причём сходимость квадратичная. Пусть в
Теорема (о сходимости). Пусть 1) вектор-функция 2) для всех 3) для всех 4) Тогда метод Ньютона (3) 1) 2) 3) Замечание. Оценка погрешности метода Ньютона:
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.93.44 (0.007 с.) |
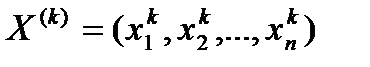
 . Если итерационный процесс сходится, то граничное значение
. Если итерационный процесс сходится, то граничное значение 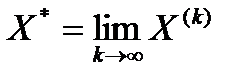 является решением данной системы уравнений.
является решением данной системы уравнений.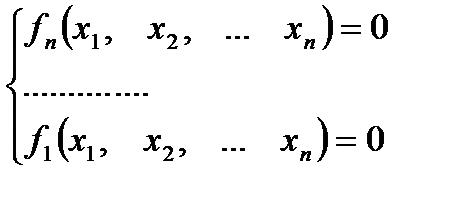
 (1’), где
(1’), где
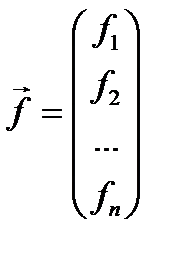
 , для котрого
, для котрого 

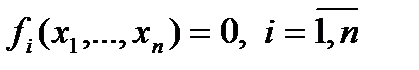
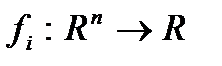 – непрерывно-дифференцируемые функции.
– непрерывно-дифференцируемые функции.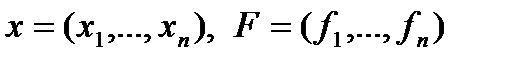 , перейдём к векторной записи
, перейдём к векторной записи 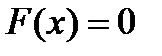 (2)
(2)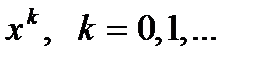 Разложим функцию
Разложим функцию 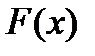 в ряд Тейлора, оставив только два первых члена в силу малости отклонения приближения
в ряд Тейлора, оставив только два первых члена в силу малости отклонения приближения 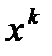 от корня:
от корня: 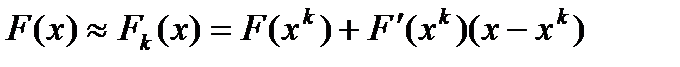 ,
, 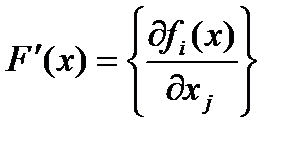 – матрица Якоби для
– матрица Якоби для 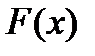 .
.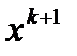 определяется как решение линейной системы
определяется как решение линейной системы 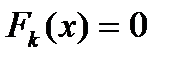 , т.е.
, т.е. 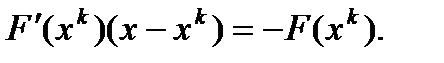
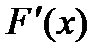 не вырождена, то решение системы линейной системы можно записать в явном виде, что приводит к стандартной формуле метода Ньютона
не вырождена, то решение системы линейной системы можно записать в явном виде, что приводит к стандартной формуле метода Ньютона 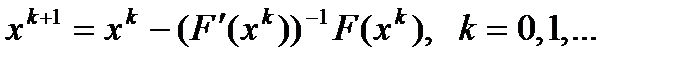 (3)
(3)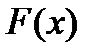 в окрестности каждого приближения (на каждой итерации), что позволяет свести решение системы (2) к последовательному решению линейных систем.
в окрестности каждого приближения (на каждой итерации), что позволяет свести решение системы (2) к последовательному решению линейных систем.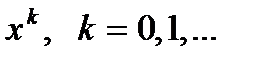 к корню
к корню 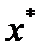 можно записать, что
можно записать, что 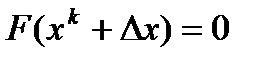 , где
, где 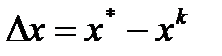 . Тогда после линеаризации получим систему уравнений, линейную относительно
. Тогда после линеаризации получим систему уравнений, линейную относительно 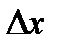 . Таким образом, на каждом шаге мы будем находить приращения
. Таким образом, на каждом шаге мы будем находить приращения 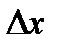 , и новое приближение к решению по формулам:
, и новое приближение к решению по формулам: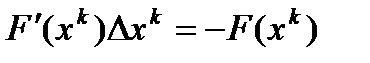 – система линейных уравнений.
– система линейных уравнений.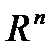 выбрана нек-я векторная
выбрана нек-я векторная 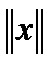 и согласованная с ней матричная
и согласованная с ней матричная 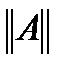 .
.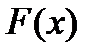 определена и непрерывно-дифференцируема в области
определена и непрерывно-дифференцируема в области 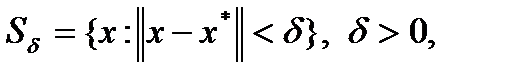 где
где 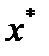 – решение уравнения (2),
– решение уравнения (2),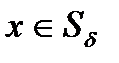 существует обратная матрица
существует обратная матрица 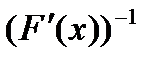 , причём
, причём