
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
Решение разностной задачи Разностная схема имеет Разность между дискретными и непрерывными производными принято называть погрешностью аппроксимации или ошибкой дискретизации дифференциального оператора на данной функции. Погрешность аппроксимации дифференциальных операторов может быть выражена путем разложения дифференцируемой функции в степенной ряд в окрестности фиксированного узла сетки (если возможно). Погрешность аппроксимации дискретной модели складывается из погрешностей аппроксимации каждого из ее элементов (погрешности аппроксимации производных, граничных условий, коэффициентов, функций и т.п.). Разностная схема аппроксимирует дифференциальную задачу, если погрешность аппроксимации данной разностной схемы на решении дифференциальной задачи стремиться к нулю при шагах сетки, стремящихся к нулю. Следует подчеркнуть отличие понятий погрешности приближенного решения и погрешности аппроксимации задачи. Погрешность решения определяется разностью между точным решением и некоторым его приближением. Погрешность аппроксимации дискретной задачи выражает невязку, которая возникают при подстановке точного решения в уравнения дискретной задачи, характеризует величину возмущений, связанных с переходом от дифференциальной модели к дискретной.
!!Устойчивость дискретной модели не следует из устойчивости дифференциальной задачи, которую данная дискретная модель аппроксимирует. Разностная схема называется устойчивой, если ее решение непрерывно зависит от входных данных, т. е. малому изменению входных данных соответствует малое изменение решения. Устойчивость характеризует чувствительность разностной схемы к различного рода погрешностям, она является внутренним свойством разностной задачи, и это свойство не связывается непосредственно с исходной дифференциальной задачей (в отличие от сходимости).
Устойчивость бывает условной и безусловной в зависимости от того, накладываются ли ограничения на соотношения между шагами по разным переменным. Если решение исходной дифференциальной задачи существует, а разностная схема устойчива и аппроксимирует задачу, то разностное решение сходится к точному. Для доказательства устойчивости дискретной модели M – постоянная, не зависящая от шагов сетки. Это неравенство фактически означает непрерывную зависимость приближенного решения от правой части. Произвольное частное решение дискретной задачи ищется в виде Подстановка такой сеточной функции в разностное уравнение позволяет определить, при каких значениях - Если - Если же, напротив, для некоторого значения
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.122 (0.008 с.) |
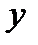 сходится к решению дифференциальной задачи
сходится к решению дифференциальной задачи 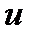 ,если при
,если при 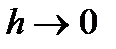
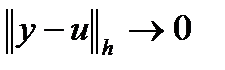 , где
, где  некоторая норма в пространстве сеточных функций.
некоторая норма в пространстве сеточных функций.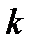 -й порядок точности по шагу h (или h и
-й порядок точности по шагу h (или h и 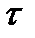 ), если для погрешности приближенного решения
), если для погрешности приближенного решения  при любых достаточно малых шагах сетки выполняется оценка
при любых достаточно малых шагах сетки выполняется оценка 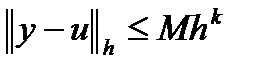 , (или
, (или 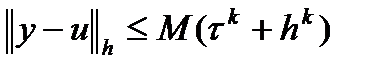 ). Порядок точности разностных схем относительно шагов сетки по пространственной и временной переменной, вообще говоря, не обязательно совпадает.
). Порядок точности разностных схем относительно шагов сетки по пространственной и временной переменной, вообще говоря, не обязательно совпадает.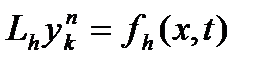 достаточно доказать, что приближенное решение удовлетворяет неравенству
достаточно доказать, что приближенное решение удовлетворяет неравенству 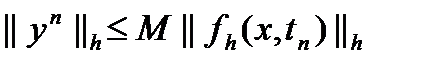 ,
,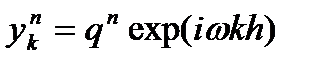
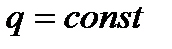 данная сеточная функция удовлетворяет разностному уравнению.
данная сеточная функция удовлетворяет разностному уравнению.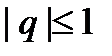 для произвольных действительных
для произвольных действительных 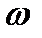 , данное решение будет устойчивым.
, данное решение будет устойчивым. мы получим
мы получим 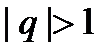 , то такое частное решение будет неограниченно возрастать при
, то такое частное решение будет неограниченно возрастать при 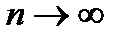 , т.е. является неустойчивым.
, т.е. является неустойчивым.


