
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямой метод вычисления собственных значений:
В прямом методе получают хар-е ур-е в аналитическом виде или определяют алгоритм выч-я коэфф-в уравнения, потом решают это ур-е одним из численных методов. det(A- λ E) = D (λ) может быть представлен в виде D (λ) =
Наиболее эффективный подход к проблеме собственных значений основан на использовании преобразований подобия, позволяющих привести исходную матрицу к треугольному, диагональному или блочно-диагональному виду. Поскольку преобразование подобия не меняет спектр матрицы, то применение такого рода преобразований во многих случаях приводит к решению полной проблемы собственных значений. Наиболее эффективны преобразования подобия в случае симметричных матриц. Однако во многих случаях достаточно предположить, что среди собственных значений матрицы отсутствуют кратные. В этом случае существует преобразование подобие, приводящее матрицу к диагональному виду. Способ построения преобразования подобия: исп-е элем-х матриц плоских вращений Матрица
Определим угол вращения таким образом, чтобы Используя тригонометрические тождества, имеем:
При выбранном угле поворота в результате преобразования
Метод Данилевского: Большая погрешность, но большая скорость получения результата.
Метод основан на известном факте из линейной алгебры о том, что преобразование подобия
( Приводим матрицу Для матрицы => элементы 1-й строки Решив полученное уравнение Построение матрицы
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.114.38 (0.006 с.) |

 - сумма всех диагональных миноров первого порядка матрицы А.
- сумма всех диагональных миноров первого порядка матрицы А. - cумма всех диагональных миноров второго порядка.
- cумма всех диагональных миноров второго порядка.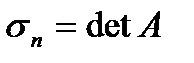 . Вычислив
. Вычислив  , находим корни полинома одним из численных методов.
, находим корни полинома одним из численных методов. :
: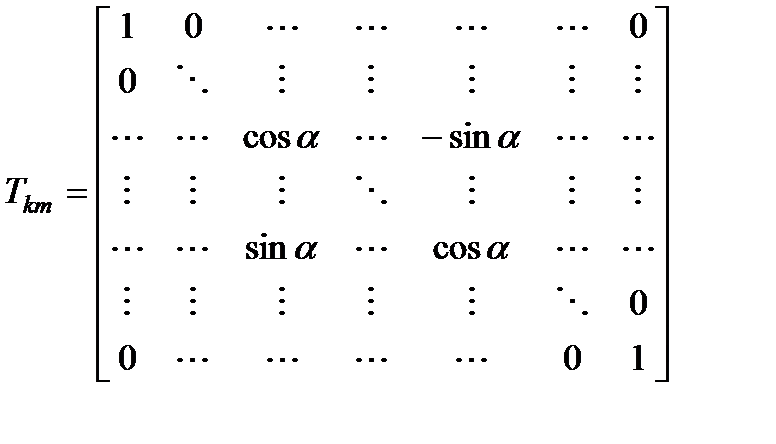 (3)
(3) ) отличается от единичной матрицы только элементами
) отличается от единичной матрицы только элементами  и
и  .
.  - преобразование плоских вращений, является преобразованием подобия. При умножении матрицы слева (справа) на
- преобразование плоских вращений, является преобразованием подобия. При умножении матрицы слева (справа) на  и
и  (столбцами). Полагая
(столбцами). Полагая  , рассмотрим произведения:
, рассмотрим произведения: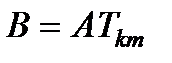 :
:  ,
,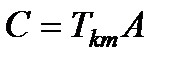 :
:  .
.
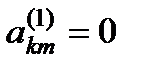 .
.  .
. ,
,  . (4)
. (4) , приводит к сходимости последовательности матриц
, приводит к сходимости последовательности матриц 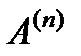 ,
,  к матрице диагонального вида, при этом на диагонали новой матрицы будут находиться приближенные значения собственных чисел исходной матрицы
к матрице диагонального вида, при этом на диагонали новой матрицы будут находиться приближенные значения собственных чисел исходной матрицы  .
. 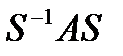 не меняет характеристического многочлена матрицы
не меняет характеристического многочлена матрицы 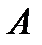 , т.к.
, т.к. .
. => при записи характер-го уравнения на него сокращаем).
=> при записи характер-го уравнения на него сокращаем). к так называемой канонической форме Фробениуса:
к так называемой канонической форме Фробениуса: 
 характеристический многочлен может быть легко записан, если последовательно разлагать определитель
характеристический многочлен может быть легко записан, если последовательно разлагать определитель  по элементам первого столбца =>
по элементам первого столбца => 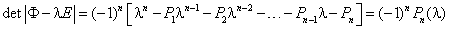
 являются коэффициентами её собственного многочлена => собственного многочлена матрицы
являются коэффициентами её собственного многочлена => собственного многочлена матрицы  .
. 
 , находим собственные значения матрицы
, находим собственные значения матрицы 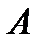 . Далее, неособенная матрица
. Далее, неособенная матрица  , полученная в методе Данилевского, используется при нахождении собственных векторов матрицы
, полученная в методе Данилевского, используется при нахождении собственных векторов матрицы 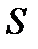 в методе Данилевского осуществляется последовательно с помощью
в методе Данилевского осуществляется последовательно с помощью  преобразований подобия, которые переводят строки матрицы
преобразований подобия, которые переводят строки матрицы 


