
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Локальная и глобальная ошибка одношагового метода решения задачи Коши. Задача для погрешности метода, устойчивость и сходимость.
При рассмотрении метода Эйлера было показано, что глобальная погрешность приближенного решения совпадает с локальной погрешностью метода – погрешностью аппроксимации дифференциальной задачи. При оценке локальной погрешности стандартной процедурой является следующая. Точное решение дифференциальной задачи подставляется в вычислительную схему, при этом учитывается, что его значение в некоторых узлах (узле) сетки уже известно (из начальных условий либо предыдущих вычислений), а значение решения в других узлах (узле) может быть выражено отрезком степенного ряда, используя исходное дифференциальное уравнение для нахождения соответствующих производных функции. Зная смысл погрешности аппроксимации задачи несложно понять, как взаимосвязана погрешность приближенного решения с погрешностью аппроксимации задачи (локальной ошибкой метода). Общая схема рассуждений такова. Мы имеем некоторый одношаговый численный метод, в котором приближенное решение в каждом новом узле сетки вычисляется с использованием некоторой функции F дискретных аргументов и параметра Если подстановка точного решения дифференциальной задачи в уравнение (1) приводит к тождеству то говорят, что схема (1) аппроксимирует исходное уравнение (0) с порядном Таким образом, происхождение погрешности численного метода можно интерпретировать либо как возмущение исходной дифференциальной задачи, обусловленное появлением в правой части уравнения (2) дополнительного малого слагаемого Анализ погрешности численной схемы ведется на основе уравнения для погрешности
Из ограниченности величины
Заметим, что совпадение локальной и глобальной ошибки одношаговых численных методов следует понимать только в смысле совпадения порядка малости данных величин. В силу этого, если некоторая стандартная программа, реализующая метод Рунге-Кутты, содержит среди входных параметров значение локальной погрешности для оценки требуемых шагов сетки при численном интегрировании задачи, не следует думать, что приближенное решение будет получено именно с такой точностью на произвольном отрезке численного интегрирования. При моделировании длительной динамики решения истинная (глобальная) погрешность приближенного решения может испытывать экспоненциальный рост и существенно отличаться от локальной погрешности. Чтобы убедиться в удовлетворительной точности решения в большинстве случаем достаточно сравнить приближенные решения, полученные на сетках с шагами При оценке погрешности метода Эйлера и методов Рунге-Кутты мы неявно полагали, что сами вычисления производятся точно. На практике, вообще говоря, это не так, поскольку реализация арифметических операций с действительными числами, имеющими компьютерное представление на конечной разрядной сетке, неизбежно ведет к округлению как самих действительных чисел, так результатов арифметических операций с ними. В силу этого, наряду с погрешностью аппроксимации дифференциальной задачи, приближенное решение будет содержать также ошибку, связанную с погрешностями представления и операций с действительными числами. Таким образом, погрешность приближенного решения дифференциальной задачи будет состоять из погрешности дискретизации задачи и вычислительной ошибки. Идентифицировать вычислительную погрешность численной схемы и оценить ее величину, для методов, обладающих сходимостью при
При численном решении задачи Коши обычно предпочтение отдают одношаговым методам, которые обладают устойчивостью вычислений, возможностью легко менять шаг сетки и отсутствием предварительного построения начала таблицы.
3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм Для оценки погрешности (разности векторов точного и приближенного решений) используются различные нормы линейного векторного пространства. Напомним, что нормой вектора 1. 2. 3. Векторные нормы, получившие наиболее широкое распространение в численном анализе:
Т.к. для матриц определена операция умножения, то естественно добавить требовавание Матричная норма называется согласованной, если Определение. Норма матрицы В случае квадратных матриц из определения подчиненной матричной нормы следует ее согласованность, мультипликативность и минимальность среди всех возможных согласованных норм. Подчиненные матричные нормы для приведенных выше основных векторных норм вычисляются следующим образом.
Выбор конкретной нормы для получения оценок приближенного решения определяется в основном целью исследований и спецификой задачи. При этом следует иметь в виду, что нормы конечномерного линейного векторного пространства эквивалентны с точностью до постоянного множителя.
Норма Например, для норм
|
|||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.138.230 (0.011 с.) |
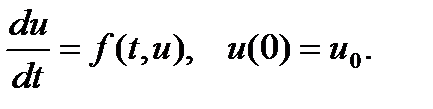 (0)
(0)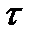 :
: 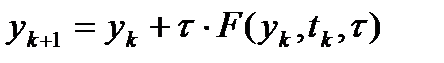 (1)
(1)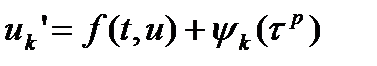 ,
, 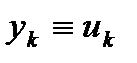 (2) или
(2) или 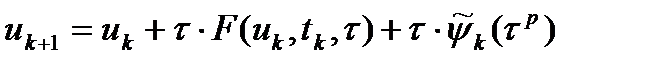 (3)
(3)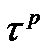 .
.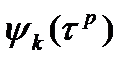 , либо как отбрасывание такого рода слагаемых при переходе от точного выражения для решения (3) к приближенной схеме (1).
, либо как отбрасывание такого рода слагаемых при переходе от точного выражения для решения (3) к приближенной схеме (1).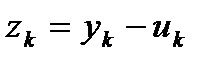 , которое получается при вычитании (3) из (1):
, которое получается при вычитании (3) из (1):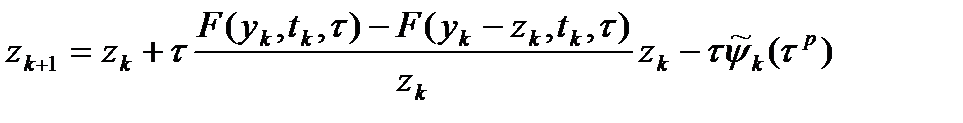 (4)
(4)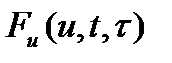 в окрестности точного решения следует, что, согласно (4), ошибка приближенного решения на каждом шаге метода может возрастать на величину порядка
в окрестности точного решения следует, что, согласно (4), ошибка приближенного решения на каждом шаге метода может возрастать на величину порядка 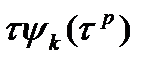 . Учитывая, что количество шагов сетки на конечном отрезке по t есть величина порядка
. Учитывая, что количество шагов сетки на конечном отрезке по t есть величина порядка 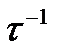 , то в худшем случае суммирования погрешностей на каждом шаге, максимальная ошибка на всем интервале будет величиной порядка
, то в худшем случае суммирования погрешностей на каждом шаге, максимальная ошибка на всем интервале будет величиной порядка  , т.е. иметь тот же порядок, что и погрешность аппроксимации метода.
, т.е. иметь тот же порядок, что и погрешность аппроксимации метода.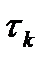 и
и 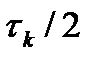 .
. 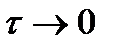 , можно следующим образом. Выполнить расчеты на последовательности сеток с шагами
, можно следующим образом. Выполнить расчеты на последовательности сеток с шагами  . Далее, следует оценить погрешность приближенного решения на каждой сетке, используя точное решение задачи (заметим, что понятие точного решения при оценках вычислительной погрешности весьма условно, поскольку вычисленное "точное" решение также будет содержать некоторую вычислительную погрешность). При уменьшении шага оказывается, что, начиная с некоторой достаточно малой величины
. Далее, следует оценить погрешность приближенного решения на каждой сетке, используя точное решение задачи (заметим, что понятие точного решения при оценках вычислительной погрешности весьма условно, поскольку вычисленное "точное" решение также будет содержать некоторую вычислительную погрешность). При уменьшении шага оказывается, что, начиная с некоторой достаточно малой величины 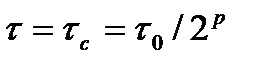 , его дальнейшее уменьшение не приводит к уменьшению погрешности решения, или даже напротив – ведет к возрастанию ошибки. Это является следствием того, что ошибка, обусловленная погрешностью метода, при
, его дальнейшее уменьшение не приводит к уменьшению погрешности решения, или даже напротив – ведет к возрастанию ошибки. Это является следствием того, что ошибка, обусловленная погрешностью метода, при  уменьшилась настолько, что стала ниже вычислительной погрешности. С уменьшением шага сетки на конечном интервале численного интегрирования задачи растет число шагов, требуемое для покрытия данного интервала. Как следствие, растет общий объем вычислений с округлениями, дающими вклад в вычислительную погрешность. Накопление вычислительной погрешности, хотя это и не обязательно, может приводить к некоторому росту общей ошибки решения при
уменьшилась настолько, что стала ниже вычислительной погрешности. С уменьшением шага сетки на конечном интервале численного интегрирования задачи растет число шагов, требуемое для покрытия данного интервала. Как следствие, растет общий объем вычислений с округлениями, дающими вклад в вычислительную погрешность. Накопление вычислительной погрешности, хотя это и не обязательно, может приводить к некоторому росту общей ошибки решения при  .
.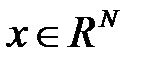 называется произвольный линейный положительно определенный функционал
называется произвольный линейный положительно определенный функционал 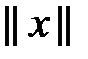 , который
, который 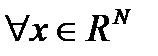 удовлетворяет трем аксиомам:
удовлетворяет трем аксиомам: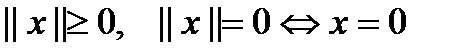 – положительная определенность;
– положительная определенность;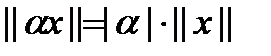 ,
, 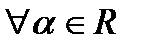 – линейность при умножении на скаляр;
– линейность при умножении на скаляр;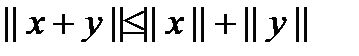 – неравенство треугольника.
– неравенство треугольника.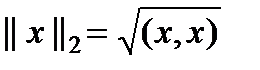 – Евклидова норма (при соответ-м определении скалярного произведения);
– Евклидова норма (при соответ-м определении скалярного произведения);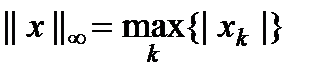 – максимальная норма;
– максимальная норма;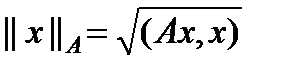 – энергетическая норма, порожденная положительно определенным самосопряженным оператором
– энергетическая норма, порожденная положительно определенным самосопряженным оператором 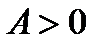 .
.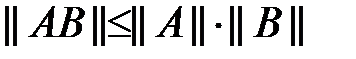 – аксиома мультипликативности матричной нормы.
– аксиома мультипликативности матричной нормы.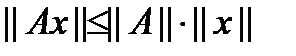 (вектор
(вектор 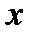 в данном случае может трактоваться как матрица, имеющая размерность
в данном случае может трактоваться как матрица, имеющая размерность 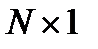 ). Для получения не улучшаемых оценок произведения матрицы на вектор используют нормы матриц, подчиненные соответствующим векторным нормам.
). Для получения не улучшаемых оценок произведения матрицы на вектор используют нормы матриц, подчиненные соответствующим векторным нормам.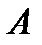 , подчиненная векторной норме
, подчиненная векторной норме 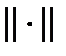 , определяется числом
, определяется числом 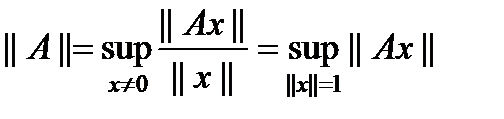 (1)
(1) – матричная норма, подчиненная векторной Евклидовой норме, равна максимальному сингулярному числу матрицы. Сингулярные числа матрицы вычисляются как корень квадратный из совпадающих собственных значений матриц
– матричная норма, подчиненная векторной Евклидовой норме, равна максимальному сингулярному числу матрицы. Сингулярные числа матрицы вычисляются как корень квадратный из совпадающих собственных значений матриц 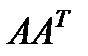 и
и 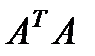 . Для симметричной, положительно определенной матрицы сингулярные числа совпадают со спектром собственных значений данной матрицы.
. Для симметричной, положительно определенной матрицы сингулярные числа совпадают со спектром собственных значений данной матрицы.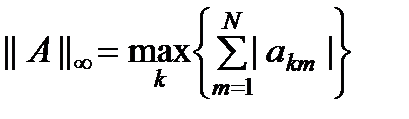 . В качестве данной нормы выступает максимальное значение суммы абсолютных величин элементов строк матрицы.
. В качестве данной нормы выступает максимальное значение суммы абсолютных величин элементов строк матрицы.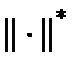 эквивалентна норме
эквивалентна норме 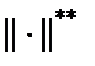 если для любого элемента
если для любого элемента  (вектора или матрицы) найдутся такие постоянные
(вектора или матрицы) найдутся такие постоянные  и
и 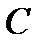 , что выполняется неравенства
, что выполняется неравенства 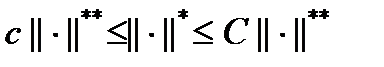 .
. 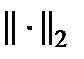 и
и 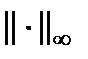 имеют место оценки
имеют место оценки 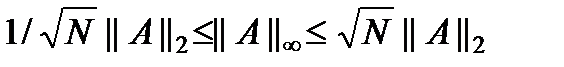 ,
, 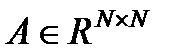 .
.


