
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение производной высокого порядка.⇐ ПредыдущаяСтр 11 из 11
Если разложить функцию в ряд и рассмотреть слагаемое со степенью n, то можно сравнить его с теоретически полученным видом Пример. Найти
Здесь нам нужен только коэффициент при степени 10.
Нахождение определённого интеграла. Если функция требует больших трудоёмких подстановок, или многократного интегрирования по частям, можно разложить функцию в ряд, состоящий из степенных функций, и приближённо вычислить. Пример. Приближённо найти интеграл
Как видим, даже 2-е слагаемое можно было не рассматривать, т.к. оно меньше, чем
Решение дифференциальных уравнений. Можно представить неизвестную функцию Пример 1.
Из равенства
В этом случае все коэффициенты можно последовательно выразить через Тогда
Пример 2. Решить дифференциальное уравнение Решение.
Подставим в уравнение.
... ... Из этих двух групп равенств можно все чётные коэффициенты выразить через
аналогично, Тогда
Впрочем, константы можно переобозначить через Ответ.
Ряды Лорана Ряд вида
Совокупность слагаемых с нулевой и положительной степенью называется его правильной частью, а отрицательных - главной частью.
Теорема 1. Область сходимости ряда Лорана есть кольцо вида Доказательство. Распишем по отдельности на главную и правильную часть: 1. Для правильной части верна теорема Абеля, ведь это обычный степенной ряд. Правильная часть абсолютно сходится в некотором круге 2. Рассмотрим главную часть ряда Лорана Сделаем в ней замену с целью представить через положительные степени и применить теорему Абеля. Итак, область сходимости есть
Крайние случаи: Если Если
Пример. Найти кольцо сходимости ряда Лорана: Решение. Найдём отдельно по радикальному признаку Коши область сходимости правильной и главной части. 1. Для 2. Для Ответ. Кольцо сходимости:
Теорема 2. (о разложении в ряд Лорана). Пусть
Следствие. Коэффициент
Разложение в ряд Лорана с помощью геометрической прогрессии. Пример. Разложить функцию а) в ряд Лорана в кольце б) во внешней области в) в ряд Тейлора в круге Во-первых, если центр кольца 0, а точки разрыва Чертёж:
Разложим на простейшие дроби. Это действие необходимо в любом случае, независимо от того, в каком множестве надо получать разложение в ряд.
1) Для разложения в ряд Лорана в кольце, надо вынести за скобку иногда константу, а иногда Из условия
теперь в каждом случае получено выражение вида
2) Теперь разложим в ряд во внешней области, которую, впрочем, можно также считать кольцом типа
3) Если требуется разложить в ряд в круге, то это получится ряд Тейлора, там наоборот, в обеих дробях надо выносить константу, чтобы было
Ряды Фурье Скалярное произведение функций. Вспомним скалярное произведение векторов Для функций можно построить обобщение. Если заданы 2 функции Итак, определим скалярное произведение пары функций на интервале Можно считать, что это верно и на отрезке Пример. Найти скалярное произведение Решение.
Свойства скалярного произведения, которые легко следуют из свойств линейности интеграла:
Вспомним, что для векторов есть понятие модуля,
Очевидно, что этот квадратный корень существует, ведь Ортогональные функции. Две функции называются ортогональными на интервале Здесь нет такого простого геометрического смысла, как в случае перпендикулярных векторов, для функций ортогональность значит, что произведение функций где-то больше, а где-то меньше нуля так, чтобы эти части компенсировались и уничтожились при интегрировании. Пример. Доказать, что функции
Пример. Доказать, что функции
Замечание. Если одна из функций в произведении тождественно равна 0, то интеграл очевидно, равен 0. Поэтому тождественный 0 это ортогональная всем функция.
Ортогональные системы. Если любая пара функций в системе ортогональна, то система называется ортогональной.
ЛЕКЦИЯ № 11. 17.11.2020
|
||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.9.236 (0.069 с.) |
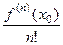 и отсюда извлекается информация о значении
и отсюда извлекается информация о значении 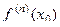 , причём не требуется вычислять все производные включительно до n порядка, а сразу получаем значение n-й производной в точке. Ведь бывает так, что функция содержит произведение, и там число слагаемых удваивается на каждом шаге, и их уже 1024 для 10-й производной.
, причём не требуется вычислять все производные включительно до n порядка, а сразу получаем значение n-й производной в точке. Ведь бывает так, что функция содержит произведение, и там число слагаемых удваивается на каждом шаге, и их уже 1024 для 10-й производной. 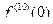 для
для 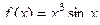 .
.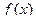 =
= 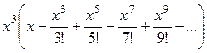 =
= 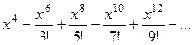
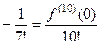
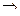
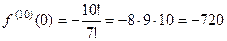 . Ответ.
. Ответ. 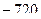 .
.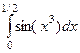 с точностью
с точностью 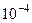 .
.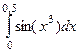 =
= 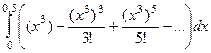 =
= 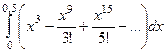 =
= 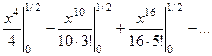 =
=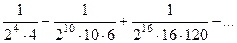 очевидно, здесь 3 и последующие слагаемые заведомо меньше
очевидно, здесь 3 и последующие слагаемые заведомо меньше 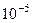 , и не повлияют на 4-й знак после запятой, поэтому приближённое значение
, и не повлияют на 4-й знак после запятой, поэтому приближённое значение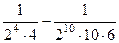 =
= 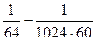
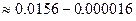
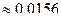 .
.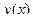 в виде степенного ряда
в виде степенного ряда 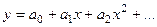 и подставить его в дифференциальное уравнение, тогда решение найдётся тоже в виде ряда, т.е. можно знать строение решения, его график и т.д. даже без аналитического выражения этой функции..
и подставить его в дифференциальное уравнение, тогда решение найдётся тоже в виде ряда, т.е. можно знать строение решения, его график и т.д. даже без аналитического выражения этой функции..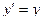 решить с помощью степенных рядов.
решить с помощью степенных рядов.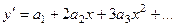
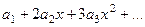 =
= 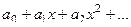 получаем:
получаем: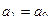 ,
, 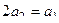 ,
, 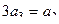 и так далее.
и так далее.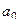 . А именно,
. А именно, 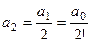 ,
, 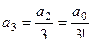 и т.д.
и т.д.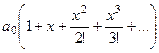 здесь видно, что в скобках получилось разложение экспоненты. Итак,
здесь видно, что в скобках получилось разложение экспоненты. Итак, 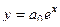 . Эту единственную константу можно переобозначить
. Эту единственную константу можно переобозначить 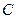 и получится знакомый вид общего решения такого уравнения:
и получится знакомый вид общего решения такого уравнения: 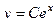 .
.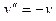 с помощью степенных рядов.
с помощью степенных рядов.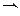
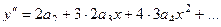
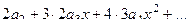 =
= 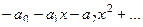 тогда:
тогда: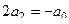 ,
, 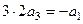 ,
, 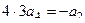 ,
, 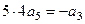 ,
, 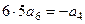 ,
, 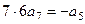 ,
, 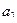 .
. 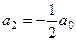 ,
, 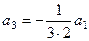
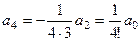 ,
, 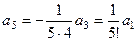 ,...
,...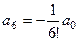 ,
, 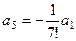 ,
, 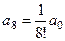 ,
, 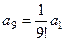 ,...
,...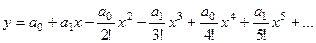 =
=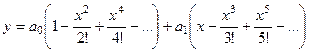 =
= 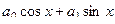 .
.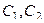 и записать решение в привычном виде
и записать решение в привычном виде 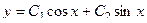 .
.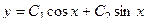 .
.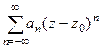 , то есть содержащий как положительные, так и отрицательные целые степени, называется рядом Лорана.
, то есть содержащий как положительные, так и отрицательные целые степени, называется рядом Лорана.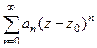 правильная часть,
правильная часть, 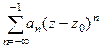 главная часть, её также можно переписать в виде:
главная часть, её также можно переписать в виде: 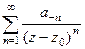 .
.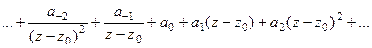
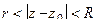 .
.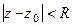 .
. . тогда для новой переменной
. тогда для новой переменной 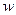 ряд принимает такой вид:
ряд принимает такой вид: 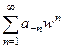 . Это степенной ряд, его круг сходимости с центром в 0. То есть,
. Это степенной ряд, его круг сходимости с центром в 0. То есть, 
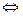
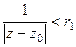
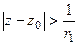 , обозначим
, обозначим 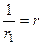 , вот и получили
, вот и получили 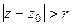 .
.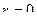 : круг с выколотой точкой
: круг с выколотой точкой 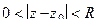 . Это происходит, если в главной части лишь конечное количество слагаемых. Их значение не существует только в самой точке
. Это происходит, если в главной части лишь конечное количество слагаемых. Их значение не существует только в самой точке 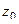 , а в любой точке из её окрестности - существует. Поэтому из области сходимости исключается лишь одна точка.
, а в любой точке из её окрестности - существует. Поэтому из области сходимости исключается лишь одна точка. : внешняя часть некоторого круга
: внешняя часть некоторого круга 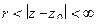 .
. 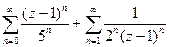 .
.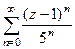 получается
получается 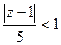 , т.е.
, т.е. 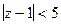

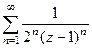 получается
получается 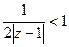 , т.е.
, т.е. 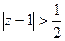 .
.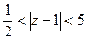 .
. является аналитической в некотором кольце с центром
является аналитической в некотором кольце с центром 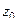 , тогда она представима в виде ряда
, тогда она представима в виде ряда 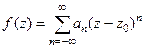 , причём
, причём 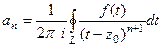 .
. 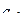 ряда Лорана равен вычету функции в точке
ряда Лорана равен вычету функции в точке 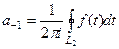 .
.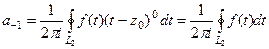 .
.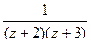 :
: 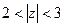
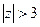
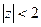 .
. и
и  , то есть 3 области:
, то есть 3 области: 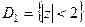 ,
, 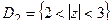 ,
, 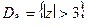 .
.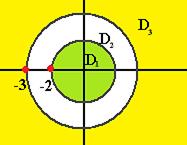
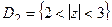 кольцо, расположенное между двумя точками разрыва, так, чтобы ни одна из них не была внутри кольца.
кольцо, расположенное между двумя точками разрыва, так, чтобы ни одна из них не была внутри кольца.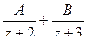 =
= 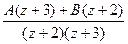
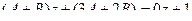
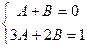
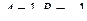
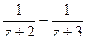 .
. , чтобы всегда получалось что-то меньшее 1.
, чтобы всегда получалось что-то меньшее 1.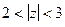 следует
следует 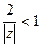 и
и 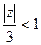 , то есть в знаменателе можно получать
, то есть в знаменателе можно получать 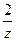 и
и 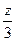 , но нельзя
, но нельзя 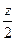 и
и 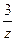 .
.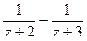 =
= 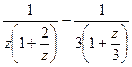 =
= 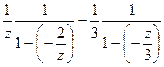
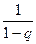 которое и является суммой геометрической прогрессии, и его можно превратить в бесконечную сумму по формуле
которое и является суммой геометрической прогрессии, и его можно превратить в бесконечную сумму по формуле 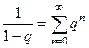 .
.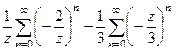 =
=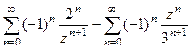 =
= 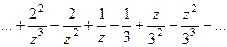
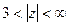 . Здесь
. Здесь 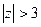 причём автоматически выполнено также и
причём автоматически выполнено также и 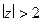 , т.е. надо получать в знаменателях выражения
, т.е. надо получать в знаменателях выражения 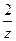 и
и 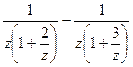 =
= 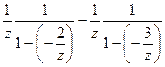 =
=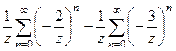 в данном случае их можно и объединить, т.к. в каждом слагаемом есть одинаковые степени.
в данном случае их можно и объединить, т.к. в каждом слагаемом есть одинаковые степени.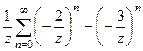 =
= 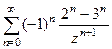 . В этом ряде Лорана есть только главная часть.
. В этом ряде Лорана есть только главная часть.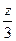 и
и 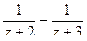 =
= 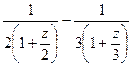 =
= 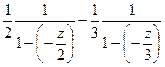 =
=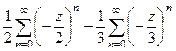 =
= 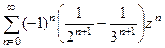 .
.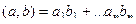 .
.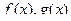 , то очевидно, их можно умножить в каждой точке. Затем все эти произведения надо проинтегрировать, так как точек на интервале бесконечное количество. Получается как бы бесконечное количество координат.
, то очевидно, их можно умножить в каждой точке. Затем все эти произведения надо проинтегрировать, так как точек на интервале бесконечное количество. Получается как бы бесконечное количество координат.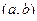 по формуле:
по формуле: 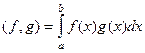 .
.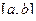 , ведь две граничные точки не влияют на величину интеграла.
, ведь две граничные точки не влияют на величину интеграла.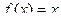 и
и 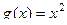 на интервале (0,1).
на интервале (0,1).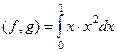 =
= 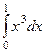 =
= 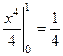 .
.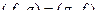
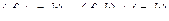 ,
, 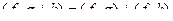
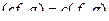 ,
, 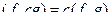
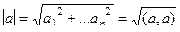 . Аналогичное понятие для функций называется нормой функции:
. Аналогичное понятие для функций называется нормой функции: 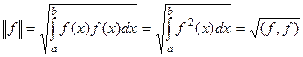 .
.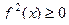 , а значит и
, а значит и 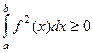 .
.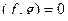 , то есть
, то есть 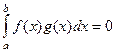 .
.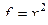 ,
, 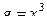 ортогональны на интервале
ортогональны на интервале 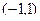 .
.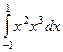 =
= 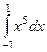 =
= 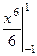 =
= 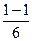 = 0.
= 0.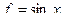 ,
, 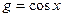 ортогональны на интервале
ортогональны на интервале 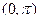 .
.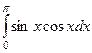 =
= 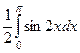 =
= 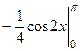 =
= 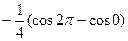 = 0.
= 0.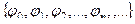 ортогональна, если
ортогональна, если 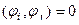 для любых
для любых 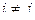 .
.


