
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды Тейлора и их приложения.
В конце прошлого параграфа изучали степенные ряды и находили суммы S(x). Обратная задача: дана функция, надо представить её в виде степенного ряда, т.е. «разложить в степенной ряд». Ряд
Докажем с помощью интегральной формулы Коши, что верно разложение в ряд Тейлора не только для функций действительного переменного (1 семестр), но и для комплексных функций. Теорема (о разложении в ряд Тейлора). Пусть Тогда она представима в виде степенного ряда:
Доказательство. Рассмотрим окрестность точки
Можно записать интегральную формулу Коши для точки Изучим дробь
Тогда
Оставим внутри знака интеграла только те множители, которые зависят от Тогда Что и требовалось доказать: получилось разложение в ряд Тейлора с коэффициентами
Метод определения круга сходимости. Если дана функция, и требуется разложить в ряд Тейлора по степеням
Пусть Пример. Разложить
В точке 0 n-я производная равна n! Тогда Но не обязательно так искать все производные и устанавливать закономерность при их вычислении. Иногда количество слагаемых при дифференцировании экспоненциально возрастает (если было произведение) на каждом шаге в 2 раза и равно Итак,
Рассмотрим разные модификации для других случаев.
Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: Сумма вместо разности вовсе не является препятствием к тому, чтобы использовать прогрессию, запишем
Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: Решение. Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии Здесь мы сначала определим круг сходимости. От точки 1 до точки разрыва Отделим разность
ЛЕКЦИЯ № 10. 3.11.2020 Приложения рядов Тейлора.
Вспомним некоторые разложения известных функций в ряды Тейлора.
Приближённые вычисления.
Значения функции в точке можно приближённо вычислять с помощью разложения в ряд Тейлора, более того, во всех калькуляторах и компьютерах именно так и запрограммировано. Каждая функция там задана просто в виде набора коэффициентов ряда, и при обращении к функции именно это и вычисляется автоматически, с той точностью, с которой позволяет разрядная сетка калькулятора. Так, вычислим
|
||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.168 (0.015 с.) |
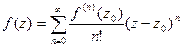 - разложение функции
- разложение функции 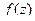 в степенной ряд в окрестности точки
в степенной ряд в окрестности точки  , он называется рядом Тейлора этой функции. Соответственно, для действительных функций,
, он называется рядом Тейлора этой функции. Соответственно, для действительных функций, .
.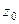 .
.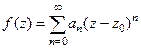 , где
, где 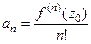 .
. , лежащую внутри неё. Пусть граница окрестности - кривая
, лежащую внутри неё. Пусть граница окрестности - кривая 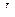 , а точку на ней обозначим
, а точку на ней обозначим  .
.
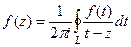 (здесь
(здесь 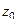 ).
).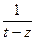 подробнее. Можно прибавить и отнять
подробнее. Можно прибавить и отнять 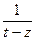 =
= 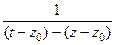 а дальше преобразовать к виду суммы геометрической прогрессии, чтоб воспользоваться тем фактом, что
а дальше преобразовать к виду суммы геометрической прогрессии, чтоб воспользоваться тем фактом, что  . Причём выносить за скобку в знаменателе надо именно такой из двух блоков, чтобы получилось 1 и нечто меньшее по модулю, чем 1. Учитывая, что
. Причём выносить за скобку в знаменателе надо именно такой из двух блоков, чтобы получилось 1 и нечто меньшее по модулю, чем 1. Учитывая, что  , т.е.
, т.е. 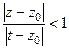
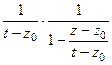 =
= 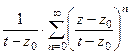 =
=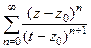 . Подставим это выражение в интегральную формулу Коши вместо
. Подставим это выражение в интегральную формулу Коши вместо 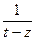 . Тогда
. Тогда 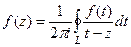 =
= 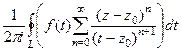 =
= 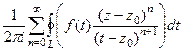 .
.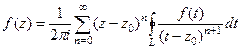 но оставшийся внутри суммы интеграл можно преобразовать по обобщённой интегральной формуле Коши из теоремы 3, ведь если
но оставшийся внутри суммы интеграл можно преобразовать по обобщённой интегральной формуле Коши из теоремы 3, ведь если 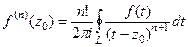 то
то 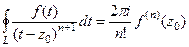 .
.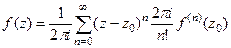 =
= 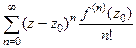 .
. .
.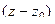 то радиус круга сходимости определяется расстоянием от центра, а именно точки
то радиус круга сходимости определяется расстоянием от центра, а именно точки 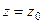 до ближайшей точки разрыва.
до ближайшей точки разрыва.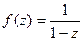 . Если надо разложить её в ряд вида
. Если надо разложить её в ряд вида 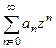 , то центр
, то центр 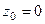 , а ближайшая точка, где ряд точно расходится, это точка разрыва
, а ближайшая точка, где ряд точно расходится, это точка разрыва  . Тогда круг сходимости как раз и будет
. Тогда круг сходимости как раз и будет 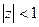 .
.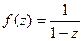 =
=  . Тогда:
. Тогда: 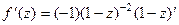 =
= 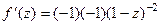 =
= 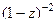 .
.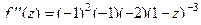 =
= 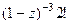
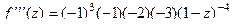 =
= 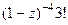 , и.т.д.
, и.т.д.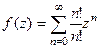 =
=  =
=  .
. , так что напрямую по формуле считать не всегда удобно. Второй способ - получать разложение сразу, используя геометрическую прогрессию. Применяем формулу суммы прогрессии
, так что напрямую по формуле считать не всегда удобно. Второй способ - получать разложение сразу, используя геометрическую прогрессию. Применяем формулу суммы прогрессии 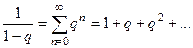 при этом желательно заранее вынести все множители из числителя за пределы дроби, чтобы «очистить» числитель до 1, этим самым мы обеспечиваем то, что можно пользоваться упрощённой формулой суммы прогрессии
при этом желательно заранее вынести все множители из числителя за пределы дроби, чтобы «очистить» числитель до 1, этим самым мы обеспечиваем то, что можно пользоваться упрощённой формулой суммы прогрессии 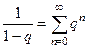 , где
, где 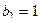 .
.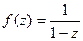 . Заметим, что при
. Заметим, что при  эта функция может рассматриваться как сумма прогрессии (т.е. уже свёрутая по формуле суммы). Здесь знаменатель прогрессии
эта функция может рассматриваться как сумма прогрессии (т.е. уже свёрутая по формуле суммы). Здесь знаменатель прогрессии 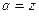 . Тогда
. Тогда  как видим, то же самое и получили.
как видим, то же самое и получили.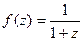 по степеням
по степеням 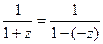 тогда
тогда 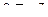 и
и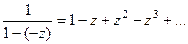 если в знаменателе сумма, получается знакочередующийся ряд.
если в знаменателе сумма, получается знакочередующийся ряд.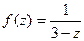 по степеням
по степеням 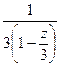 =
= 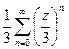 =
= 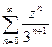 .
.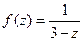 по степеням
по степеням  , то есть в круге с центром в точке 1.
, то есть в круге с центром в точке 1. равно 2, так что разложение в ряд возможно в круге
равно 2, так что разложение в ряд возможно в круге  .
. искусственным путём, т.е. прибавим и отнимем 1.
искусственным путём, т.е. прибавим и отнимем 1. . А теперь далее не раскрываем блок
. А теперь далее не раскрываем блок  вплоть до ответа, то есть эта скобка так и будет как единое целое.
вплоть до ответа, то есть эта скобка так и будет как единое целое.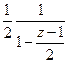 =
= 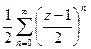 =
= 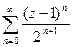 . Заметим, что при этом знаменатель прогрессии
. Заметим, что при этом знаменатель прогрессии 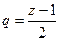 , он должен быть меньше 1 по модулю, но так и есть, ведь круг сходимости
, он должен быть меньше 1 по модулю, но так и есть, ведь круг сходимости 

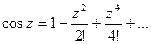
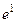 . Известно, что
. Известно, что 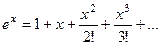 . Тогда
. Тогда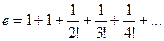 =
=  Так, для первых шагов сразу получаем значение 2,5 затем прибавляется
Так, для первых шагов сразу получаем значение 2,5 затем прибавляется  и стало
и стало  а затем
а затем 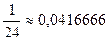 станет
станет 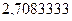 и так с каждым шагом всё ближе к
и так с каждым шагом всё ближе к 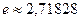 .
.


