
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеризация бесконечно-удалённой точки.
Когда мы вычисляем предел в точке Существует геометрическая модель, в которой бесконечно-удалённая точка присутствует на равных с другими точками. Поместим сферу над плоскостью в начало координат. Если от верхней точки S провести любую наклонную прямую, то она 1 раз пересечётся со сферой и 1 раз с плоскостью. Таким образом, каждой точке комплексной плоскости можно однозначно поставить в соответствие точку на сфере. При этом единственная точка, для которой нет образа на плоскости - это точка S. Она соответствует горизонтальной касательной, и можно поставить ей в соответствие «бесконечно удалённую точку».
Если на плоскости точка устремится к
Классификация
Только в данном случае наоборот, полюс если степень m в числителе, а не в знаменателе. Например, для В задачах можно делать замену Пример. Определить тип точки Решение. Сделаем замену Попутно заметим, что Для точки Пример. Определить тип точки Решение. Сделаем замену Пример. Определить тип точки Решение. Сделаем замену Если устремить
Вывод: предел в точке
Вычеты. Определение. Пусть
Формулы вычисления вычетов. Если Если
Они напрямую следуют из обычной и обобщённой интегральных формул Коши. Кстати, первая формула - частный случай второй при Пример. Найти вычет Решение. Здесь точка
Пример. Найти вычет Решение. Здесь точка
Пример *. Найти вычет Решение. Здесь точка
Основная теорема о вычетах. Если
Доказательство. По интегральной теореме Коши, интеграл по контуру Тогда
Вот и получается, что интеграл равен такой величине: Определение вычета в
Когда мы рассматривали конечную точку
Теорема (следствие из основной теоремы о вычетах). Если (Сумма вычетов во всех конечных особых точках + вычет в бесконечности равно 0). Доказательство. Если в плоскости конечное количество особых точек, то среди них есть самая далёкая от начала координат. Тогда их все можно включить в круг некоторого радиуса. Ограничим все n особых точек замкнутым контуром По определению вычета в а по прошлой теореме, Получается, что вычет в Чертёж.
Пример. Найти Решение. Заметим, что в знаменателе только
ЛЕКЦИЯ № 7. 14.10.2020 Приложения вычетов
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.194 (0.023 с.) |
 , он может быть конечным, бесконечным либо не существовать. Аналогично этому, подобные ситуации могут быть и при вычислении предела
, он может быть конечным, бесконечным либо не существовать. Аналогично этому, подобные ситуации могут быть и при вычислении предела 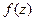 при
при  . Бесконечность не является точкой в плоскости, тем не менее, тип такого объекта как «бесконечно-удалённая точка» можно тоже классифицировать как и типы особых точек, с помощью предела.
. Бесконечность не является точкой в плоскости, тем не менее, тип такого объекта как «бесконечно-удалённая точка» можно тоже классифицировать как и типы особых точек, с помощью предела.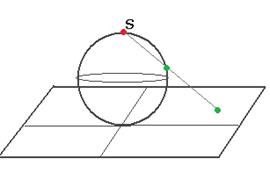
 , то её образ на сфере устремится к точке S.
, то её образ на сфере устремится к точке S. :
: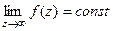

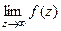 не существует
не существует
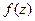 =
= 
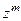
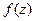 =
= 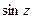
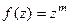 полюс порядка m.
полюс порядка m.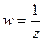 и таким образом сводить изучение
и таким образом сводить изучение 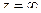 к изучению поведения функции в точке
к изучению поведения функции в точке 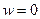 .
. .
. , т.е. После этого функция изменит вид так:
, т.е. После этого функция изменит вид так: 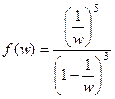 =
=  =
= 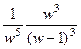 .
. а значит и
а значит и  - полюс 3-го порядка.
- полюс 3-го порядка. , соответствующей
, соответствующей  , видим нуль 3-го порядка в числителе и 5-го порядка в знаменателе. Сократив дробь, можно получить
, видим нуль 3-го порядка в числителе и 5-го порядка в знаменателе. Сократив дробь, можно получить 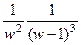 . Тогда видно, что
. Тогда видно, что  полюс 2-го порядка, а значит,
полюс 2-го порядка, а значит, 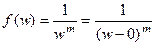 , то есть
, то есть 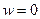 полюс порядка m, значит
полюс порядка m, значит  .
.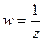 , т.е. После этого
, т.е. После этого 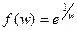 .
. к 0 со стороны положительной полуоси, то получается
к 0 со стороны положительной полуоси, то получается  . Если со стороны отрицательной полуоси, то
. Если со стороны отрицательной полуоси, то  . А если со стороны мнимой оси, то предел вообще не существует: при
. А если со стороны мнимой оси, то предел вообще не существует: при  ,
,  , и при этом
, и при этом 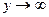 , при этом
, при этом 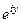 =
= 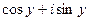 , т.е. при
, т.е. при  не существует предел ни действительной, ни мнимой части. Итак, приближаясь к (0,0) на плоскости с разных сторон, получаем разные результаты, а при приближении по некоторым траекториям предел даже не существует.
не существует предел ни действительной, ни мнимой части. Итак, приближаясь к (0,0) на плоскости с разных сторон, получаем разные результаты, а при приближении по некоторым траекториям предел даже не существует.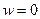 не существует,
не существует,  замкнутый контур, внутри него точка
замкнутый контур, внутри него точка 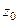 , на самом контуре и внутри него нет особых точек, кроме
, на самом контуре и внутри него нет особых точек, кроме 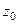 . Тогда интеграл
. Тогда интеграл 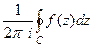 называется вычетом функции
называется вычетом функции 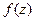 в точке
в точке 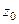 и обозначается
и обозначается  .
.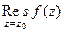 =
= 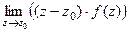 .
.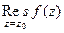 =
= 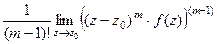 .
. .
.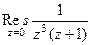 .
.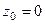 полюс порядка 3, конкретизируем формулу для этого порядка и этой точки:
полюс порядка 3, конкретизируем формулу для этого порядка и этой точки: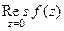 =
= 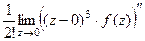 . Итак,
. Итак, 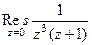 =
=  =
= 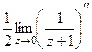 =
= 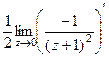 =
= 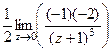 =
=  = 1.
= 1. .
. полюс 1 порядка. Поэтому
полюс 1 порядка. Поэтому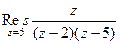 =
= 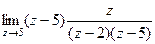 =
= 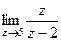 =
= 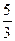 .
.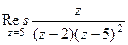 .
.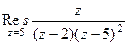 =
= 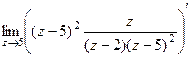 =
=  =
=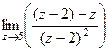 =
=  =
= 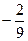 .
. является аналитической на некотором замкнутом контуре
является аналитической на некотором замкнутом контуре 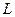 и в области внутри него, за исключением конечного количества изолированных особых точек, то
и в области внутри него, за исключением конечного количества изолированных особых точек, то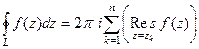 .
.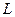 равен сумме интегралов по n контурам внутри него.
равен сумме интегралов по n контурам внутри него.  . Но каждое слагаемое в этой сумме - интеграл по контуру вокруг одной особой точки, делённый на
. Но каждое слагаемое в этой сумме - интеграл по контуру вокруг одной особой точки, делённый на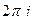 , а по определению это и есть вычет в данной точке
, а по определению это и есть вычет в данной точке  .
.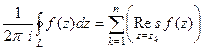
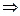
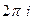 умножить на сумму вычетов.
умножить на сумму вычетов. называется вычетом функции
называется вычетом функции 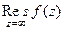 .
.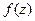 является аналитической во всей комплексной плоскости, за исключением конечного количества изолированных особых точек, то
является аналитической во всей комплексной плоскости, за исключением конечного количества изолированных особых точек, то 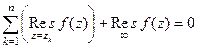 .
.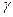 настолько большого радиуса
настолько большого радиуса 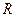 , чтобы все они лежали внутри круга
, чтобы все они лежали внутри круга  .
.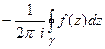 =
= 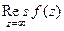 ,
,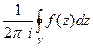 =
= 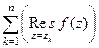 .
. .
. ,
, 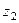 ,...
,... 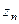 - особые точки.
- особые точки. 
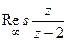 .
.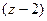 , т.е. эта функция имеет всего лишь одну конечную особую точку. Тогда:
, т.е. эта функция имеет всего лишь одну конечную особую точку. Тогда: =
= 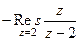 . То есть надо найти вычет в точке 2 и сменить знак.
. То есть надо найти вычет в точке 2 и сменить знак.  =
=  =
=  = 2. Поэтому
= 2. Поэтому 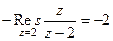 .
. 


