
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория функций комплексного переменного.Стр 1 из 11Следующая ⇒
Приходовский М.А. Математика - 3 семестр Курс лекций Учебное пособие Группы 519-1-2, 529, 539. Томск ТУСУР 2020 Оглавление по темам Глава 1. Теория функций комплексного переменного.....................3 § 1 Комплексные числа и действия над ними..........................................3 § 2 Функции комплексного переменного.................................................15 § 3. Дифференцирование комплексных функций....................................22 § 4. Интегрирование комплексных функций............................................29 § 5. Интегральная формула Коши............................................................36 § 6. Особые точки и вычеты.....................................................................42 Глава 2. Теория рядов............................................................................ 57 § 1. Числовые ряды..................................................................................... 57 § 2. Функциональные ряды........................................................................69 § 3. Степенные ряды...................................................................................71 § 4. Ряды Тейлора и их приложения.........................................................74 § 5. Ряды Лорана.............................................................................. § 6. Ряды Фурье................................................................................
Оглавление по номерам лекций Лекция № 1. 2.09.2020.........................................................3 Лекция № 2. 9.09.2020........................................................13 Лекция № 3. 16.09.2020......................................................21 Лекция № 4. 23.09.2020......................................................29 Лекция № 5. 30.09.2020......................................................36 Лекция № 6. 7.10.2020........................................................42 Лекция № 7. 14.10.2020......................................................52 Лекция № 8. 21.10.2020......................................................62 Лекция № 9. 28.10.2020......................................................71 Лекция № 10. 3.11.2020............................................ Лекция № 11. 17.11.2020......................................... Лекция № 12. 1.12.2020.......................................... Лекция № 13. 15.12.2020........................................ ЛЕКЦИЯ № 1. 2.09.2020 Глава 1. Теория функций комплексного переменного. Поиск корней многочлена с отрицательным дискриминантом. Пример. Найти корни уравнения Решение. Ответ. Кстати, как видно, получаются именно 2 взаимно сопряжённых корня. Проверка. Подставим, например,
Действительную и мнимую часть Докажем такие формулы: Доказательство. Сложим
Вычтем
Тригонометрическая форма комплексного числа. Введём величину
Абсцисса и ордината точки Выражение
Понятие модуля согласуется с известным понятием, применявшимся раньше для отрицательных чисел: модуль - расстояние по кратчайшей линии до начала координат. Для любой точки Так, число Число
Если вычислить синус и косинус, то снова перейдём к обычной, «алгебраической» форме числа:
Действительное число имеет аргумент 0 (если оно положительно) или
Угол может определяться разными способами, так, например, вместо угла
Докажем эту формулу.
используем известные тригонометрические формулы косинуса суммы и синуса суммы, и получим Примеры. Умножить
В тригонометрической форме: (используем представление чисел, которое сделали ранее).
Поделить
Формула Эйлера
Доказательство. Способ 1. Производная по
Способ 2. Вспомним разложение экспоненты по формуле Тейлора. Тогда вычислим Но ведь Тогда
Воспользуемся чётностью cos и нечётностью sin. Тогда:
Для любого числа
Для сопряжённого числа можно вычислить аналогично:
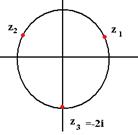
То есть, сопряжённое под знаком экспоненты приводит к сопряжённому результату. ЛЕКЦИЯ № 2. 9.09.2020 Корни порядка n. Корень порядка n вычисляется по такой формуле:
Доказательство. Если возведём в степень n, получим Добавка Пример. Найдите все значения корня Сначала представим комплексное число, которое находится под знаком корня, в тригонометрической форме. Точка расположена на мнимой оси выше начала координат, поэтому аргумент Теперь находим все 3 корня.
1) 2) 3) Чертёж:
Если к исходному углу добавить 120 градусов, то для куба этого числа добавится 360 градусов, и результат будет точно такой же. С этим фактом как раз и связано наличие лишнего слагаемого
Квадратных корней два, а именно
Доказательство. Рассмотрим для действительного числа 1) 2)
Неограниченность синуса и косинуса в комплексной плоскости. Пример. Вычислим:
Логарифм комплексного числа.
Обобщённый логарифм вводится с помощью формулы:
Доказательство. Проверим, совпадает ли
синус и косинус не зависят от прибавления угла, кратного А это уже и есть тригонометрическая форма комплексного числа. Итак, Если вычислять логарифм положительного действительного числа, то Пример. Вычислить Здесь Точки в комплексной плоскости: Ни одного значения на действительной оси нет, и здесь, по сравнению со значениями логарифма положительного числа, сдвиг на половину деления: одна точка ушла вверх с действительной оси, а другая ещё не достигла этой оси. Чертёж:
Здесь легко сделать и проверку: Пример. Вычислить
1) При фиксированном модуле исходного числа и увеличении его аргумента, эта последовательность точек плывёт вверх, при полном повороте на
2) При фиксированном аргументе исходного числа и увеличении его модуля, эта последовательность точек плывёт вправо, если исходная точка внутри единичной окружности то множество значений логарифма в левой полуплоскости, так как Динамическая анимация, показывающая поведение значений http://www.youtube.com/watch?v=LKFFn-TSLd0
Замечание. Единственная точка в комплексной плоскости, для которой не существует логарифма, это 0. Ведь в этом случае
Пример. Вычислить Решение. Представим
Для всякой функции
Пример. Разложить 1) Таким образом, Чтобы исследовать, куда переходят горизонтальные прямые, зафиксируем
Чтобы составить уравнение, взаимосвязывающее Аналогично, для какой-либо вертикальной прямой:
На чертеже зелёным цветом показаны горизонтальные прямые и их образы при отображении
Примечание. 4-мерный график можно было бы рассматривать таким образом: нужно как минимум 4 проекции на координатные пространства, а именно 0xyz, 0xzw, 0xyw, 0yzw. Либо можно рассмотреть 2 поверхности, построенные по функциям Пример. Разложить Используем то, что нашли ранее:
Здесь Пример. Разложить По формуле Эйлера:
ЛЕКЦИЯ № 3. 16.09.2020 Изучим подробнее линейное отображение, какие деформации плоскости происходят при действии линейной функции вида
Введём величину Тогда матрица линейного оператора имеет вид (домножим и поделим на квадратный корень):
Доказали, что линейное отображение
На этом чертеже показано, как изменяется плоскость при линейном отображении. Красным веделено горизонтальное направление, после отображения оно повёрнуто.
Замечание. Отображение
Достаточность. Пусть выполнены условия Коши-Римана Тогда производная матрица отображения Тогда, с точностью до бесконечно-малых, Тогда
Сложим эти 2 равенства, умножив при этом второе на
Теорема доказана.
Вывод. Итак, Пример. Проверить выполнение условий Коши-Римана для функции
2-е условие Коши-Римана). А сейчас мы рассмотрим функцию, для которой не выполнены условия Коши-Римана. Пример.
Решение. Способ 1. Производная как от единой функции
Способ 2. По компонентам
в точке Теорема 2.
Доказательство. Вспомним условие потенциальности поля Для векторного поля . Определение. Если функция дифференцируема и в самой точке Пример. Для функции Различие понятий аналитичности и дифференцируемости видно на другом примере. Пример.
1-е условие Коши-Римана выполняется только при
2-е условие Коши-Римана выполняется только при Таким образом, единственная точка в плоскости, где выполнены условия Коши-Римана, это (0,0). Но ни в одной точке из её окрестности они не выполняются, а только в одной изолированной точке
Теорема 3. Если функция является аналитической в некоторой области D, то для каждой из её частей (действительной и мнимой)
Доказательство. Запишем 2 условия Коши-Римана. Одно продифференцируем по переменной
Сложим теперь эти 2 равенства, но при этом смешанные производные 2 порядка от
Теперь снова запишем условия Коши-Римана, 1-е дифференцируем по
Теперь вычтем из 1-го равенства 2-е.
| Поделиться:
| |
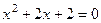 .
.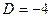 ,
, 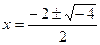 =
= 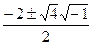 =
= 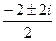 =
= 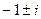 .
.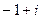 в уравнение.
в уравнение.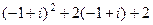 =
= 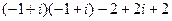 =
= 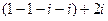 =
= 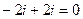 .
.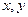 для числа
для числа 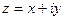 можно выразить через
можно выразить через 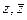 .
.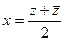 ,
, 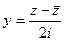
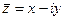 .
.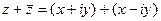 =
= 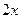 , тогда
, тогда 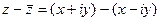 =
= 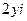 , тогда
, тогда 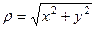 тогда
тогда 
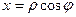 ,
, 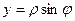 для некоторого
для некоторого 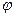 , ведь геометрически в этом случае
, ведь геометрически в этом случае 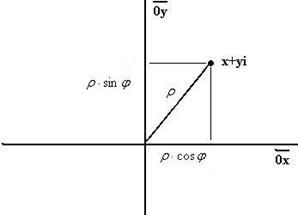
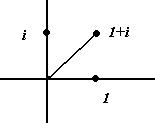
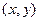 на плоскости это проекции на оси, они равны
на плоскости это проекции на оси, они равны 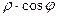 и
и 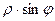 соответственно. Эти величины
соответственно. Эти величины 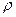 и
и 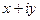 с помощью введённых выше величин
с помощью введённых выше величин 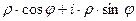 =
=  .
.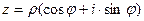 называется тригонометрической формой комплексного числа,
называется тригонометрической формой комплексного числа, 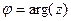
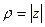 .
. . Для вычисления аргумента верна формула
. Для вычисления аргумента верна формула 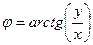 если точка в 4-й и 1-й четверти, либо
если точка в 4-й и 1-й четверти, либо 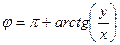 , если во 2-й и 3-й четверти.
, если во 2-й и 3-й четверти.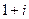 запишется в виде
запишется в виде 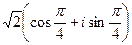 .
.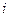 соответствует
соответствует 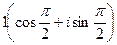 .
.
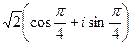 =
= 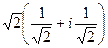 =
= 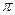 (если оно отрицательно).
(если оно отрицательно).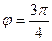 во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать
во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать 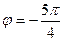 , и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток
, и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток 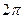 .
.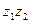 =
= 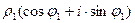
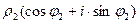 =
=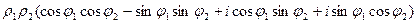 =
= .
. 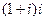 . Во-первых, это можно сделать и без триг.формы:
. Во-первых, это можно сделать и без триг.формы: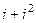 =
= 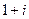 =
= 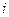 =
= 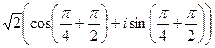 =
= 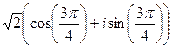 =
=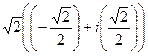 =
= 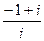 .
.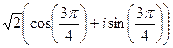 ,
, 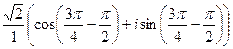 =
=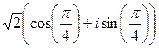 =
=  =
= 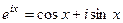
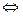
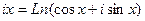
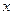 :
: 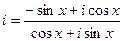 =
= 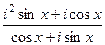 =
= 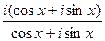 .
. 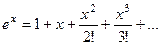
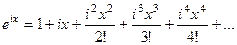
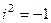 ,
, 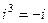 ,
, 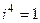 ,...
,...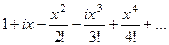 теперь соберём в отдельные слагаемые все части, где нет
теперь соберём в отдельные слагаемые все части, где нет 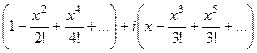 но ведь в 1 и 2 скобках - разложения
но ведь в 1 и 2 скобках - разложения 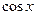 и
и 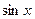 . Итак,
. Итак, 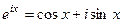 , что и требовалось доказать.
, что и требовалось доказать.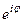 =
= 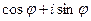 ,
, 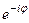 =
= 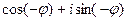 =...
=...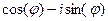 .
.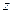 можно вычислить
можно вычислить  :
: 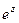 =
= 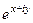 =
= 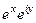 =
= 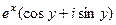 =
= 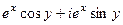 .
.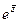 =
= 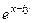 =
= 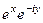 =
= 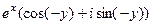 =
= 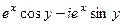 .
.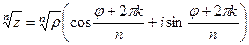
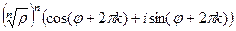 =
= 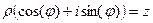 .
.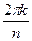 после возведения в степень станет кратной
после возведения в степень станет кратной 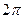 , то есть точка, отстоящая на угол
, то есть точка, отстоящая на угол 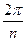 , просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 360 градусов, и придёт в ту же точку, что и было бы без
, просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 360 градусов, и придёт в ту же точку, что и было бы без 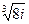 .
.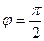 , модуль
, модуль 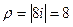 .
.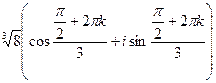 при k = 0,1,2.
при k = 0,1,2. 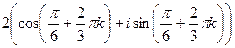 , отсюда:
, отсюда: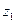 =
= 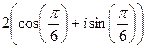 =
= 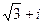
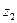 =
= 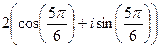 =
= 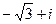
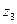 =
= 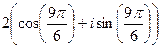 =
= 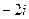
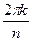 в формуле.
в формуле.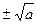 . Это происходит по той же причине: если число было положительным, то его аргумент был 0, и тогда по формуле
. Это происходит по той же причине: если число было положительным, то его аргумент был 0, и тогда по формуле 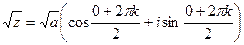 то есть
то есть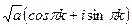 =
= 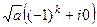 =
= 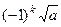 , что и соответствует
, что и соответствует 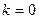 и
и 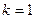 . К аргументу прибавляется по 360 / 2 = 180 градусов.
. К аргументу прибавляется по 360 / 2 = 180 градусов. 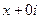 и покажем, что данные функции, а именно
и покажем, что данные функции, а именно 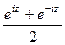 и
и 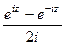 , приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
, приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,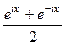 =
= 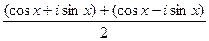 =
= 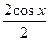 =
= 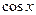
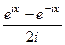 =
= 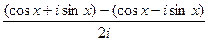 =
= 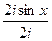 =
= 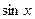
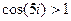 .
.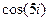 =
= 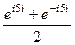 =
= 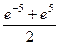
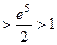 .
.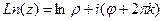 (
(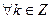 )
)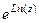 и
и 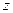 при любом целом
при любом целом 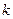 .
.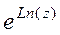 =
= 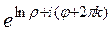 =
= 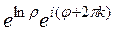 =
= 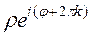 =
=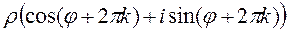 =
=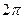 , поэтому получаем
, поэтому получаем 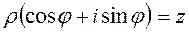 .
.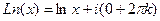 , т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол
, т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол 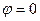 . Для любого числа, которое не является действительным положительным,
. Для любого числа, которое не является действительным положительным, 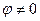 , поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
, поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.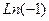 .
.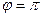 ,
, 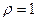 . Поэтому
. Поэтому 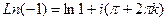 =
= 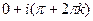 .
.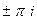 ,
, 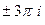 ,
, 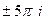 , и так далее.
, и так далее.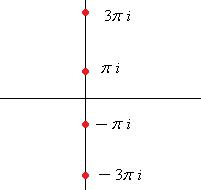
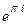 =
= 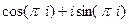 =
= 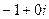 =
= 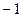 , то есть действительно,
, то есть действительно, 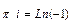 .
.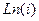 .
.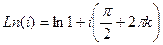 =
= 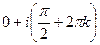 . Последовательность значений такова:
. Последовательность значений такова:  каждая соседняя пара отличается на
каждая соседняя пара отличается на 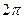 по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для
по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для 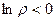 , а если вне единичной окружности, то в правой полуплоскости.
, а если вне единичной окружности, то в правой полуплоскости.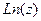 в зависимости от колебаний модуля или аргумента
в зависимости от колебаний модуля или аргумента 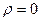 , и не существует
, и не существует 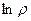 .
.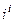 .
.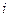 , расположенную в основании, в виде
, расположенную в основании, в виде 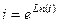 . Тогда
. Тогда 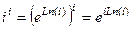 , причём чуть выше мы вычисляли
, причём чуть выше мы вычисляли . Тогда
. Тогда 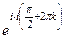 =
= 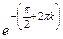 т.е. получается бесконечное множество точек на действительной оси.
т.е. получается бесконечное множество точек на действительной оси.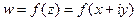 можно отдельно выделить действительную и мнимую части, и представить в виде
можно отдельно выделить действительную и мнимую части, и представить в виде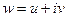 . Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения:
. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения: 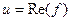 ,
, 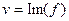 . Итак, комплексной функции можно поставить в соответствие некоторое отображение из
. Итак, комплексной функции можно поставить в соответствие некоторое отображение из 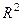 в
в 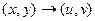 . Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
. Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.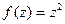 на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе
на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе 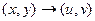 .
.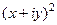 =
= 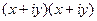 =
= 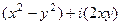 .
.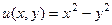 ,
, 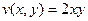 .
.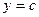 , при этом
, при этом 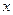 изменяется от
изменяется от 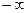 до
до 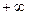 , пусть движение задано с помощью параметра
, пусть движение задано с помощью параметра 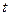 :
: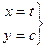
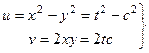 .
.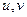 , и узнать, какая это кривая, исключим параметр
, и узнать, какая это кривая, исключим параметр 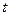 , выразив из второго уравнения:
, выразив из второго уравнения: 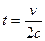 , тогда
, тогда 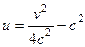 . Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше
. Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше 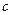 , тем левее вершина, и тем более пологая парабола получается, ведь
, тем левее вершина, и тем более пологая парабола получается, ведь 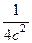 при этом меньше. А если
при этом меньше. А если 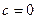 , то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости
, то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости 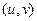 .
.
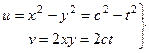 . Тогда, исключая параметр
. Тогда, исключая параметр 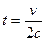
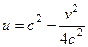 . Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
. Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.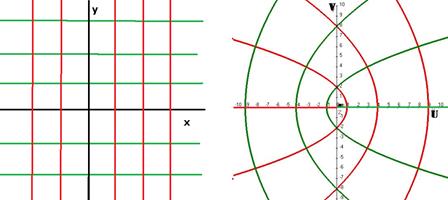
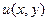 и
и 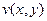 .
.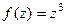 на сумму действительной и мнимой частей.
на сумму действительной и мнимой частей.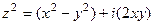 , тогда
, тогда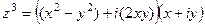 =
= 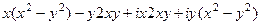 =
= 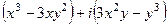 .
.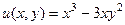
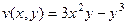 .
.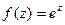 на сумму действительной и мнимой части.
на сумму действительной и мнимой части.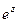 =
= 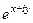 =
= 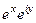 =
= 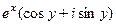 =
= 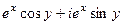 , тогда
, тогда 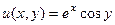 ,
, 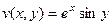 .
. 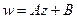 , где коэффициенты
, где коэффициенты 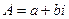 ,
, 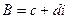 это тоже некоторые комплексные числа. При этом очевидно, что
это тоже некоторые комплексные числа. При этом очевидно, что 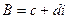 приводит к сдвигу плоскости на вектор
приводит к сдвигу плоскости на вектор 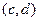 , поэтому сначала более подробно изучим именно
, поэтому сначала более подробно изучим именно 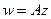 без сдвига.
без сдвига.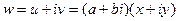 =
= 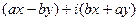 . Но такое отображение можно представить с помощью линейного оператора:
. Но такое отображение можно представить с помощью линейного оператора: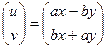 =
= 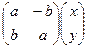 .
.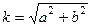 , тогда существует какой-то угол
, тогда существует какой-то угол 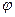 , для которого
, для которого 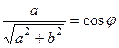 ,
, 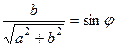 . Причём заметим, что это именно
. Причём заметим, что это именно 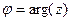 ,
, 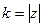 для исходного комплексного числа.
для исходного комплексного числа.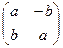 =
= 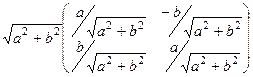 =
= 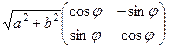 =
= 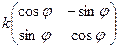 то есть это композиция растяжения и поворота плоскости, причём поворот на угол
то есть это композиция растяжения и поворота плоскости, причём поворот на угол 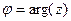 , а растяжение или сжатие на
, а растяжение или сжатие на 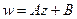 в комплексной плоскости есть композиция растяжения, поворота и сдвига.
в комплексной плоскости есть композиция растяжения, поворота и сдвига.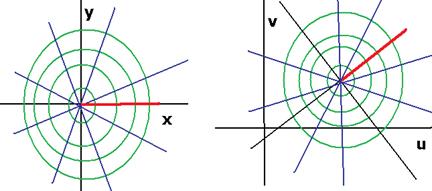
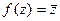 соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.
соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.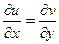 и
и 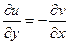 .
.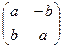 .
. 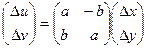 .
.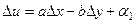
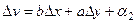 ,
,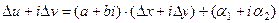 , то есть
, то есть 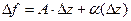 , что и означает дифференцируемость
, что и означает дифференцируемость  .
.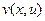 должны быть взаимосвязаны, т.е. если мы произвольно зададим две какие-то функции
должны быть взаимосвязаны, т.е. если мы произвольно зададим две какие-то функции 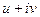 , то не всегда получим какую-то дифференцируемую комплексную функцию.
, то не всегда получим какую-то дифференцируемую комплексную функцию.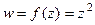 .
.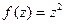 =
= 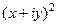 =
= 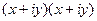 =
=  .
.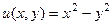 ,
, 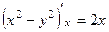 ,
, 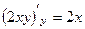 они равны (1-е условие Коши-Римана).
они равны (1-е условие Коши-Римана).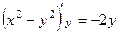 ,
, 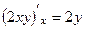 они противоположны (а это и есть
они противоположны (а это и есть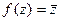 . Тогда
. Тогда 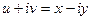 ,
, 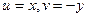 . Не выполняется 1-е условие:
. Не выполняется 1-е условие: 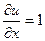 ,
, 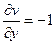 , они не равны ни в одной точке. Геометрически это означает, что зеркальное отражение плоскости невозможно представить в виде композиции растяжения и поворота, то есть невозможно равенство из условия дифференцируемости
, они не равны ни в одной точке. Геометрически это означает, что зеркальное отражение плоскости невозможно представить в виде композиции растяжения и поворота, то есть невозможно равенство из условия дифференцируемости 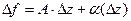 .
.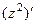 =
= 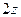 , что в точке
, что в точке 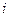 равно
равно 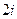 .
.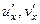 :
: 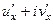 =
= 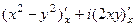 =
= 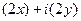 ,
,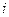 означает что в
означает что в  , т.е. данные функции надо вычислить в точке
, т.е. данные функции надо вычислить в точке 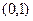 , что составляет
, что составляет 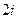 .
. 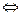 векторные поля
векторные поля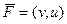 и
и 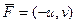 являются потенциальными.
являются потенциальными.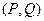 , а именно,
, а именно, 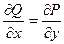 . Для векторного поля
. Для векторного поля 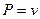 ,
, 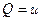 , и тогда условие потенциальности эквивалентно первому условию Коши-Римана
, и тогда условие потенциальности эквивалентно первому условию Коши-Римана  ,
, 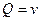 , и тогда условие потенциальности эквивалентно второму условию Коши-Римана:
, и тогда условие потенциальности эквивалентно второму условию Коши-Римана: 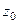 , и во всех точках некоторой её окрестности, то она называется аналитической в точке
, и во всех точках некоторой её окрестности, то она называется аналитической в точке 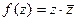 . Распишем её через
. Распишем её через 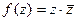 =
= 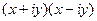 =
= 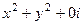 . Здесь
. Здесь 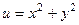 ,
, 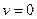 .
.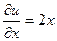 ,
, 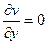 .
.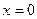
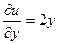 ,
, 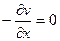 .
.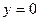 .
.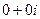 . То есть, в начале координат функция дифференцируемая, но не аналитическая.
. То есть, в начале координат функция дифференцируемая, но не аналитическая.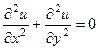 и
и 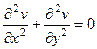 .
.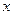 , а второе по
, а второе по 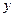 :
: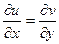

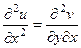
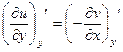
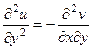 .
.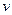 при этом совпадают, они вычитаются и дают 0.
при этом совпадают, они вычитаются и дают 0.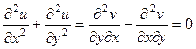 . Итак,
. Итак, 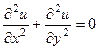 .
.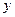 , а второе по
, а второе по 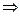
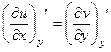
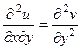
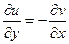
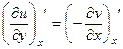
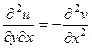 .
.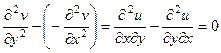 , тогда
, тогда 


