
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Муавра, степень. Корни.
Возводить комплексные числа в степень можно с помощью такой формулы: она называется формулой Муавра и позволяет не перемножать множество скобок, если требуется вычислить большую степень числа Доказательство. Если умножим в тригонометрической форме не два разных числа, а одно и то же число
Таким же образом можно умножить
Таким образом, по индукции, можно доказать, что
Но ещё легче возводить в степень с помощью показательной формы числа: Пример. Найти Вычислим модуль и аргумент.
По формуле Муавра, В показательной форме: ЛЕКЦИЯ № 2. 9.09.2020 Корни порядка n. Корень порядка n вычисляется по такой формуле:
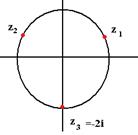
Доказательство. Если возведём в степень n, получим Добавка Пример. Найдите все значения корня Сначала представим комплексное число, которое находится под знаком корня, в тригонометрической форме. Точка расположена на мнимой оси выше начала координат, поэтому аргумент Теперь находим все 3 корня.
1) 2) 3) Чертёж:
Если к исходному углу добавить 120 градусов, то для куба этого числа добавится 360 градусов, и результат будет точно такой же. С этим фактом как раз и связано наличие лишнего слагаемого
Квадратных корней два, а именно
Области в комплексной плоскости и неравенства, задающие их.
Пример. Пример. Множество Пример. Функции комплексного переменного. Обобщим на комплексную плоскость синус и косинус. Верны такие формулы: Доказательство. Рассмотрим для действительного числа 1) 2)
Неограниченность синуса и косинуса в комплексной плоскости. Пример. Вычислим:
Логарифм комплексного числа.
Обобщённый логарифм вводится с помощью формулы:
Доказательство. Проверим, совпадает ли
синус и косинус не зависят от прибавления угла, кратного А это уже и есть тригонометрическая форма комплексного числа. Итак, Если вычислять логарифм положительного действительного числа, то Пример. Вычислить Здесь Точки в комплексной плоскости: Ни одного значения на действительной оси нет, и здесь, по сравнению со значениями логарифма положительного числа, сдвиг на половину деления: одна точка ушла вверх с действительной оси, а другая ещё не достигла этой оси. Чертёж:
Здесь легко сделать и проверку: Пример. Вычислить
1) При фиксированном модуле исходного числа и увеличении его аргумента, эта последовательность точек плывёт вверх, при полном повороте на
2) При фиксированном аргументе исходного числа и увеличении его модуля, эта последовательность точек плывёт вправо, если исходная точка внутри единичной окружности то множество значений логарифма в левой полуплоскости, так как Динамическая анимация, показывающая поведение значений http://www.youtube.com/watch?v=LKFFn-TSLd0
Замечание. Единственная точка в комплексной плоскости, для которой не существует логарифма, это 0. Ведь в этом случае
Пример. Вычислить Решение. Представим
Для всякой функции
Пример. Разложить 1) Таким образом, Чтобы исследовать, куда переходят горизонтальные прямые, зафиксируем
Чтобы составить уравнение, взаимосвязывающее Аналогично, для какой-либо вертикальной прямой:
На чертеже зелёным цветом показаны горизонтальные прямые и их образы при отображении
Примечание. 4-мерный график можно было бы рассматривать таким образом: нужно как минимум 4 проекции на координатные пространства, а именно 0xyz, 0xzw, 0xyw, 0yzw. Либо можно рассмотреть 2 поверхности, построенные по функциям Пример. Разложить Используем то, что нашли ранее:
Здесь Пример. Разложить По формуле Эйлера:
ЛЕКЦИЯ № 3. 16.09.2020 Изучим подробнее линейное отображение, какие деформации плоскости происходят при действии линейной функции вида
Введём величину Тогда матрица линейного оператора имеет вид (домножим и поделим на квадратный корень):
Доказали, что линейное отображение
На этом чертеже показано, как изменяется плоскость при линейном отображении. Красным веделено горизонтальное направление, после отображения оно повёрнуто.
Замечание. Отображение
|
|||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.139.162 (0.051 с.) |
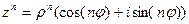
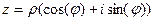 , то получим:
, то получим: 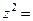
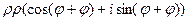 =
=  .
.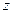 в третий раз и снова в аргументе прибавится
в третий раз и снова в аргументе прибавится  , а модуль снова умножится на
, а модуль снова умножится на 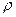 .
.
 =
=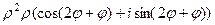 =
= 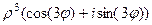
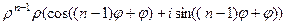 =
= 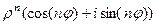 .
. 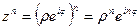 , здесь даже доказывать по индукции нет необходимости.
, здесь даже доказывать по индукции нет необходимости. по формуле Муавра.
по формуле Муавра.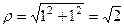
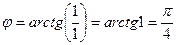 .
.
 =
=  =
=  = 16.
= 16. =
= 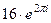 =
= 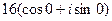 = 16.
= 16.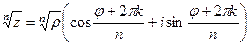
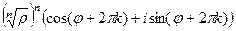 =
= 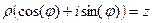 .
.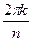 после возведения в степень станет кратной
после возведения в степень станет кратной 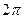 , то есть точка, отстоящая на угол
, то есть точка, отстоящая на угол 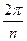 , просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 360 градусов, и придёт в ту же точку, что и было бы без
, просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 360 градусов, и придёт в ту же точку, что и было бы без 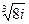 .
.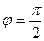 , модуль
, модуль 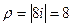 .
.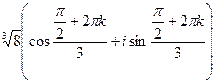 при k = 0,1,2.
при k = 0,1,2. 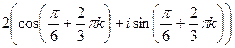 , отсюда:
, отсюда: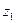 =
= 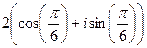 =
= 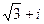
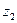 =
= 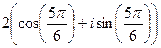 =
= 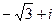
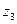 =
= 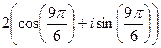 =
= 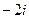
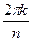 в формуле.
в формуле.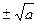 . Это происходит по той же причине: если число было положительным, то его аргумент был 0, и тогда по формуле
. Это происходит по той же причине: если число было положительным, то его аргумент был 0, и тогда по формуле 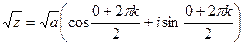 то есть
то есть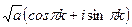 =
= 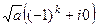 =
= 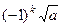 , что и соответствует
, что и соответствует 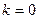 и
и 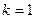 . К аргументу прибавляется по 360 / 2 = 180 градусов.
. К аргументу прибавляется по 360 / 2 = 180 градусов. 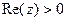 правая полуплоскость.
правая полуплоскость. верхняя полуплоскость.
верхняя полуплоскость.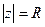 - окружность радиуса R вокруг начала координат.
- окружность радиуса R вокруг начала координат. 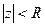 - круг радиуса R вокруг начала координат.
- круг радиуса R вокруг начала координат. 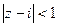 это круг радиуса 1 вокруг точки
это круг радиуса 1 вокруг точки 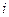 . Это неравенство задаёт следующее условие: удаление числа
. Это неравенство задаёт следующее условие: удаление числа 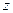 от фиксированного числа
от фиксированного числа 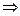
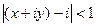
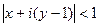

 а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке
а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке 

 это круг радиуса 2 с центром в точке
это круг радиуса 2 с центром в точке 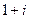 , то есть точке (1,1) в плоскости.
, то есть точке (1,1) в плоскости.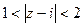 это кольцо вокруг точки
это кольцо вокруг точки  это круг радиуса
это круг радиуса  вокруг точки
вокруг точки  .
.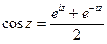 ,
, 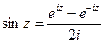 .
.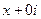 и покажем, что данные функции, а именно
и покажем, что данные функции, а именно 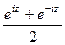 и
и 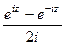 , приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
, приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,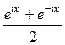 =
= 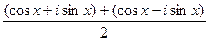 =
= 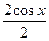 =
= 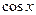
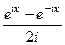 =
= 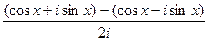 =
= 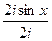 =
= 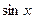
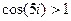 .
.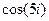 =
= 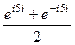 =
= 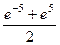
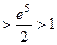 .
.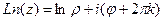 (
(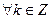 )
)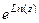 и
и 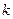 .
.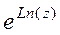 =
= 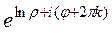 =
= 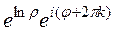 =
= 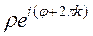 =
=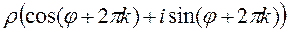 =
=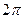 , поэтому получаем
, поэтому получаем 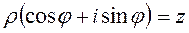 .
.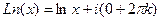 , т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол
, т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол 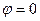 . Для любого числа, которое не является действительным положительным,
. Для любого числа, которое не является действительным положительным, 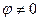 , поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
, поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.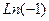 .
.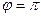 ,
, 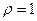 . Поэтому
. Поэтому 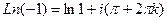 =
= 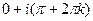 .
.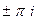 ,
, 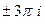 ,
, 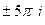 , и так далее.
, и так далее.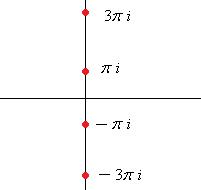
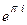 =
= 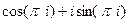 =
= 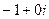 =
= 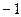 , то есть действительно,
, то есть действительно, 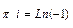 .
.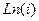 .
.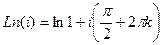 =
= 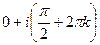 . Последовательность значений такова:
. Последовательность значений такова:  каждая соседняя пара отличается на
каждая соседняя пара отличается на 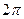 по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для
по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для 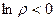 , а если вне единичной окружности, то в правой полуплоскости.
, а если вне единичной окружности, то в правой полуплоскости. в зависимости от колебаний модуля или аргумента
в зависимости от колебаний модуля или аргумента 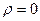 , и не существует
, и не существует 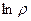 .
.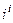 .
.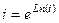 . Тогда
. Тогда 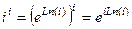 , причём чуть выше мы вычисляли
, причём чуть выше мы вычисляли . Тогда
. Тогда 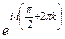 =
= 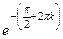 т.е. получается бесконечное множество точек на действительной оси.
т.е. получается бесконечное множество точек на действительной оси.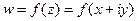 можно отдельно выделить действительную и мнимую части, и представить в виде
можно отдельно выделить действительную и мнимую части, и представить в виде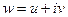 . Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения:
. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения: 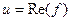 ,
, 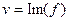 . Итак, комплексной функции можно поставить в соответствие некоторое отображение из
. Итак, комплексной функции можно поставить в соответствие некоторое отображение из 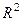 в
в 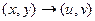 . Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
. Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.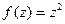 на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе
на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе 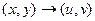 .
.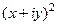 =
= 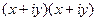 =
= 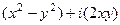 .
.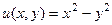 ,
, 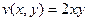 .
.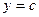 , при этом
, при этом 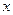 изменяется от
изменяется от 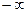 до
до 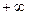 , пусть движение задано с помощью параметра
, пусть движение задано с помощью параметра 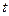 :
: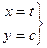
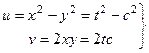 .
.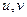 , и узнать, какая это кривая, исключим параметр
, и узнать, какая это кривая, исключим параметр 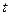 , выразив из второго уравнения:
, выразив из второго уравнения: 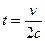 , тогда
, тогда 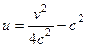 . Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше
. Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше 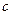 , тем левее вершина, и тем более пологая парабола получается, ведь
, тем левее вершина, и тем более пологая парабола получается, ведь 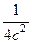 при этом меньше. А если
при этом меньше. А если 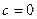 , то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости
, то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости 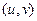 .
.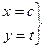
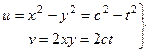 . Тогда, исключая параметр
. Тогда, исключая параметр 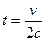
 . Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
. Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.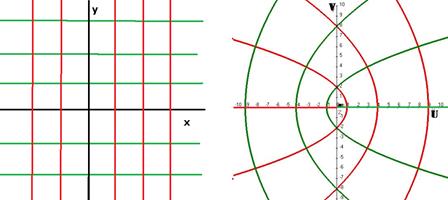
 и
и  .
.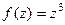 на сумму действительной и мнимой частей.
на сумму действительной и мнимой частей.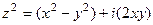 , тогда
, тогда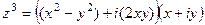 =
= 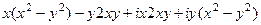 =
= 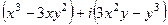 .
.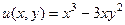
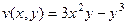 .
.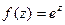 на сумму действительной и мнимой части.
на сумму действительной и мнимой части.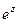 =
= 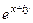 =
= 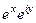 =
= 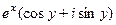 =
= 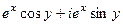 , тогда
, тогда 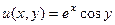 ,
, 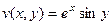 .
. 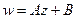 , где коэффициенты
, где коэффициенты 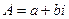 ,
, 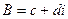 это тоже некоторые комплексные числа. При этом очевидно, что
это тоже некоторые комплексные числа. При этом очевидно, что 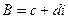 приводит к сдвигу плоскости на вектор
приводит к сдвигу плоскости на вектор 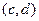 , поэтому сначала более подробно изучим именно
, поэтому сначала более подробно изучим именно 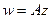 без сдвига.
без сдвига.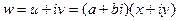 =
= 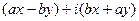 . Но такое отображение можно представить с помощью линейного оператора:
. Но такое отображение можно представить с помощью линейного оператора: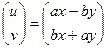 =
= 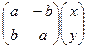 .
.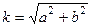 , тогда существует какой-то угол
, тогда существует какой-то угол 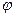 , для которого
, для которого 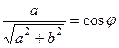 ,
, 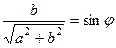 . Причём заметим, что это именно
. Причём заметим, что это именно 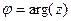 ,
, 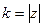 для исходного комплексного числа.
для исходного комплексного числа.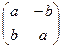 =
= 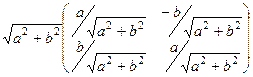 =
= 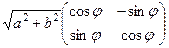 =
= 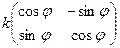 то есть это композиция растяжения и поворота плоскости, причём поворот на угол
то есть это композиция растяжения и поворота плоскости, причём поворот на угол 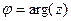 , а растяжение или сжатие на
, а растяжение или сжатие на 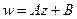 в комплексной плоскости есть композиция растяжения, поворота и сдвига.
в комплексной плоскости есть композиция растяжения, поворота и сдвига.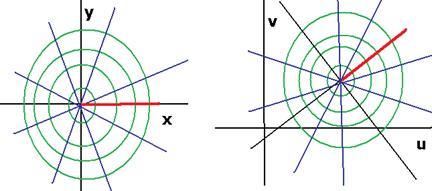
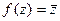 соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.
соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.


