
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
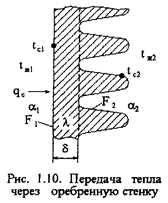
Передача тепла через оребренные поверхности
Одним из методов интенсификации теплопередачи является оребрение поверхности. Пусть имеется плоская стенка толщиной δ, на одной стороне которой имеются ребра (см. рис. 1.10.)
Температура гладкой поверхности и простенков между ними равна tc2. Коэффициент теплопроводности стенки и ребер λ. Коэффициент теплоотдачи на гладкой стороне α1, на ребристой α2. Площадь гладкой поверхности F1, площадь поверхности ребер и промежутков между ними F2. Температура горячего теплоносителя t1, холодного t2. Тогда тепловой поток через ребристую поверхность
где kp — коэффициент теплопередачи для оребренной поверхности, Вт/(м2× K) равен
Если тепловой поток отнести к единице гладкой поверхности стенки, то
где kр.г — имеет размерность Вт/(м2× K). Если тепловой поток отнести к единице ребристой поверхности стенки, то получим:
Для круглой трубы с наружным оребрением формула (1.55) приобретает вид:
где kр.к — имеет размерность Вт/(м×K).
Отношение оребренной поверхности F2 к гладкой F1 называется коэффициентом оребрения.
Теплопроводность при нестационарном режиме Передачу тепла при нестационарном режиме можно определить, если найти закон изменения температурного поля и теплового потока во времени и в пространстве
где x, y, z — координаты точки; t — время Указанные зависимости могут быть найдены из решения дифференциального уравнения теплопроводности
При решении уравнения (1.64) необходимо задать граничные условия и начальное распределение температуры в теле Граничные условия задаются уравнением
где α — коэффициент теплоотдачи между жидкой средой и твердой поверхностью; λ — теплопроводность стенки; tпов — температура поверхности стенки; tсреды — температура окружающей среды. Физические величины λ, r, с считаются постоянными. Решение уравнений (1.61) и (1.62) с учетом граничных и начальных условий дает уравнение температурного поля вида:
Анализ уравнения (1.67) показывает, что переменные можно сгруппировать в три безразмерных комплекса:
Bi — число Био; Fo — число Фурье; Θ — безразмерная температура. Неограниченная пластина Рассмотрим охлаждение плоскопараллельной пластины толщиной 2 δ. Размеры пластины в направлении осей Оy и Оz бесконечно велики. Пластина омывается с двух сторон жидкостью или газом с постоянной температурой t, причем коэффициент теплоотдачи α для обеих поверхностей имеет одинаковое и постоянное значение. В начальный момент времени пластина имеет во всех своих точках постоянную температуру t, поэтому и избыточная безразмерная температура Θ будет также постоянной для всех точек тела. Температуры поверхности стенки и в ее средней плоскости определяют из соотношения:
Безразмерная координата x/l в средней плоскости и на поверхности пластины становится постоянной (при x=0 x/l=0; при x= δ x/l=1) и поэтому ее нет в предыдущем уравнении:
Количество теплоты, которое отдает (или воспринимает) пластина в окружающую среду за время τ, должно равняться изменению ее внутренней энергии за период полного ее охлаждения (нагревания).
где Тогда внутренняя энергия пластины за промежуток времени от τ = 0 до τ изменится на величину
где
При Bi
Если Bi
При значениях числа Fo
Множитель
Цилиндр бесконечной длины Рассмотрим охлаждение равномерно прогретого круглого цилиндра радиусом r в среде с меньшей температурой. Физические параметры цилиндра не зависят от температуры и не меняются во времени. Коэфициент теплоотдачи среды α. Необходимо определить температуру поверхности, температуру центра и количество тепла, отданное в окружающую среду, для любого момента времени.
Температуры на поверхности, на центральной оси и теплопотери цилиндра через произвольные промежутки времени определяются из следующих соотношений:
Для цилиндрической стенки
где r — радиус цилиндрической стенки.
Величины а затем по ним находят Внутренюю энергию рассматриваемого участка цилиндра длиной l, отсчитанную от ее значения при температуре среды, как от нуля, находим по формуле
Аналогично, как для пластины, количество теплоты, которое отдается или воспринимается цилиндром за промежутое времени от τ = 0 до τ1, находится по формуле:
где — корни характеристического уравнения. При расчете средней температуры цилиндра в случае Fo
Функция
заранее рассчитана для соответствующих значений Bi и сведена в таблицу. Шар Рассмотрим охлаждение шара радиусом r, равномерно прогретого до постоянной температуры в среде с более низкой температурой. Физические постоянные для которого и коэффициент теплоотдачи известны. Определить для любого момента времени температуру поверхности, температуру в центре шара и количество теплоты, теряемое шаром в окружающую среду. Задача на охлаждение шара аналогична предыдущим задачам. Для шара
где r — радиус шара. Зависимости между безразмерными величинами определяются по номограммам, а затем по ним определяются Начальная внутренняя энергия шара отсчитывается от ее значения при температуре среды, как от нуля, по формуле
Аналогично, как для пластины и цилиндра, количество теплоты, которое отдается или воспринимается шаром за промежуток времени от τ = 0 до τ1, находится по формуле:
Примеры решения задач 1.Плоская стенка выполнена из шамотного кирпича толщиной δ =250 мм. Температура ее поверхности: tс1 =1350 °С и tс2=50 °С. Коэффициент теплопроводности шамотного кирпича является функцией от температуры λ=0,838(1+0,0007·t). Вычислить распределение температуры в стенке для следующих значений x мм: 0; 50; 100; 125; 150; 200; 225; 250. Решение 1. В случае линейной зависимости коэффициента теплопроводности от температуры плотность теплового потока, Вт/м2 определяется по выражению:
где средний коэффициент теплопроводности, Вт/(м × К)
2. Определяем λ ср
3. Определяем плотность теплового потока
Температура на любом расстоянии x от поверхности стенки определяется по формуле
4. Определяем t
5. Определяем соответствующие значения температур путем подстановки в последнее выражение значений x.
2.Рассчитать нагрев пластины в прямотоке для следующих исходных данных: W=0,2; tнач=20 σд = 3,0 Вт/(м2 Находим относительные температуры нагреваемого материала:
Вычисляем число Старка:
Определяем начальное значение функции:
Выбираем шаг по температуре нагреваемого материала
и вычисляем соответствующие значения функций
Находим для этого значения температуры нагреваемого материала безразмерное время:
относительную температуру греющих газов:
безразмерную плотность теплового потока:
Аналогично расчеты для всех остальных значений результаты которых занесены в табл.1. и показаны в виде температурной и тепловой диаграмм.
Таблица 1. Результаты расчета нагрева пластины в прямотоке при W =0,2 и Sk =0,1
3.По трубе диаметром d1/d2 = 18/20мм течет насыщенный водяной пар. Для уменьшения тепловых потерь в окружающую среду трубу необходимо изолировать. Целесообразно ли использовать для этого асбест с λ = 0,11Вт/мК, если коэффициент теплоотдачи с внешней поверхности изоляции к окружающей среде α = 811Вт/м2К? Решение Определяем критический диаметр изоляции
т.к. dкр>d2, использовать асбест нельзя.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-14; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.41.214 (0.038 с.) |
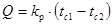
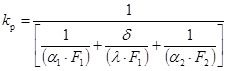
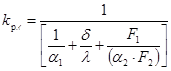
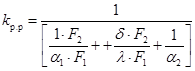
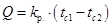
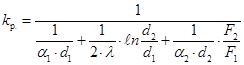
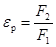 .
.
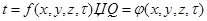
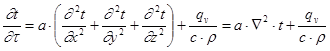
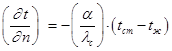
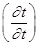 — градиент температуры на поверхности;
— градиент температуры на поверхности;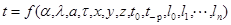
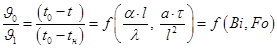
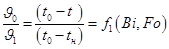
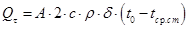
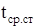 — средняя температура стенки по истечении периода времени τ, с.
— средняя температура стенки по истечении периода времени τ, с.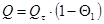
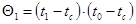 — средняя безразмерная температура по толщине пластины в момент времени τ.
— средняя безразмерная температура по толщине пластины в момент времени τ.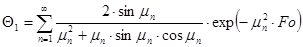
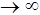 уравнение (1.72) принимает вид:
уравнение (1.72) принимает вид: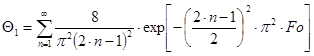
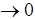 уравнение (1.72) принимает вид
уравнение (1.72) принимает вид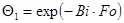
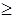 0,3
0,3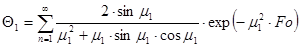

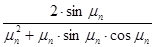 зависит только от числа Bi и может быть представлен в виде функции P=f(Bi), которая табулирована и имеется в Приложении (1). Тогда уравнение (1.75) будет иметь вид:
зависит только от числа Bi и может быть представлен в виде функции P=f(Bi), которая табулирована и имеется в Приложении (1). Тогда уравнение (1.75) будет иметь вид: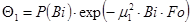
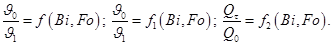
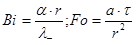
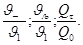 определяют по графикам,
определяют по графикам,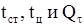 .
.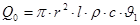
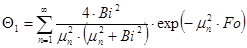
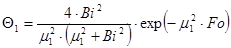
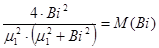
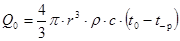
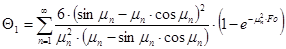
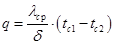
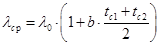
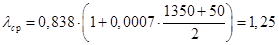
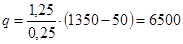
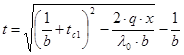
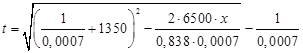
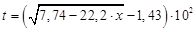
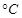 ;
; 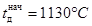 ; S=0,05 м; λ = 48 Вт/(м
; S=0,05 м; λ = 48 Вт/(м  K);
K);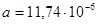 м2/с.
м2/с.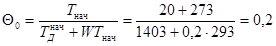 ;
;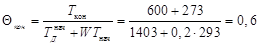 .
.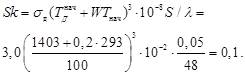
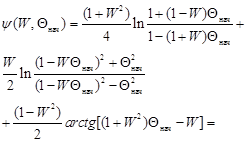
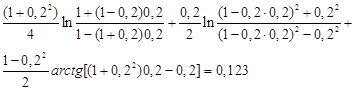 .
.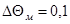
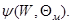 Так, для
Так, для 
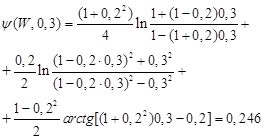
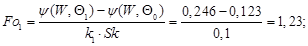
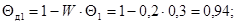
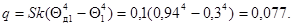
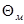 ,
,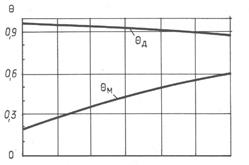 Анализ решения показывает, что при W<1 имеет место снижение плотности теплового потока по ходу нагрева металла, в связи с чем температуры теплообменивающихся сред сближаются. Однако если при линейных граничных условиях падение теплового потока происходит по вогнутой кривой, то при лучистом теплообмене — по выпуклой кривой.
Анализ решения показывает, что при W<1 имеет место снижение плотности теплового потока по ходу нагрева металла, в связи с чем температуры теплообменивающихся сред сближаются. Однако если при линейных граничных условиях падение теплового потока происходит по вогнутой кривой, то при лучистом теплообмене — по выпуклой кривой.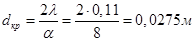 ;
;


