
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители квадратной матрицы. Утверждения 1-3. Общие свойства определителя квадратной матрицы
Определитель обозначается Первый способ нахождения определителя (подходит только для матриц размерности Второй способ нахождения определителя. Через алгебраические дополнения.
Третий способ нахождения определения. С помощью неособенных элементарных преобразований обнуляем все элементы ниже главной диагонали, а затем находим её произведение. Это и есть наш определитель. Следует учесть (1): 1. перестановка двух строк местами поменяет знак определителя на противоположный 2. умножение элементов строки на элемент k≠0 увеличивает искомый определитель в k раз 3. прибавление к какой-либо строке элементов другой строки, предварительно умноженных на некоторое число, не меняет значение определителя Утверждение 1. Если квадратная матрица содержит нулевую строку, то её определитель равняется нулю. Утверждение 2.??? Утверждение 3. Определитель треугольной матрицы (т.е. матрицы, в которой все элементы выше и ниже нулевой строки равны 0) равен произведению элементов главной диагонали. Общие свойства квадратных матриц (7 свойств): · · (1) · Определитель квадратной матрицы, содержащей две одинаковые строки, равен 0. · Определитель квадратной матрицы не меняется, если к элементам какой-либо строки/столбца прибавить линейную комбинацию других строк/столбцов квадратной матрицы. · Если определители одной из строк/столбцов является линейной комбинацией других строк/столбцов, определитель равен 0. Миноры и алгебр. дополнения Подматрица матрицы A – матрица, полученная из матрицы A, путём удаления из неё строки i и столбца j. Подматрица k-ого порядка – подматрица размерности Минор k-ого порядка – определитель подматрицы k-ого порядка. Алгебраическое дополнение
Теорема 1. Если в квадратной матрице A элементы в последней строке быть может за исключением элементы Теорема 2. Если в квадратной матрице A элементы в какой-либо строке за исключением одного элементы равны нулю, то определитель высчитывается по формуле: При разложении определителя квадратной матрицы по элементам выбранной строки(столбца) следует учитывать эти две теоремы:
Теорема 1. Пусть дана Замечание. Теорема остаётся верной и при разложении по j (т.е. по строкам). Теорема 2. Сумма произведений элементов одной из строк на алгебраические дополнения другой строки равна 0.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 39; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.173.112 (0.004 с.) |
 .
.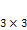 ). По правилу треугольника.
). По правилу треугольника. 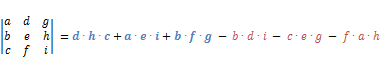
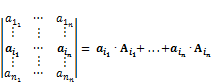 (j можно выбрать произвольный)
(j можно выбрать произвольный)
 .
.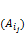 – соответствующий минор, взятый со знаком, определяемым по формуле (-1)i+j.
– соответствующий минор, взятый со знаком, определяемым по формуле (-1)i+j.
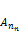 равны нулю, то определитель высчитывается по формуле:
равны нулю, то определитель высчитывается по формуле: 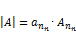 .
.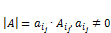 .
.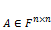 , тогда
, тогда 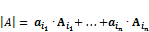 .
.


