
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы. Нулевая матрица. Единичная матрица. Операции над матрицамиСтр 1 из 7Следующая ⇒
Матрицы. Нулевая матрица. Единичная матрица. Операции над матрицами Поле – некоторое множество с введёнными над этим множеством операциями сложения, вычитания, умножения, деления и выделенным нейтральным элементом, относительно операции умножения.
Для её обозначения используют символ: · Если · Если Все элементы · Матрица называется нулевой, если все её элементы равны 0 (обозначается через латинскую букву · Матрица называется единичной, если элементы её главной диагонали равны 1, а вне этой диагонали равны 0 (обозначается через латинскую букву
Матрицы равны, если совпадают их размерности и соответствующие элементы. Чтобы сложить матрицы одинаковых размерностей следует сложить их соответствующие элементы, аналогично с вычитанием. Умножение на скаляр: Матрица Умножение матриц: при умножении матриц
Свойства операций над матрицами. Для любых двух матриц 1. 2. 3. 4. 5. 6. 7. 8. Транспонированные матрицы. Теорема о транспонировании произведения квадратных матриц Транспонированная матрица получается заменой в матрице строк соответствующими столбцами (обозначается через Теорема. Если Миноры и алгебр. дополнения Подматрица матрицы A – матрица, полученная из матрицы A, путём удаления из неё строки i и столбца j. Подматрица k-ого порядка – подматрица размерности Минор k-ого порядка – определитель подматрицы k-ого порядка.
Алгебраическое дополнение
Теорема 1. Если в квадратной матрице A элементы в последней строке быть может за исключением элементы Теорема 2. Если в квадратной матрице A элементы в какой-либо строке за исключением одного элементы равны нулю, то определитель высчитывается по формуле: При разложении определителя квадратной матрицы по элементам выбранной строки(столбца) следует учитывать эти две теоремы: Теорема 1. Пусть дана Замечание. Теорема остаётся верной и при разложении по j (т.е. по строкам). Теорема 2. Сумма произведений элементов одной из строк на алгебраические дополнения другой строки равна 0. Полярная система координат · Рассмотрим · Соединим · Пусть · Пусть угол между · · · · Уравнение прямой в отрезках Если
Другими словами, прямая отсекает от Общее уравнение плоскости · Разложим по первой строке доказанную в прошлой теме теорему:
· Введём обозначения:
· Обозначим через · Имеем общее уравнение плоскости:
Здесь Верно и обратное утверждение. Всякое решение (2) определяет точку с координатами Замечание: вектор · Возьмём две лежащие на плоскости точки: · Координаты этих точек должны удовлетворять (2):
· Вычтем из (4) (3):
· Это равенство, по сути, представляет собой скалярное произведение, равное нулю:
· · Так как 38. Критерий компланарности вектора и плоскости. Теорема Теорема. Пусть относительно прямоугольно-декартовой системы координат заданы вектор
Доказательство: · Отложим вектор · Конец Р отложенного вектора будет иметь координаты · Вектор коллинеарен заданной плоскости тогда и только тогда, когда точка Р лежит в данной плоскости, т.е. выполняется уравнение (2):
· · После раскрытия скобок с учётом уравнения выше остаётся условие:
Из этой теоремы следует, что главный вектор плоскости 39. Уравнение плоскости, проходящей через 2 заданные точки и компланарной ненулевому вектору. Теоремы 1-3 Теорема. Пусть относительно прямоугольно-декартовой системы координат заданы две точки
Доказательство: · Пусть три точки · Векторы с координатами · Следовательно, матрица из их координат равняется 0. Обратная теорема. Всякое решение уравнения (1) определяет точку с координатами Теорема: Пусть относительно прямоугольно-декартовой системы координат заданы
Доказательство: · Пусть · Возьмём произвольным образом точку · Следовательно, определитель, составленный из их координат, равен 0 ч.т.д. Обратная теорема. Всякое решение уравнения (2) определяет точку, лежащую на плоскости.
Цилиндры второго порядка Матрицы. Нулевая матрица. Единичная матрица. Операции над матрицами Поле – некоторое множество с введёнными над этим множеством операциями сложения, вычитания, умножения, деления и выделенным нейтральным элементом, относительно операции умножения.
Для её обозначения используют символ: · Если · Если Все элементы · Матрица называется нулевой, если все её элементы равны 0 (обозначается через латинскую букву · Матрица называется единичной, если элементы её главной диагонали равны 1, а вне этой диагонали равны 0 (обозначается через латинскую букву
Матрицы равны, если совпадают их размерности и соответствующие элементы. Чтобы сложить матрицы одинаковых размерностей следует сложить их соответствующие элементы, аналогично с вычитанием. Умножение на скаляр: Матрица Умножение матриц: при умножении матриц
|
|||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 38; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.8.247 (0.05 с.) |
 – матрица или матрица над полем L – это таблица вида
– матрица или матрица над полем L – это таблица вида 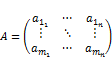 , при чём
, при чём  , а
, а  , где F – множество скаляров, по которым введены основные арифметические операции в поле
, где F – множество скаляров, по которым введены основные арифметические операции в поле 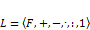 с нейтральным элементом 1.
с нейтральным элементом 1. , где
, где  ,
, 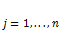 , где i – номер строки, а j – номер столбца, а множество всех
, где i – номер строки, а j – номер столбца, а множество всех  - матриц обозначают через
- матриц обозначают через 
 , то матрица – прямоугольная.
, то матрица – прямоугольная. , то матрица – квадратная.
, то матрица – квадратная. матрицы
матрицы  при i = j называются элементами главной диагонали
при i = j называются элементами главной диагонали ).
). ).
).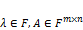 , тогда
, тогда  , где
, где  противоположна матрице
противоположна матрице  . При этом выполняется условие
. При этом выполняется условие  .
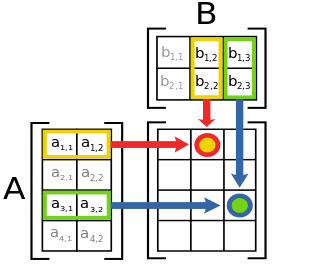
. важно учитывать, что количество столбцов в A должно совпадать c количеством строк в B. Если
важно учитывать, что количество столбцов в A должно совпадать c количеством строк в B. Если  , то результатом будем матрица размерностью
, то результатом будем матрица размерностью  . Для большего понимания можно элементы из этого изображения, где элемент первой строки второго столбца, например, считается как
. Для большего понимания можно элементы из этого изображения, где элемент первой строки второго столбца, например, считается как  :
:
 справедливо:
справедливо: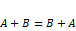

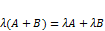 , где
, где  – скаляр
– скаляр , где
, где 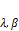 – скаляры
– скаляры , где
, где  , где C – матрица и
, где C – матрица и  ,
, 
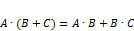 , если
, если 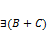
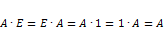
 ).
).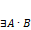 и
и 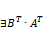 , то
, то 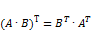
 .
.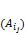 – соответствующий минор, взятый со знаком, определяемым по формуле (-1)i+j.
– соответствующий минор, взятый со знаком, определяемым по формуле (-1)i+j.
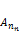 равны нулю, то определитель высчитывается по формуле:
равны нулю, то определитель высчитывается по формуле: 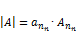 .
.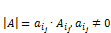 .
.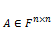 , тогда
, тогда 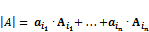 .
.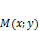 , заданную в прямоугольно-декартовой системе координат на плоскости.
, заданную в прямоугольно-декартовой системе координат на плоскости.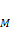 c началом координат (
c началом координат (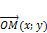 .
.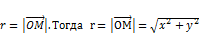 .
. и осью
и осью  равен
равен  .
.


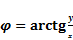
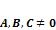 , то уравнение (1) можно записать в виде уравнения прямой в отрезках на плоскости:
, то уравнение (1) можно записать в виде уравнения прямой в отрезках на плоскости: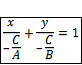
 отрезок
отрезок 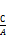 , а на
, а на 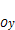 отрезок
отрезок  и проходит через точки
и проходит через точки  ,
, 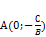 .
.


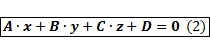
 , так как векторы
, так как векторы  ;
; 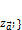 и
и 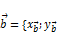 ;
; 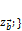 не коллинеарны, а значит определители в разложении одновременно не равны нулю для
не коллинеарны, а значит определители в разложении одновременно не равны нулю для 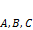 .
.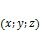 , лежащую на плоскости.
, лежащую на плоскости.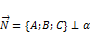 , где
, где  – плоскость, заданная (2). Доказательство:
– плоскость, заданная (2). Доказательство: и
и 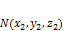 .
.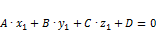 (3)
(3) (4)
(4)

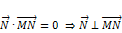
 , то
, то 
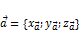 и плоскость, заданная (2). Тогда необходимое и достаточное условие компланарности вектора
и плоскость, заданная (2). Тогда необходимое и достаточное условие компланарности вектора  и данной плоскости имеет вид:
и данной плоскости имеет вид: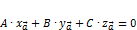
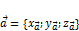 от произвольной точки
от произвольной точки 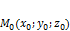 заданной плоскости.
заданной плоскости. .
. .
.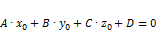 .
. .
.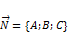 , заданной общим уравнением плоскости относительно общей декартовой системы координат, не компланарен этой плоскости:
, заданной общим уравнением плоскости относительно общей декартовой системы координат, не компланарен этой плоскости:  .
. и
и  и ненулевой вектор
и ненулевой вектор 
 ,
,  точка с координатами
точка с координатами 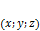 , а также
, а также  .
.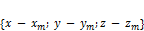 ,
,  ,
,  ,
,  . Тогда уравнение плоскости, проходящей через три точки, не лежащие на одной прямой:
. Тогда уравнение плоскости, проходящей через три точки, не лежащие на одной прямой:
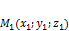 ,
,  ,
, 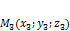 лежат на одной плоскости.
лежат на одной плоскости. , лежащую на плоскости, тогда векторы
, лежащую на плоскости, тогда векторы  ,
, 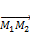 ,
, 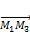 коллинеарны, так как лежат в одной плоскости.
коллинеарны, так как лежат в одной плоскости.


