Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенства. Предельные числа.
Определение 8.1. A+ < B+ Таким образом, для того, чтобы порядковое число множества A+ было меньше порядкового числа множества B+, необходимо и достаточно, чтобы множество A+ было подобно некоторому начальному отрезку множества B+. Заметим, что из определения 8.1 и леммы 7.8 следует:
Из определения 8.1 и теоремы 2.1а следует: Следствие 8.1. Для упрощения записи дальнейших доказательств мы введем следующие обозначения: α = β = γ = Таким образом, буквы α, β, γ в дальнейшем будут обозначать порядковые числа. Из определения 8.1 и леммы 7.3 следует: Лемма 8.1. α < β Лемма 8.2. α Лемма 8.3. α < β Доказательство. Из определения 8.1 и условий леммы следует, что для некоторого элемента b множества B+ и некоторого элемента c множества C+ имеют место соотношения: (1) A+ (2) B+ Из леммы 7.1 и (2) следует существование такого элемента множества C+, что B(b) A+ Таким образом, по определению 8.1 α < γ. Лемма 8.4. α < β Доказательство. Пусть – вопреки тому, что требуется доказать, – β < α. Отсюда и из леммы 8.3 следует, что α < α. Однако данное заключение противоречит лемме 8.1. Из лемм 8.2, 8.3, 8.4 следует Теорема 8.1. Отношение «меньше» упорядочивает множество порядковых чисел. Теорема 8.2. Если множество
Доказательство. Пусть α = A+. Для доказательства теоремы достаточно показать, что
Отношение, устанавливающее подобие данных множеств, есть отношение
Из теоремы 8.2 и следствия 6.1 вытекает: Следствие 8.1. Множество Теорема 8.3. Произвольное непустое множество Доказательство. Пусть – вопреки тому, что требуется доказать, - множество
Допустим, что данное множеств упорядочено отношением «меньше». Поэтому оно есть непустое подмножество множества Таким образом, допущение, что данное множество не имеет первого элемента, приводит к противоречию. Теорема 8.4. Произвольное множество порядковых чисел, упорядоченное отношением «меньше», есть вполне упорядоченное множество. Доказательство. Непосредственно следует из определения 6.1 и теоремы 8.3. Согласимся обозначать множество всех порядковых чисел, упорядоченное отношением «меньше», символом ПЧ+, а начальный отрезок данного множества, определяемый элементом α – символом ПЧ(α). Таким образом, теорему 8.2 мы можем записать: α Определение 8.2. α Выражение «α Например, предельные числа – это числа Теорема 8.5. α Доказательство. Пусть (1) α а также вопреки тому, что требуется доказать, - (2) Обозначим через α0 наименьшее порядковое число, удовлетворяющее условиям (1) и (2). Существование такого числа гарантируется теоремой 8.3 и принятыми допущениями. Поэтому существует такое порядковое число β0, что (3) α0=β0+1. Если бы β0 Поэтому имеет место соотношение (4) β0 Из (1) и (3) легко следует, что (5) β0 Из формулы (3) и определения 8.1 следует, что β0<α0. Отсюда, из допущения, что α0 – наименьшее порядковое число, удовлетворяющее одновременно условиям (1) и (2), а также из формул (4) и (5) следует существование такого предельного числа β1 и такого натурального числа n1, что β0= β1+ n1. Из этой формулы, формулы (3) и теоремы 3.1а следует: α0= β1+ (n1+1).
Полученная формула противоречит допущению, что α0 удовлетворяет условию (2). Следовательно, исходная формулировка теоремы верна.
Принцип индукции. В этом параграфе ты обобщим принцип индукции, который является законом арифметики натуральных чисел. Принцип индукции формулируется или в качестве арифметической Теоремы, или в качестве правила доказательства теорем. В первой формулировке этот принцип имеет вид: (1) 0 При формулировке принципа индукции в качестве правила используется символ W(n), который обозначает произвольную формулу (или более обще, произвольную теорему), записанную с помощью переменной, пробегающей множество всех натуральных чисел N. Правило индукции мы запишем так же, как мы записывали логические правила в части I:
Пользуясь правилом I, можно доказать теорему (1), и обратно: на основании (1) можно показать, что правило I производно относительно логических правил. В доказательствах математических теорем часто применяется правило, отличное от правила I, называемое, однако, также правилом индукции. Схема этого правила имеет вид:
Арифметическая теорема – аналог правила II в том смысле, в каком теорема (1) есть аналог правила I, – имеет вид: (2) В арифметике натуральных чисел правила I и II эквивалентны. Но только правило II можно распространить на арифметику порядковых чисел вследствие того, что не всякое порядковое число можно получить из нуля прибавлением единицы, в то время как любое натуральное число, очевидно, можно получить таким способом. К порядковым числам, которые нельзя получить из нуля прибавлением единицы, относятся, например, числа w, w+1, w+w, w×w. Схема обобщенного правила индукции имеет вид:
где Для того, чтобы установить, что формула W( Теорема 9.1. Правило индукции, схема которого есть схема III, производно относительно логических правил. Доказательство. Пусть W(
Пусть (1) и далее пусть – вопреки тому, что требуется доказать, - формула W( (2) ~ W( Обозначим через Ф множество всех порядковых чисел, для которых не выполняется формула W( Из (2) следует, что данное множество непусто. Значит, то теореме 8.3 в нём существует наименьшее число Таким образом, имеют место формулы: (3) ~ W( (4) Из формул (1) и (4) следует W( Доказательство, которое мы провели, аналогично доказательству правила II на основании так называемого принципа наименьшего числа, который имеет следующую словесную формулировку: в произвольном непустом множестве натуральных чисел существует наименьший элемент. Обобщением этого принципа является теорема 8.3. Подобно тому как в данном параграфе были обобщены некоторые теоремы арифметики, можно обобщить метод определения, который называется методом определения по индукции и часто применятся в арифметике и других разделах математики.
Здесь мы ограничимся нестрогим описанием определения этого метода. Некоторое свойство, которым обладает каждый предмет данного вполне упорядоченного множества, определяется так: Сначала это свойство определяется для первого элемента рассматриваемого множества, а затем в предположении, что свойство определено уже для всех элементов, предшествующих некоторому произвольному элементу a данного множества, свойство определяется для элемента a. Примером индуктивного определения является определение возведения в степень порядковых чисел: Определение 9.1. a. b. c. В случае, когда Можно обобщить также понятие бесконечной последовательности. Определение 9.2. Трансфинитная последовательность типа В случае Индексы членов последовательности типа α – это порядковые числа меньше числа α. Последовательность типа α обозначается α0, α1, α2, …, αξ, …, где ξ < α или же кратко {αξ}ξ < α Опуская в определении 9.2 условие α ≥ ω, получаем наиболее общее понятие последовательности, также содержащее в качестве частного случая понятие бесконечной последовательности. Последовательности часто определяются интуитивно. §10.Теорема Цермело. Альфы. Гипотеза континуума.
Следующая важная и имеющая применение во многих математики теорема называется теоремой Цермело. Теорема 10.1. Для любого множества А существует высшее упорядоченное множество, запас которого есть множество А. Иначе эту теорему можно сформулировать так: Для любого множества А существует также отношение R, что упорядоченная пара <А,R> есть вполне упорядоченное множество. Данную теорему часто формулируют в краткой, но неточной форме: Любое множество можно вполне упорядочить. Доказательство этой теоремы мы опускаем. Определение 10.1.
Это определение корректно, потому что в силу следствия 2.2 множества, порядковые типы которых равны, имеют мощность. Таким образом, символ Из определения 10.1 и следствия 5.2 следует: Следствие 10.1. Определение 10.2. Таким образом, множество Z(m) есть множество всех порядковых чисел, кардинальное число которых равно m. Теорема 10.2. m Доказательство. Из теоремы 7.2с раздела I следует существование множества, удовлетворяющего условию
Из теоремы 10.1 следует существование вполне упорядоченного множества A+ с запасом А. Из теоремы 2.2 в следует существование порядкового числа
Отсюда, а также из определения 10.1 и условия (1) мы получаем, что
Тем самым по определению 10.2 Таким образом, множество Z(m) непусто. Определение 10.3. а. b. Из теорем 10.2 и 8.3 следует: Следствие 10.2. Если m Определение 10.4. Легко видеть, что w – начальное число множества Z( Таким образом, из определения 10.4 и в силу замечания, что нуль есть порядковый тип пустого множества. (1) w=w0. Заметим еще, что начальное число w1 обозначается обычно символом Определение 10.5. m= Кардинальные числа, которые можно обозначать буквой Рассмотрим, согласуется ли смысл символа По определению 10.5 начальное число множества Z( Таким образом, по определениям 10.3а и 10.2 Теорема 10.3. Для любого кардинального числа m m= Иначе эту теорему можно сформулировать так: Любое трансфинитное кардинальное число есть алеф. Доказательство. Пусть По определению 10.4 Таким образом теорема верна. Из определений 10.2, 10.3а, 10.4 и 10.5 легко следует Следствие 10.3. Теорема 10.4. Таким образом, кардинальное число Доказательство. Допустим, что множество
Отсюда и из определения 10.1 мы получаем
Из этой формулы и следствия 10.3 следует теорема. Теорема 10.5. Доказательство. Из определения 10.4 следует, что (1) Из формулы (1) и следствия 9.1 раздела I следует
Отсюда и из теоремы 10.4 следует в свою очередь
Если бы Таким образом, верно только
Теорема 10.6. Доказательство опускаем. Проблемой континуума называется вопрос, равны ли числа áK, Rñ= Заметим, что проблема континуума эквивалентна вопросу, существует ли кардинальное число m, удовлетворяющее неравенству
а тем самым вопросу, существует ли бесконечное и несчетное множество действительных чисел, неравночисленное множеству K. Проблема континиума была сформулирована создателем теории множеств Кантором и до сих пор еще не решена. Известно лишь (К. Гёдель, 1940 г.), что гипотеза континуума не может быть источником противоречий в теории множеств.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 71; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.094 с.) |

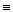
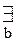 A+
A+ 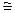 B(b).
B(b).


 если
если 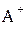 =
= 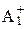 ,
, 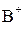 =
= 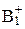 и
и 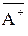 <
< 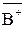 , то
, то 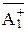 <
< 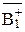 .
.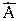 (a) <
(a) < 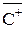
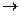 α
α 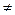 β.
β.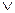 β<α. Эта лемма следует из теоремы 7.2 и определения 8.1.
β<α. Эта лемма следует из теоремы 7.2 и определения 8.1.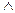 β < γ
β < γ 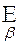 (β < α) упорядочено отношением «меньше», то
(β < α) упорядочено отношением «меньше», то α =
α = 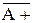
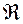 , определяемое эквивалентностью
, определяемое эквивалентностью α
α 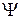 порядковых чисел, упорядоченное отношением «меньше», имеет первый элемент.
порядковых чисел, упорядоченное отношением «меньше», имеет первый элемент.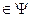
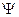 .
.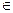 ПЧ+
ПЧ+ 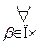 α
α 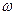 ,
, 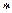
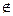 ПрЧ
ПрЧ 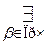
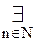 α=β+n.
α=β+n.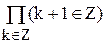
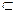 Z
Z I. W(0)
I. W(0) 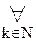 [W(k)
[W(k) 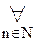 W(n)
W(n) II.
II. 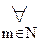 [
[ 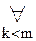 k
k  III.
III. 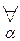 [
[ 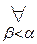 W(β)
W(β) 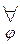 W(
W(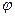 )
)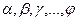 пробегают множество всех порядковых чисел.
пробегают множество всех порядковых чисел. , которая пробегает множество всех порядковых чисел.
, которая пробегает множество всех порядковых чисел.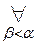 W(β)
W(β) 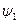 )
)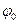 );
);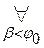 W(β).
W(β).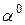 =1.
=1.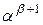 =
= 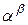
 .
.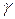
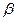 +1, то
+1, то 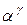 определяется как наименьшее порядковое число, которое больше любого числа
определяется как наименьшее порядковое число, которое больше любого числа 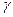 .
.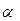 есть функция, левая область которой – множество всех порядковых чисел меньше
есть функция, левая область которой – множество всех порядковых чисел меньше 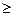 w.
w.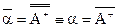
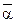 обозначит мощность вполне упорядоченного множества, имеющего порядковое число α. Будем говорить, что
обозначит мощность вполне упорядоченного множества, имеющего порядковое число α. Будем говорить, что 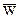 =<
=< 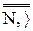 >=
>= 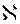 0
0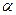
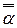 =m.
=m.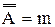
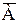 +.
+.
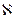 0 и
0 и 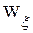 тогда и только тогда, когда
тогда и только тогда, когда 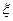 .
. .
.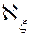 тогда и только тогда, когда начальное число множества Z(m) есть
тогда и только тогда, когда начальное число множества Z(m) есть 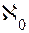 , следующий из определения 10.5, с его прежним смыслом.
, следующий из определения 10.5, с его прежним смыслом.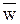 =
= 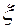 , что
, что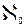 . Обозначим через
. Обозначим через 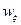 . Отсюда и из определения 10.5 m=
. Отсюда и из определения 10.5 m= 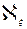 .
.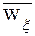 .
.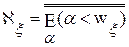 .
.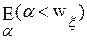 упорядочено отношением «меньше». Из теоремы 8.2 следует поэтому формула:
упорядочено отношением «меньше». Из теоремы 8.2 следует поэтому формула: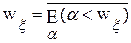
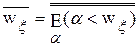
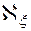 <
< 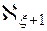
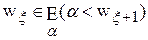 . Отсюда
. Отсюда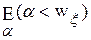
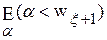
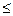
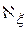 <
< 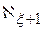 .
.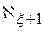 .
.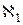
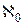 и f или же первое из них меньше второго, а гипотезой континуума называется предположение, что имеет место первая из этих возможностей. Очевидно, что данная гипотеза следует из допущения существования отношения R, вполне упорядочивающего множество K всех действительных чисел, и такого, что
и f или же первое из них меньше второго, а гипотезой континуума называется предположение, что имеет место первая из этих возможностей. Очевидно, что данная гипотеза следует из допущения существования отношения R, вполне упорядочивающего множество K всех действительных чисел, и такого, что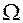 =
=