
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сечения. Плотные и непрерывные множества.
Понятием сечения множеств всех рациональных чисел пользовался Дедекинд, строя арифметику действительных чисел. Определяемое ниже понятие сечения является обобщением понятия, введенного Дедекиндом. Определение 4.1.
Таким образом, сечения – это упорядоченные пары упорядоченных множеств с непустыми и непересекающимися запасами. Множество Ао – нижний класс сечения, Во – высший класс. Из определений 4.1 и 3.1 легко следует, что
Поэтому сечение определяет разбиение всех элементов данного упорядоченного множества на два таких класса, что каждый элемент первого класса предшествует каждому элементу второго класса.
Определение 4.2. а) х есть первый элемент упорядоченного множества
b) х есть последний элемент упорядоченного множества
Определение 4.3. а) Сечение b) Сечение Легко видеть, что любое сечение множества
есть пробел.
2
А В Существуют, очевидно, сечения, которые не являются ним скачками, ни пробелами. К таким сечениям относится, например сечение Определение 4.4. а) Упорядоченное множество плотно тогда, и только тогда, когда ни одно его сечение не есть скачок. b) Упорядоченное множество непрерывно тогда, и только тогда, когда ни одно его сечение не есть ни скачок, ни пробел. Множество áN,<ñ не является, очевидно, ни плотным, ни непрерывным. Множество всех рациональных чисел, упорядоченное отношением «меньше», плотно, но не непрерывно, потому что, как следует из приведенного выше примера, существуют его сечения, являющиеся пробелами.
Однако, множество áÂ,<ñ непрерывно. ( - действительные числа: pÎÂ, Введем понятие включения для упорядоченных множеств, которым мы в дальнейшем будем пользоваться: Определение 4.5. Таким образом, множество Ао включается (содержится) в упорядоченное(м) множество(е) Во тогда, и только тогда, когда запас первого из этих множеств включается (содержится) в смысле установленном в алгебре множеств – в запасе второго и когда элементы множества Ао упорядочены в нем так же, как и в множестве Во. Тем самым символ «Ì» имеет два смысла. Но это не грозит путаницей, потому что обозначения аргументов этого символа будет всегда указываться в каком смысле он употребляется. Заметим, что если АоÌВо,то множество Ао называется частью,или подмножеством множества Во. Из определений 4.5 и 4.1 непосредственно следует: Следствие 4.1. а) b) Теорема 4.1. Таким образом, отношение включения упорядоченных множеств, как и отношение включения неупорядоченных множеств, транзитивно. Доказательство. (1) (2) (3) (1.1) (1.2) (1.3) (1.4) (1.5) Теорема 4.2. а) Если Ао@Во и существует первый элемент множества Ао, то существует и первый элемент множества Во; b) Если Ао@Во и существует последний элемент множества Ао, то существует и последний элемент множества Во; с) Если Ао@Во и множество Ао плотно, то плотно и множество Во; d) Если Ао@Во и множества Ао непрерывно, то непрерывно и множество Во. Доказательство. Эта теорема – непосредственное следствие основной теоремы об изоморфизме, сформированный в §1. Однако это доказательство теории является трудным. Потому мы проводим доказательство теорем 4.2а, b, с, d, не опирающиеся на основную теорему об изоморфизме; эти доказательства не представляют трудностей.
Докажем сначала часть а) теоремы. Допустим, что взаимооднозначное отношение R устанавливает подобие множеств Ао и Во, а также, что а1 – первый элемент множества Ао. Покажем, что b1=R(а1) – первый элемент множества Во. В самом деле, если бы существовал такой элемент b2 множества Во, что Таким образом, элемент а1 не был бы – вопреки условию – первым элементом множества Ао. Доказательство части b) теоремы аналогично. Докажем теперь часть c) теоремы. Допустим вновь, что взаимооднозначное отношение R устанавливает подобие множеств Ао и Во, а также, что множество Ао плотно. Допустим также – вопреки тому, что мы хотим доказать, - что некоторое сечение
Легко выдать, что Доказательство части a теории аналогично. Теорема 4.3. Упорядоченное множество А0 плотно
________________________ * – выражение
Доказательство. Допустим вначале, что множество Ао плотно, и пусть х и у – его произвольные элементы, удовлетворяющие условию (1) Пусть подмножества Хо и Yо множества Ао удовлетворяют условиям (2) (3) Если бы не существовало элемента Z, удовлетворяющего условию (4) то как легко видеть – упорядоченная пара Значит, из этого допущения следует, что для любых двух элементов х, у множества Ао, удовлетворяющих условию (1), существует элемент, удовлетворяющий условию (4). Допустим теперь, что множество Ао не плотно. Поэтому существует сечение Если бы некоторый элемент z множества Ао удовлетворял бы условию (4), то этот элемент не принадлежал бы ни множеству Хо, ни множеству Yо и упорядоченная пара Тем самым доказательство теоремы закончено.
|
||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 89; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.252 (0.022 с.) |
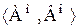 есть сечение упорядоченного множества;
есть сечение упорядоченного множества;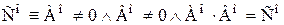



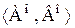 есть скачок тогда, и только тогда, когда существует последний элемент множества Ао и первый элемент множества Во.
есть скачок тогда, и только тогда, когда существует последний элемент множества Ао и первый элемент множества Во. – скачок. Можно показать ниже, что сечение
– скачок. Можно показать ниже, что сечение  ,
, 




 х
х
 х2<2 х2>2
х2<2 х2>2 ÎÂ).
ÎÂ).


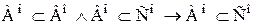 .
.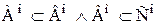
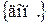

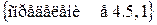


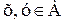
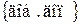



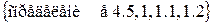

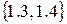



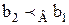 , то существовал бы также и элемент а2 множества Ао, удостоверяющий условию b2=R(а2); причем по определению 2.4 имела бы место эквивалентность
, то существовал бы также и элемент а2 множества Ао, удостоверяющий условию b2=R(а2); причем по определению 2.4 имела бы место эквивалентность 
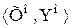 множества Во – скачок. Обозначим через Zо и Uо подмножества множества Ао, удовлетворяющие условиям
множества Во – скачок. Обозначим через Zо и Uо подмножества множества Ао, удовлетворяющие условиям ,
, 
 ,
,  и что упорядоченная пара
и что упорядоченная пара 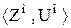 - сечение множества Ао. Поэтому из допущения, что сечение
- сечение множества Ао. Поэтому из допущения, что сечение 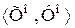 - скачок, из теоремы 4.2а, b следует, что в в множества Zо имеется последний элемент, а в множества Uо – первый элемент. Поэтому сечение
- скачок, из теоремы 4.2а, b следует, что в в множества Zо имеется последний элемент, а в множества Uо – первый элемент. Поэтому сечение 
 - конъюнкция выражений
- конъюнкция выражений 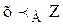 и
и 

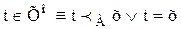 ;
; ;
; ,
, была бы сечение множества, и притом скачком. Это заключение, однако, противоречит допущению, что множество Ао плотно.
была бы сечение множества, и притом скачком. Это заключение, однако, противоречит допущению, что множество Ао плотно.


