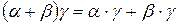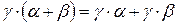Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметика порядковых типов.
Следующие два определения раскрывают содержание понятий суммы и произведения упорядоченных множеств. Определение 3.1.
Определение 3.2.
Легко видеть, что условие:
определяет отношение R1, которое упорядочивает множество А+В, если только А·В=0. Сходным образом условие
определяет отношение S1, которое упорядочивает множество А·В. Таким образом, сумма и произведение упорядоченных множеств являются упорядоченными множествами. Заметим далее, что отношение R упорядочивает множество А+В так, что прежде всего идут все элементы множества Ао в неизменном порядке, а за ними – все элементы множества Во также в неизменном порядке.Пусть множества Ао и Во – множества всех действительных чисел, упорядоченных отношением «меньше». Таким образом, имеют место следующие равенства: Ао=Во=áN,<ñ. Тем самым элементы множества А·В можем рассматривать как точки плоскости, на которой выбрана система координат. Легко видеть, что эти точки упорядочены так, что из двух точек, лежащих на различных горизонтальных прямых (см. рисунок), предшествующей является та точка, которая лежит на прямой, расположенной ниже, а из двух точек, лежащих на одной и той же прямой, предшествующей будет точка, расположенная левее.
Отмеченные на рисунке точки поэтому упорядочены следующим образом: Следующая лемма аналогична лемме 7.5а в разделе I: Лемма 3.1. а) b) Доказательство. Мы приведем лишь доказательства части b) леммы, потому что доказательство части а) аналогично доказательству леммы 7.5а раздела I. Допустим, что отношение R устанавливает подобие множеств Ао и Во, а отношение R1 – подобие множеств Ао1 и Во1. легко видеть, что отношение S, определяемое эквивалентностью
множеств Ао1 и Во1. легко видеть, что отношение S, определяемое эквивалентностью Определим теперь сумму и произведение порядковых типов:
Определение 3.3. Определение 3.4. Заметим, что определений 3.3 и 3.4 мы могли бы более точно записать так:
Покажем, что определение 3.3 корректно. Для этого нужно доказать, что для любых двух порядковых типов a и b существует только один порядковый тип, равный их сумме. По теореме 2.2с существуют упорядоченные множества Ао и Во, такие что
На основании леммы 2.1 можем допустить, что Отсюда в свою очередь мы получаем на основании аксиомы 2.1 и определения 3.3:
Таким образом, может существовать лишь одна сумма двух данных порядковых типов. То, что такая сумма всегда существует, следует из леммы 2.1, определения 3.3, теоремы 2.2b и замечания о том, что сумма двух упорядоченных множеств есть упорядоченное множество. Сходным образом можно показать корректность D 3.4 Теорема 3.1. а) (a+b)+g=a+(b+g) b) (a·b)·g=a·(b·g) Таким образом, сложение и умножение порядковых номеров ассоциативно. Однако эти операции, как мы убедимся ниже, некоммуникативны, то есть Доказательство. Докажем лишь формулу а). Пусть Ао, Во, Со – упорядоченные множества, удовлетворяющие условиям: (1) Существование таких множеств гарантирует теорема 2.2с. На основании леммы 2.1 мы можем допустить, что (2) А·В=А·С=В·С=0 Введем обозначения: (3) Dо=Ао+Во, Ео=Во+Со; Хо=(Ао+Во)+Со, Yо=Ао+(Во+Со) Из определения 3.1, (2) и (3) следуют равенства: Х = (А+В)+С, Y=А+(В+С) Отсюда: (4) Х=Y Из определения 3.1, (2) и (3) следует ниже равенство:
Отсюда: (5) Из определения 2.4, а также из (4) и (5) следует, что отношение тождества, ограниченное множеством Х, устанавливает подобие множеств Хо и Yо. Отсюда, из определения 2.5 и аксиомы 2.1 следует (6) C другой стороны, из определения 3.3, (2) и (3) следует равенство:
Из этих равенств, а также из формул (6) и (1) следует формула а). Приведем еще следующую теорему: Теорема 3.2. а) b) Таким образом, умножение порядковых типов дистрибутивно относительно сложения. Некоммуникативность умножения порядковых типов приводит к тому, что фигурируют два закона дистрибутивности.
Доказательство теоремы 3.2 опускаем.
|
||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 79; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.18.220.243 (0.011 с.) |
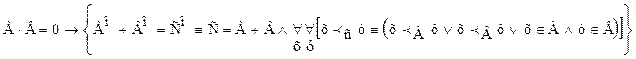
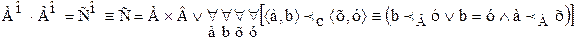
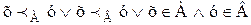
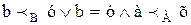


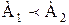
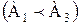

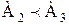
 ½
½ 
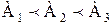
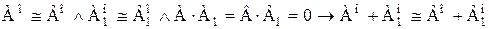
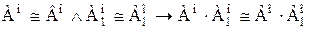
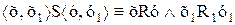
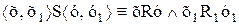 устанавливает подобие множеств Ао·Ао1 и Во·Во1.
устанавливает подобие множеств Ао·Ао1 и Во·Во1.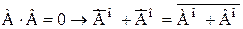
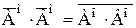
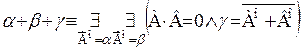
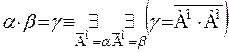
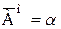 и
и 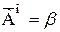 Пусть
Пусть 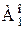 и
и 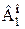 – произвольные упорядоченные множества, удовлетворяющее условиям:
– произвольные упорядоченные множества, удовлетворяющее условиям: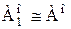 ,
, 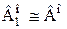 .
.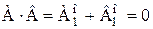 . Отсюда и из леммы 3.1 следует, что
. Отсюда и из леммы 3.1 следует, что 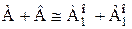 .
.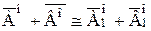
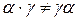 ,
, 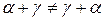
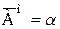 ,
, 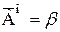 ,
, 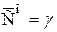
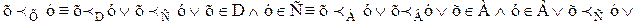
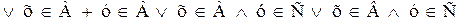 ;
;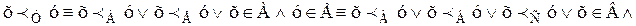
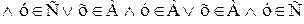 .
.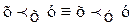
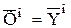
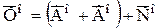 ,
,